[Updated on 2020-01-09: add a new section on Contrastive Predictive Coding].
[Updated on 2020-04-13: add a “Momentum Contrast” section on MoCo, SimCLR and CURL.]
[Updated on 2020-07-08: add a “Bisimulation” section on DeepMDP and DBC.]
[Updated on 2020-09-12: add MoCo V2 and BYOL in the “Momentum Contrast” section.]
[Updated on 2021-05-31: remove section on “Momentum Contrast” and add a pointer to a full post on “Contrastive Representation Learning”]
Given a task and enough labels, supervised learning can solve it really well. Good performance usually requires a decent amount of labels, but collecting manual labels is expensive (i.e. ImageNet) and hard to be scaled up. Considering the amount of unlabelled data (e.g. free text, all the images on the Internet) is substantially more than a limited number of human curated labelled datasets, it is kinda wasteful not to use them. However, unsupervised learning is not easy and usually works much less efficiently than supervised learning.
What if we can get labels for free for unlabelled data and train unsupervised dataset in a supervised manner? We can achieve this by framing a supervised learning task in a special form to predict only a subset of information using the rest. In this way, all the information needed, both inputs and labels, has been provided. This is known as self-supervised learning.
This idea has been widely used in language modeling. The default task for a language model is to predict the next word given the past sequence. BERT adds two other auxiliary tasks and both rely on self-generated labels.
Here is a nicely curated list of papers in self-supervised learning. Please check it out if you are interested in reading more in depth.
Note that this post does not focus on either NLP / language modeling or generative modeling.
Why Self-Supervised Learning?
Self-supervised learning empowers us to exploit a variety of labels that come with the data for free. The motivation is quite straightforward. Producing a dataset with clean labels is expensive but unlabeled data is being generated all the time. To make use of this much larger amount of unlabeled data, one way is to set the learning objectives properly so as to get supervision from the data itself.
The self-supervised task, also known as pretext task, guides us to a supervised loss function. However, we usually don’t care about the final performance of this invented task. Rather we are interested in the learned intermediate representation with the expectation that this representation can carry good semantic or structural meanings and can be beneficial to a variety of practical downstream tasks.
For example, we might rotate images at random and train a model to predict how each input image is rotated. The rotation prediction task is made-up, so the actual accuracy is unimportant, like how we treat auxiliary tasks. But we expect the model to learn high-quality latent variables for real-world tasks, such as constructing an object recognition classifier with very few labeled samples.
Broadly speaking, all the generative models can be considered as self-supervised, but with different goals: Generative models focus on creating diverse and realistic images, while self-supervised representation learning care about producing good features generally helpful for many tasks. Generative modeling is not the focus of this post, but feel free to check my previous posts.
Images-Based
Many ideas have been proposed for self-supervised representation learning on images. A common workflow is to train a model on one or multiple pretext tasks with unlabelled images and then use one intermediate feature layer of this model to feed a multinomial logistic regression classifier on ImageNet classification. The final classification accuracy quantifies how good the learned representation is.
Recently, some researchers proposed to train supervised learning on labelled data and self-supervised pretext tasks on unlabelled data simultaneously with shared weights, like in Zhai et al, 2019 and Sun et al, 2019.
Distortion
We expect small distortion on an image does not modify its original semantic meaning or geometric forms. Slightly distorted images are considered the same as original and thus the learned features are expected to be invariant to distortion.
Exemplar-CNN (Dosovitskiy et al., 2015) create surrogate training datasets with unlabeled image patches:
- Sample $N$ patches of size 32 × 32 pixels from different images at varying positions and scales, only from regions containing considerable gradients as those areas cover edges and tend to contain objects or parts of objects. They are “exemplary” patches.
- Each patch is distorted by applying a variety of random transformations (i.e., translation, rotation, scaling, etc.). All the resulting distorted patches are considered to belong to the same surrogate class.
- The pretext task is to discriminate between a set of surrogate classes. We can arbitrarily create as many surrogate classes as we want.

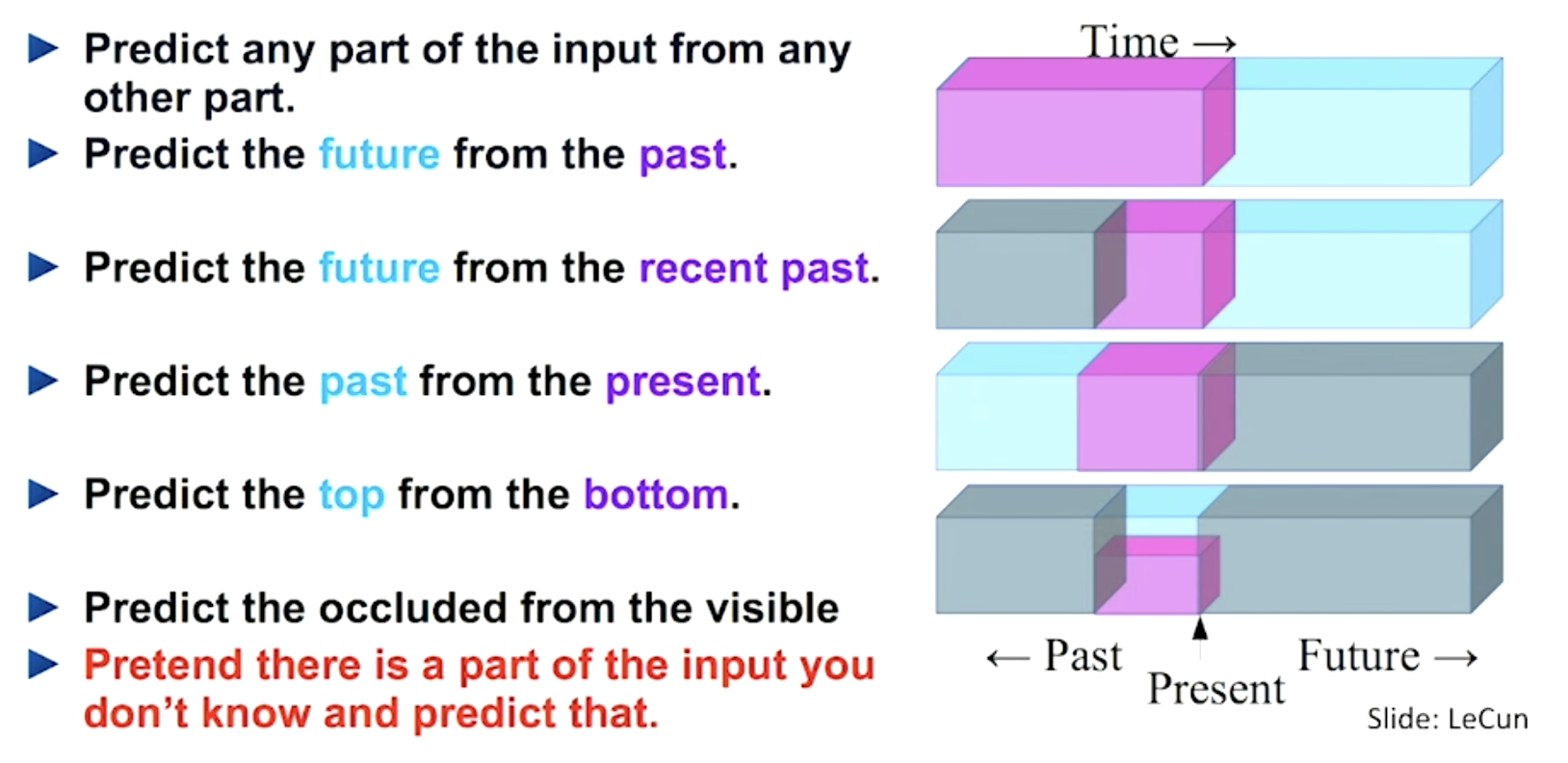
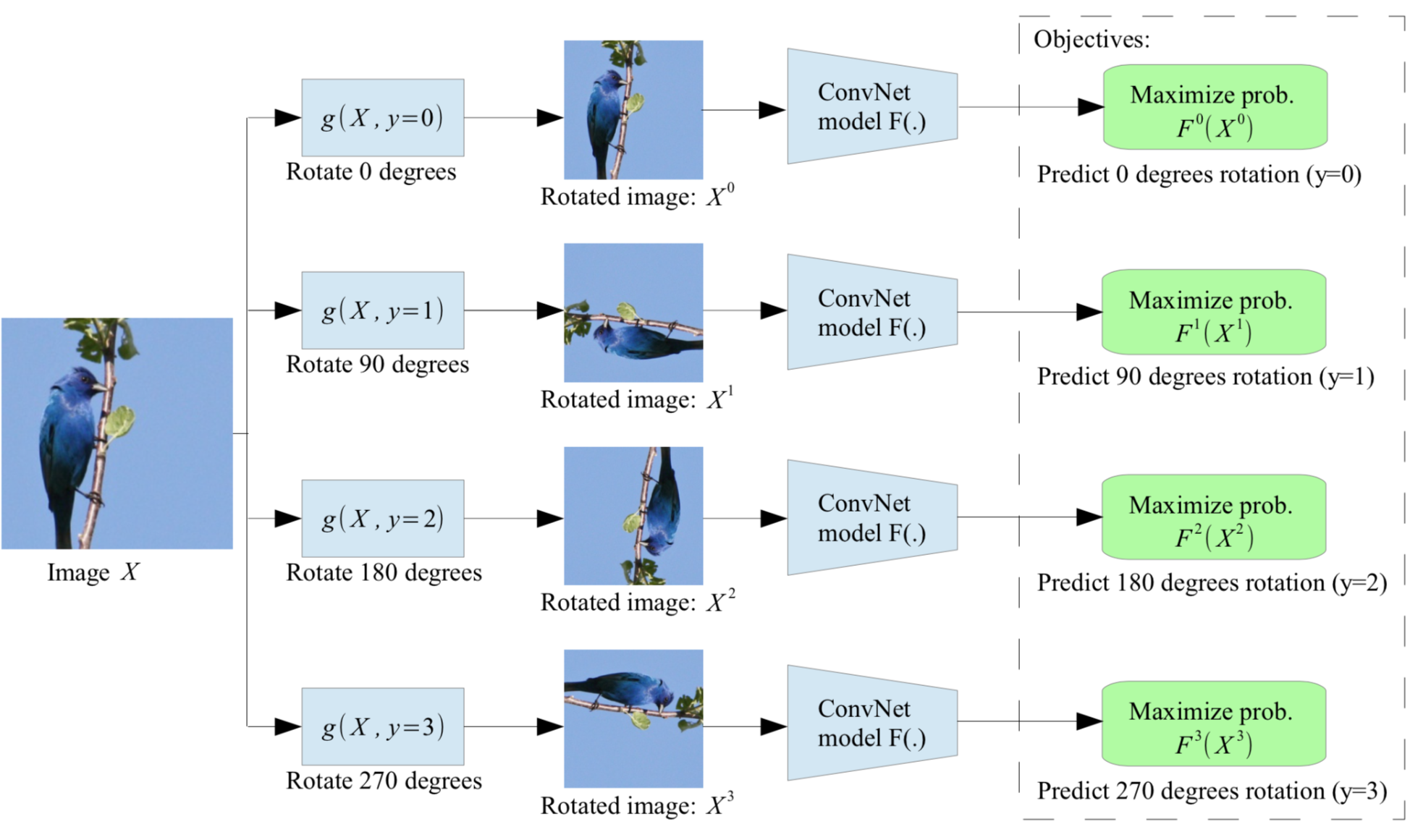
Rotation of an entire image (Gidaris et al. 2018 is another interesting and cheap way to modify an input image while the semantic content stays unchanged. Each input image is first rotated by a multiple of $90^\circ$ at random, corresponding to $[0^\circ, 90^\circ, 180^\circ, 270^\circ]$. The model is trained to predict which rotation has been applied, thus a 4-class classification problem.
In order to identify the same image with different rotations, the model has to learn to recognize high level object parts, such as heads, noses, and eyes, and the relative positions of these parts, rather than local patterns. This pretext task drives the model to learn semantic concepts of objects in this way.
Patches
The second category of self-supervised learning tasks extract multiple patches from one image and ask the model to predict the relationship between these patches.
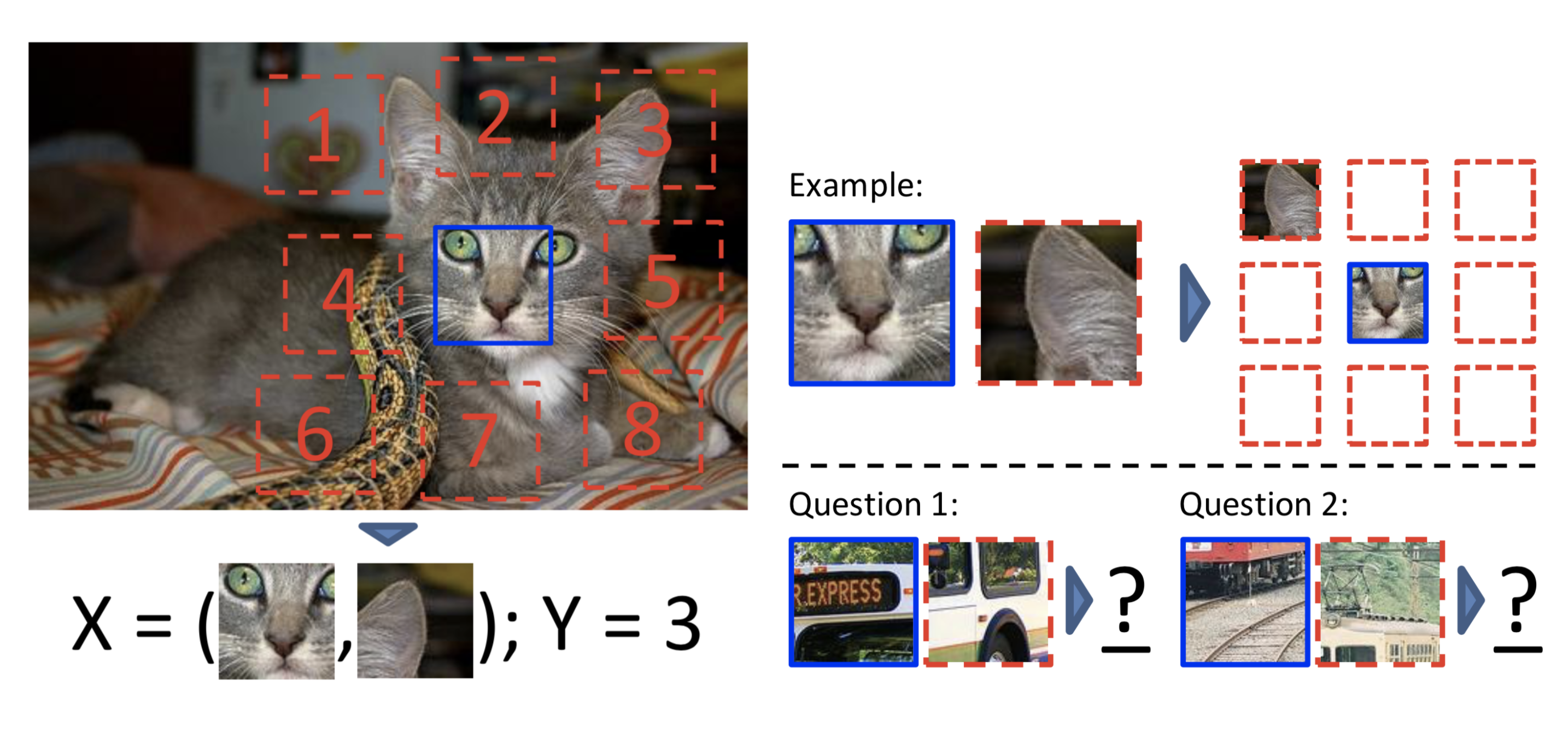
Doersch et al. (2015) formulates the pretext task as predicting the relative position between two random patches from one image. A model needs to understand the spatial context of objects in order to tell the relative position between parts.
The training patches are sampled in the following way:
- Randomly sample the first patch without any reference to image content.
- Considering that the first patch is placed in the middle of a 3x3 grid, and the second patch is sampled from its 8 neighboring locations around it.
- To avoid the model only catching low-level trivial signals, such as connecting a straight line across boundary or matching local patterns, additional noise is introduced by:
- Add gaps between patches
- Small jitters
- Randomly downsample some patches to as little as 100 total pixels, and then upsampling it, to build robustness to pixelation.
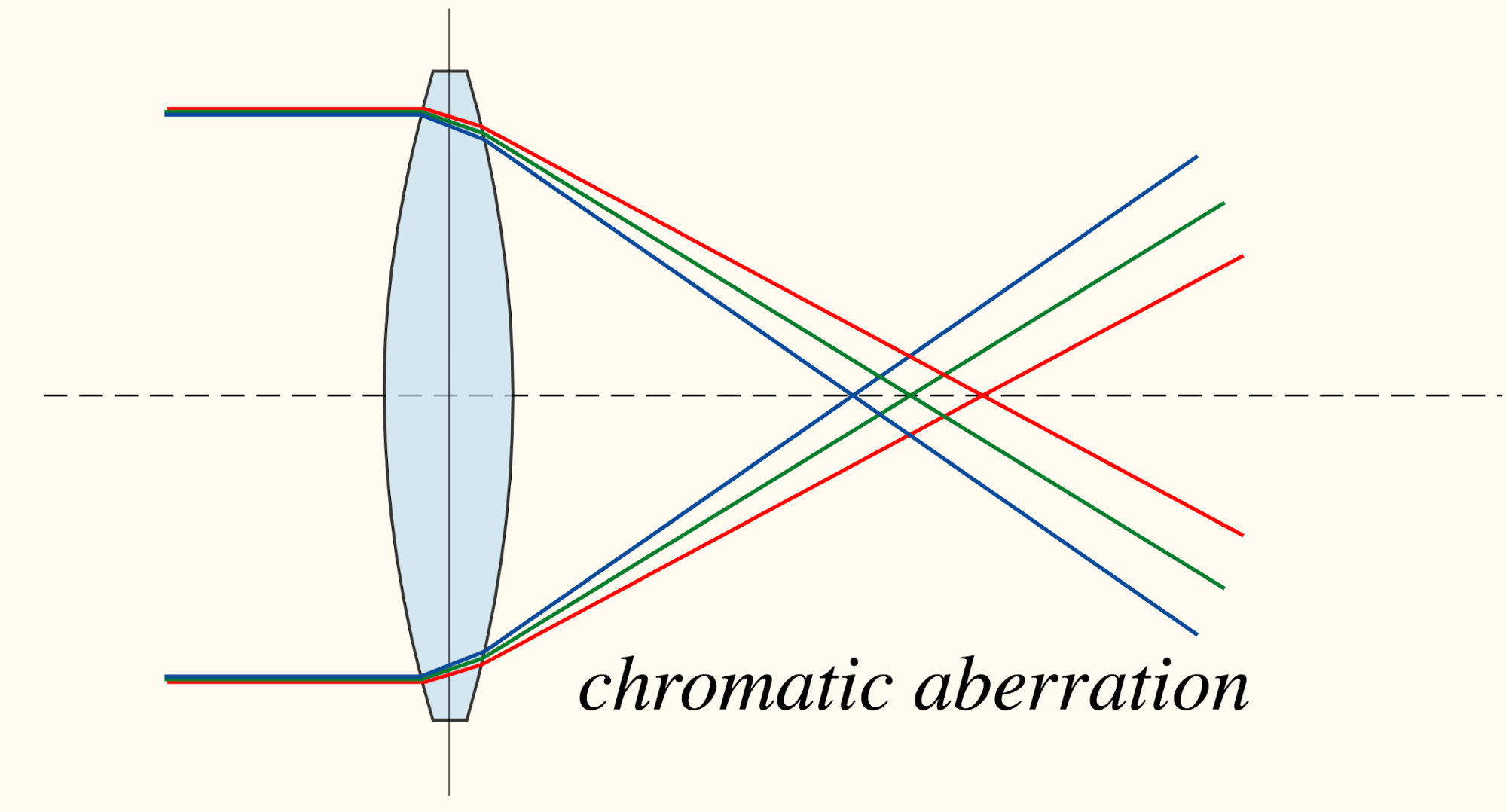
- Shift green and magenta toward gray or randomly drop 2 of 3 color channels (See “chromatic aberration” below)
- The model is trained to predict which one of 8 neighboring locations the second patch is selected from, a classification problem over 8 classes.
Other than trivial signals like boundary patterns or textures continuing, another interesting and a bit surprising trivial solution was found, called “chromatic aberration”. It is triggered by different focal lengths of lights at different wavelengths passing through the lens. In the process, there might exist small offsets between color channels. Hence, the model can learn to tell the relative position by simply comparing how green and magenta are separated differently in two patches. This is a trivial solution and has nothing to do with the image content. Pre-processing images by shifting green and magenta toward gray or randomly dropping 2 of 3 color channels can avoid this trivial solution.
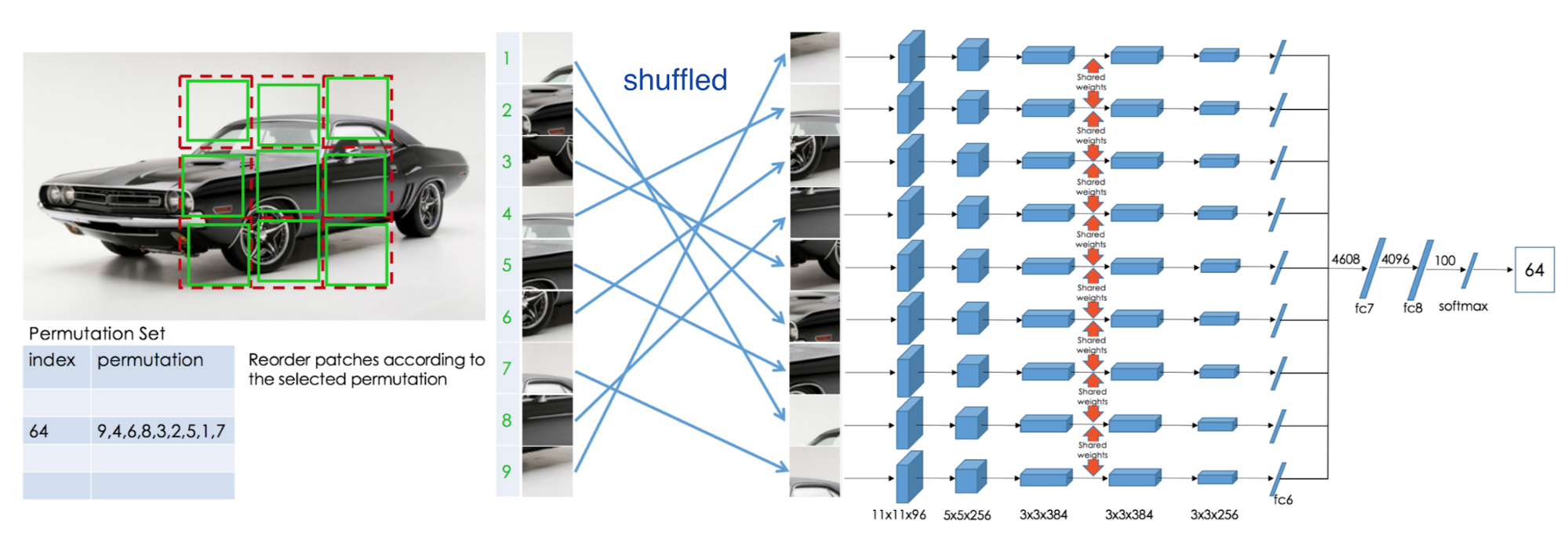
Since we have already set up a 3x3 grid in each image in the above task, why not use all of 9 patches rather than only 2 to make the task more difficult? Following this idea, Noroozi & Favaro (2016) designed a jigsaw puzzle game as pretext task: The model is trained to place 9 shuffled patches back to the original locations.
A convolutional network processes each patch independently with shared weights and outputs a probability vector per patch index out of a predefined set of permutations. To control the difficulty of jigsaw puzzles, the paper proposed to shuffle patches according to a predefined permutation set and configured the model to predict a probability vector over all the indices in the set.
Because how the input patches are shuffled does not alter the correct order to predict. A potential improvement to speed up training is to use permutation-invariant graph convolutional network (GCN) so that we don’t have to shuffle the same set of patches multiple times, same idea as in this paper.
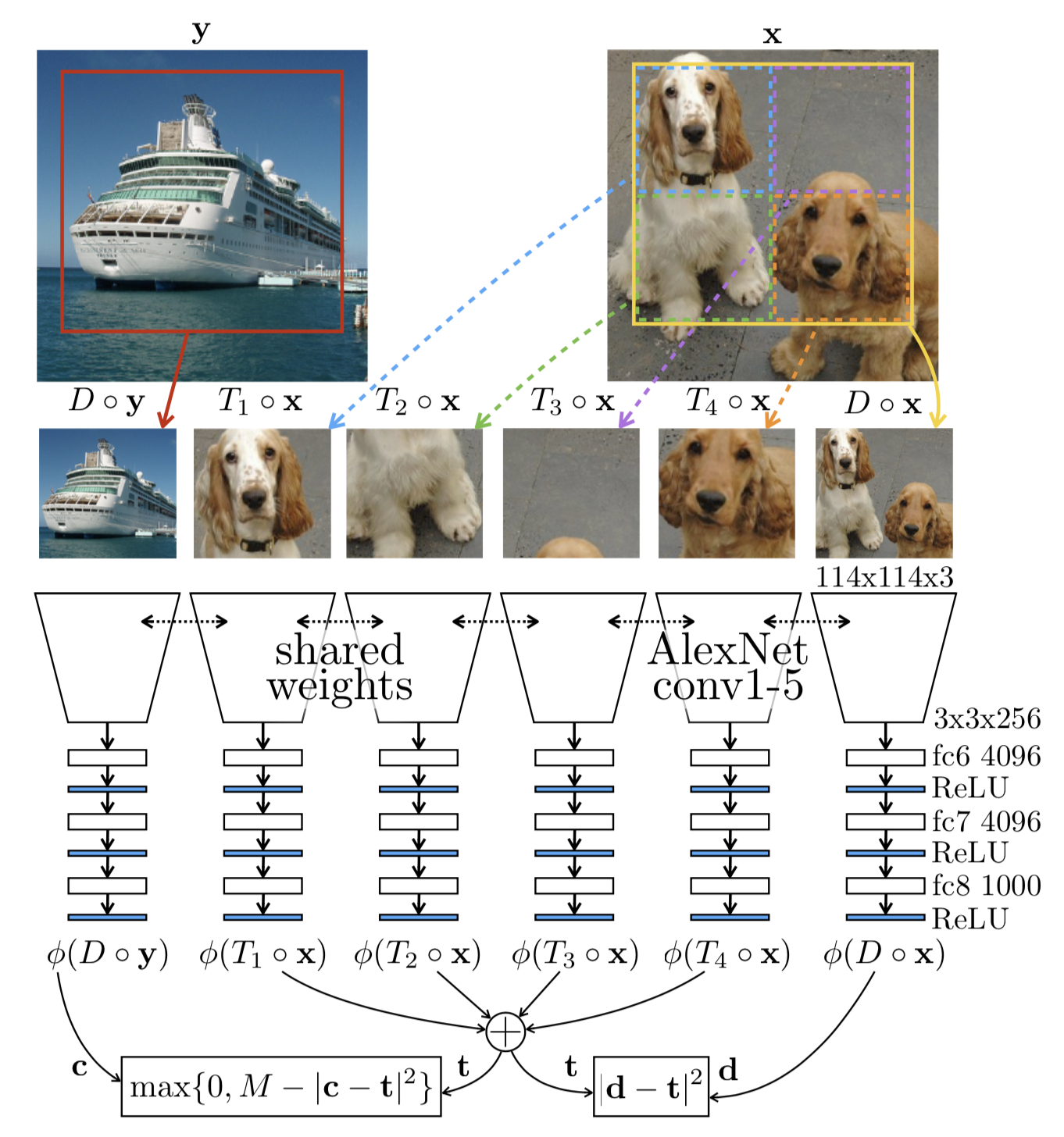
Another idea is to consider “feature” or “visual primitives” as a scalar-value attribute that can be summed up over multiple patches and compared across different patches. Then the relationship between patches can be defined by counting features and simple arithmetic (Noroozi, et al, 2017).
The paper considers two transformations:
- Scaling: If an image is scaled up by 2x, the number of visual primitives should stay the same.
- Tiling: If an image is tiled into a 2x2 grid, the number of visual primitives is expected to be the sum, 4 times the original feature counts.
The model learns a feature encoder $\phi(.)$ using the above feature counting relationship. Given an input image $\mathbf{x} \in \mathbb{R}^{m \times n \times 3}$, considering two types of transformation operators:
- Downsampling operator, $D: \mathbb{R}^{m \times n \times 3} \mapsto \mathbb{R}^{\frac{m}{2} \times \frac{n}{2} \times 3}$: downsample by a factor of 2
- Tiling operator $T_i: \mathbb{R}^{m \times n \times 3} \mapsto \mathbb{R}^{\frac{m}{2} \times \frac{n}{2} \times 3}$: extract the $i$-th tile from a 2x2 grid of the image.
We expect to learn:
Thus the MSE loss is: $\mathcal{L}_\text{feat} = |\phi(D \circ \mathbf{x}) - \sum_{i=1}^4 \phi(T_i \circ \mathbf{x})|^2_2$. To avoid trivial solution $\phi(\mathbf{x}) = \mathbf{0}, \forall{\mathbf{x}}$, another loss term is added to encourage the difference between features of two different images: $\mathcal{L}_\text{diff} = \max(0, c -|\phi(D \circ \mathbf{y}) - \sum_{i=1}^4 \phi(T_i \circ \mathbf{x})|^2_2)$, where $\mathbf{y}$ is another input image different from $\mathbf{x}$ and $c$ is a scalar constant. The final loss is:
Colorization
Colorization can be used as a powerful self-supervised task: a model is trained to color a grayscale input image; precisely the task is to map this image to a distribution over quantized color value outputs (Zhang et al. 2016).
The model outputs colors in the the CIE Lab* color space. The Lab* color is designed to approximate human vision, while, in contrast, RGB or CMYK models the color output of physical devices.
- L* component matches human perception of lightness; L* = 0 is black and L* = 100 indicates white.
- a* component represents green (negative) / magenta (positive) value.
- b* component models blue (negative) /yellow (positive) value.
Due to the multimodal nature of the colorization problem, cross-entropy loss of predicted probability distribution over binned color values works better than L2 loss of the raw color values. The ab color space is quantized with bucket size 10.
To balance between common colors (usually low ab values, of common backgrounds like clouds, walls, and dirt) and rare colors (which are likely associated with key objects in the image), the loss function is rebalanced with a weighting term that boosts the loss of infrequent color buckets. This is just like why we need both tf and idf for scoring words in information retrieval model. The weighting term is constructed as: (1-λ) * Gaussian-kernel-smoothed empirical probability distribution + λ * a uniform distribution, where both distributions are over the quantized ab color space.
Generative Modeling
The pretext task in generative modeling is to reconstruct the original input while learning meaningful latent representation.
The denoising autoencoder (Vincent, et al, 2008) learns to recover an image from a version that is partially corrupted or has random noise. The design is inspired by the fact that humans can easily recognize objects in pictures even with noise, indicating that key visual features can be extracted and separated from noise. See my old post.
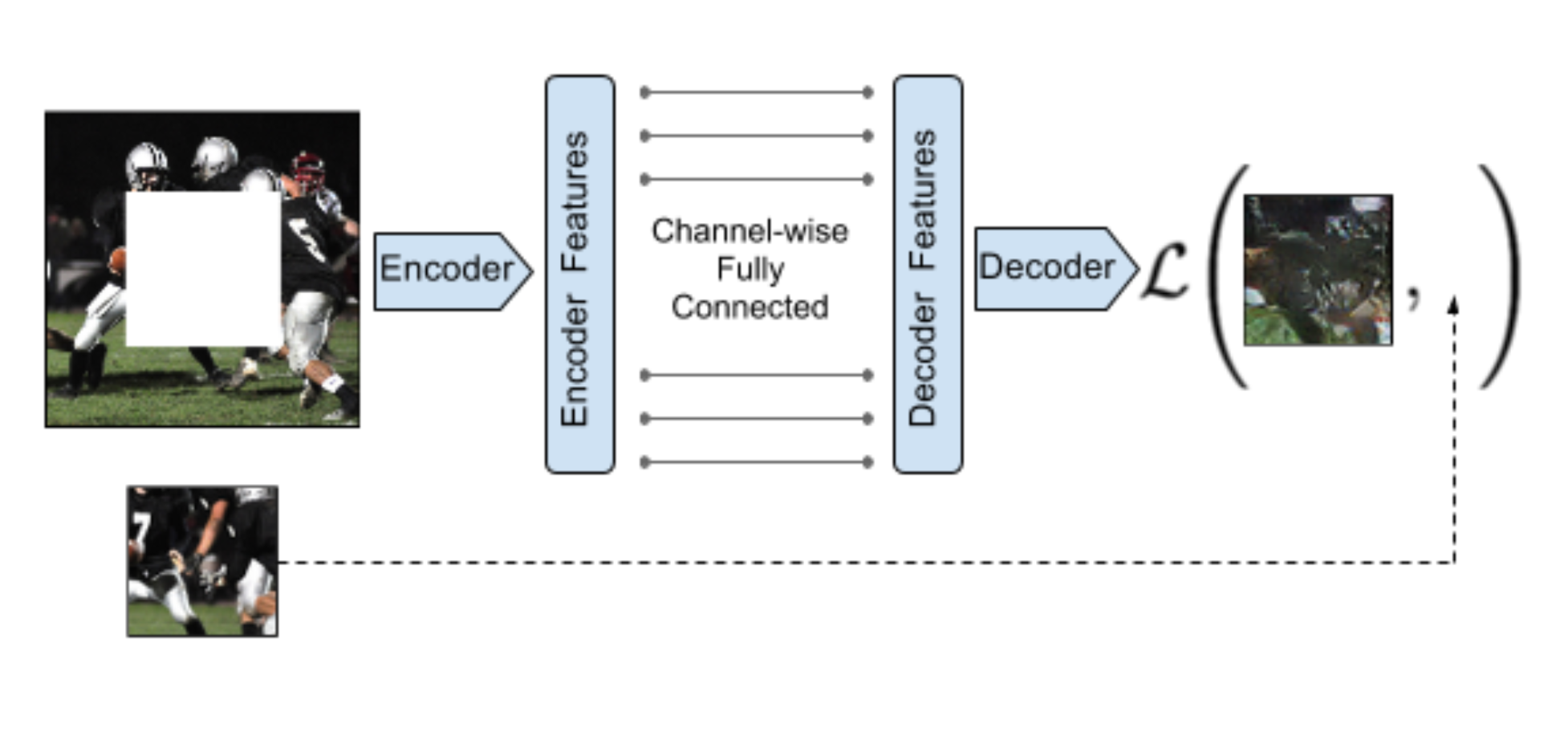
The context encoder (Pathak, et al., 2016) is trained to fill in a missing piece in the image. Let $\hat{M}$ be a binary mask, 0 for dropped pixels and 1 for remaining input pixels. The model is trained with a combination of the reconstruction (L2) loss and the adversarial loss. The removed regions defined by the mask could be of any shape.
where $F(.)$ is the full pipeline of reconstructing the input image with missing regions via impainting, including both encoder and decoder portions in $D(.)$ is the discriminator model jointly trained, like in GAN.
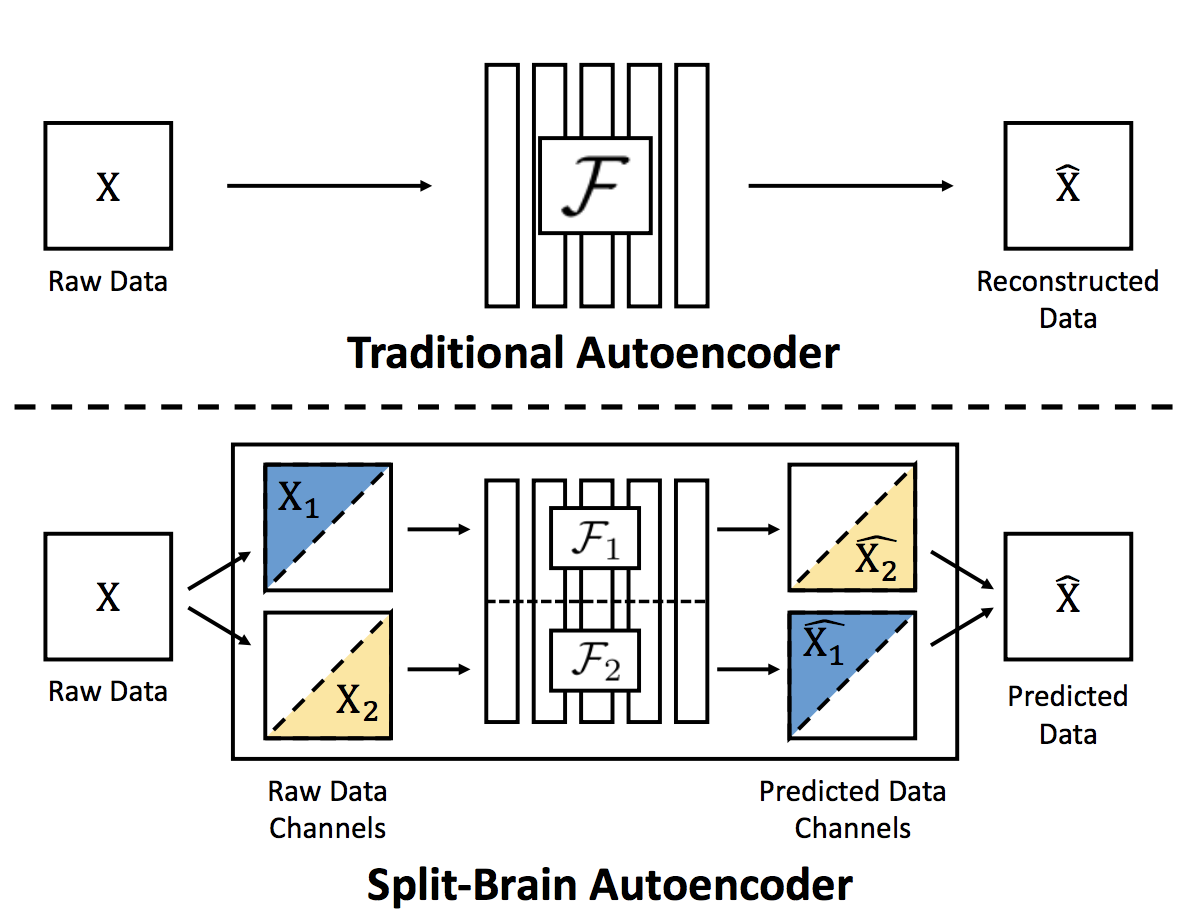
When applying a mask on an image, the context encoder removes information of all the color channels in partial regions. How about only hiding a subset of channels? The split-brain autoencoder (Zhang et al., 2017) does this by predicting a subset of color channels from the rest of channels. Let the data tensor $\mathbf{x} \in \mathbb{R}^{h \times w \times \vert C \vert }$ with $C$ color channels be the input for the $l$-th layer of the network. It is split into two disjoint parts, $\mathbf{x}_1 \in \mathbb{R}^{h \times w \times \vert C_1 \vert}$ and $\mathbf{x}_2 \in \mathbb{R}^{h \times w \times \vert C_2 \vert}$, where $C_1 , C_2 \subseteq C$. Then two sub-networks are trained to do two complementary predictions: one network $f_1$ predicts $\mathbf{x}_2$ from $\mathbf{x}_1$ and the other network $f_1$ predicts $\mathbf{x}_1$ from $\mathbf{x}_2$. The loss is either L1 loss or cross entropy if color values are quantized.
The split can happen once on the RGB-D or Lab* colorspace, or happen even in every layer of a CNN network in which the number of channels can be arbitrary.
The generative adversarial networks (GANs) are able to learn to map from simple latent variables to arbitrarily complex data distributions. Studies have shown that the latent space of such generative models captures semantic variation in the data; e.g. when training GAN models on human faces, some latent variables are associated with facial expression, glasses, gender, etc (Radford et al., 2016).
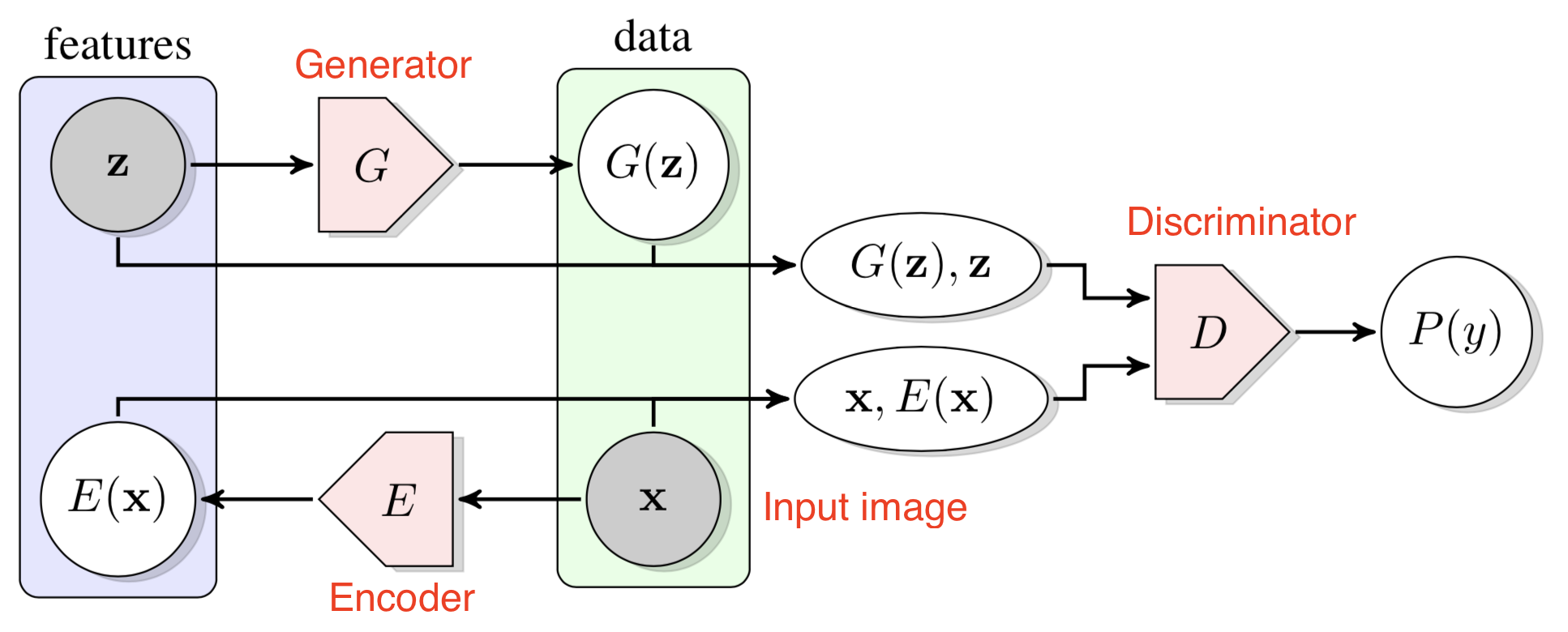
Bidirectional GANs (Donahue, et al, 2017) introduces an additional encoder $E(.)$ to learn the mappings from the input to the latent variable $\mathbf{z}$. The discriminator $D(.)$ predicts in the joint space of the input data and latent representation, $(\mathbf{x}, \mathbf{z})$, to tell apart the generated pair $(\mathbf{x}, E(\mathbf{x}))$ from the real one $(G(\mathbf{z}), \mathbf{z})$. The model is trained to optimize the objective: $\min_{G, E} \max_D V(D, E, G)$, where the generator $G$ and the encoder $E$ learn to generate data and latent variables that are realistic enough to confuse the discriminator and at the same time the discriminator $D$ tries to differentiate real and generated data.
Contrastive Learning
The Contrastive Predictive Coding (CPC) (van den Oord, et al. 2018) is an approach for unsupervised learning from high-dimensional data by translating a generative modeling problem to a classification problem. The contrastive loss or InfoNCE loss in CPC, inspired by Noise Contrastive Estimation (NCE), uses cross-entropy loss to measure how well the model can classify the “future” representation amongst a set of unrelated “negative” samples. Such design is partially motivated by the fact that the unimodal loss like MSE has no enough capacity but learning a full generative model could be too expensive.
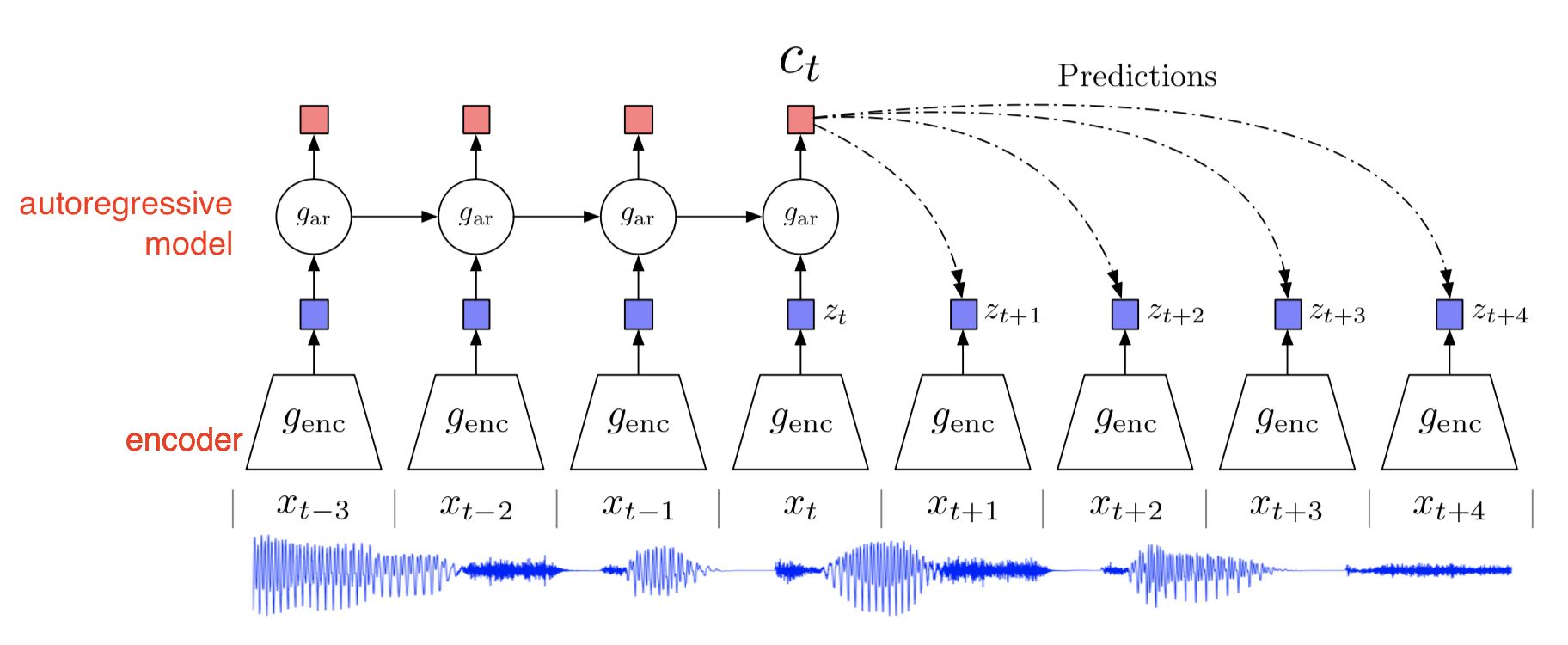
CPC uses an encoder to compress the input data $z_t = g_\text{enc}(x_t)$ and an autoregressive decoder to learn the high-level context that is potentially shared across future predictions, $c_t = g_\text{ar}(z_{\leq t})$. The end-to-end training relies on the NCE-inspired contrastive loss.
While predicting future information, CPC is optimized to maximize the the mutual information between input $x$ and context vector $c$:
Rather than modeling the future observations $p_k(x_{t+k} \vert c_t)$ directly (which could be fairly expensive), CPC models a density function to preserve the mutual information between $x_{t+k}$ and $c_t$:
where $f_k$ can be unnormalized and a linear transformation $W_k^\top c_t$ is used for the prediction with a different $W_k$ matrix for every step $k$.
Given a set of $N$ random samples $X = \{x_1, \dots, x_N\}$ containing only one positive sample $x_t \sim p(x_{t+k} \vert c_t)$ and $N-1$ negative samples $x_{i \neq t} \sim p(x_{t+k})$, the cross-entropy loss for classifying the positive sample (where $\frac{f_k}{\sum f_k}$ is the prediction) correctly is:
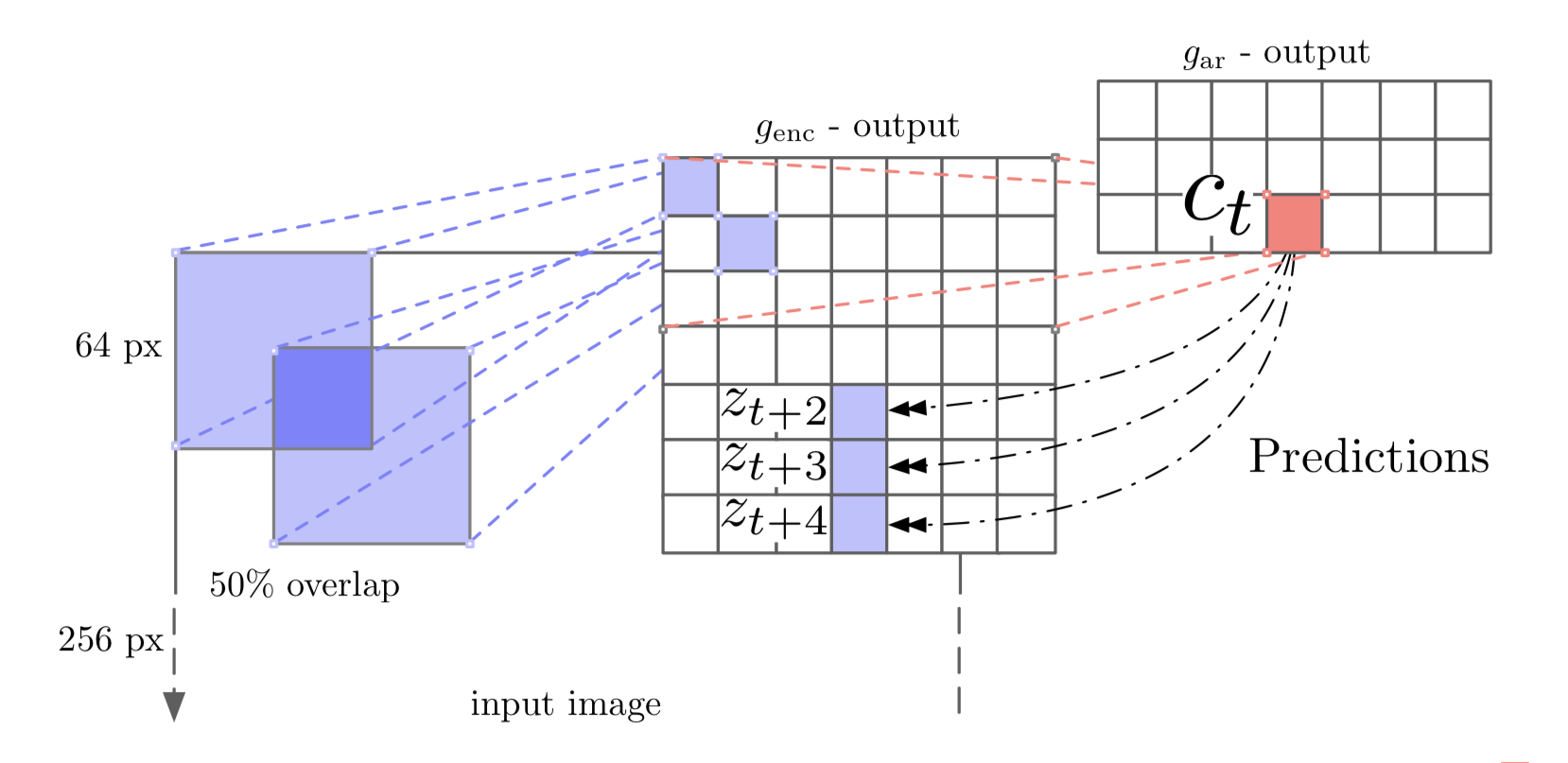
When using CPC on images (Henaff, et al. 2019), the predictor network should only access a masked feature set to avoid a trivial prediction. Precisely:
- Each input image is divided into a set of overlapped patches and each patch is encoded by a resnet encoder, resulting in compressed feature vector $z_{i,j}$.
- A masked conv net makes prediction with a mask such that the receptive field of a given output neuron can only see things above it in the image. Otherwise, the prediction problem would be trivial. The prediction can be made in both directions (top-down and bottom-up).
- The prediction is made for $z_{i+k, j}$ from context $c_{i,j}$: $\hat{z}_{i+k, j} = W_k c_{i,j}$.
A contrastive loss quantifies this prediction with a goal to correctly identify the target among a set of negative representation $\{z_l\}$ sampled from other patches in the same image and other images in the same batch:
For more content on contrastive learning, check out the post on “Contrastive Representation Learning”.
Video-Based
A video contains a sequence of semantically related frames. Nearby frames are close in time and more correlated than frames further away. The order of frames describes certain rules of reasonings and physical logics; such as that object motion should be smooth and gravity is pointing down.
A common workflow is to train a model on one or multiple pretext tasks with unlabelled videos and then feed one intermediate feature layer of this model to fine-tune a simple model on downstream tasks of action classification, segmentation or object tracking.
Tracking
The movement of an object is traced by a sequence of video frames. The difference between how the same object is captured on the screen in close frames is usually not big, commonly triggered by small motion of the object or the camera. Therefore any visual representation learned for the same object across close frames should be close in the latent feature space. Motivated by this idea, Wang & Gupta, 2015 proposed a way of unsupervised learning of visual representation by tracking moving objects in videos.
Precisely patches with motion are tracked over a small time window (e.g. 30 frames). The first patch $\mathbf{x}$ and the last patch $\mathbf{x}^+$ are selected and used as training data points. If we train the model directly to minimize the difference between feature vectors of two patches, the model may only learn to map everything to the same value. To avoid such a trivial solution, same as above, a random third patch $\mathbf{x}^-$ is added. The model learns the representation by enforcing the distance between two tracked patches to be closer than the distance between the first patch and a random one in the feature space, $D(\mathbf{x}, \mathbf{x}^-)) > D(\mathbf{x}, \mathbf{x}^+)$, where $D(.)$ is the cosine distance,
The loss function is:
where $M$ is a scalar constant controlling for the minimum gap between two distances; $M=0.5$ in the paper. The loss enforces $D(\mathbf{x}, \mathbf{x}^-) >= D(\mathbf{x}, \mathbf{x}^+) + M$ at the optimal case.
This form of loss function is also known as triplet loss in the face recognition task, in which the dataset contains images of multiple people from multiple camera angles. Let $\mathbf{x}^a$ be an anchor image of a specific person, $\mathbf{x}^p$ be a positive image of this same person from a different angle and $\mathbf{x}^n$ be a negative image of a different person. In the embedding space, $\mathbf{x}^a$ should be closer to $\mathbf{x}^p$ than $\mathbf{x}^n$:
A slightly different form of the triplet loss, named n-pair loss is also commonly used for learning observation embedding in robotics tasks. See a later section for more related content.
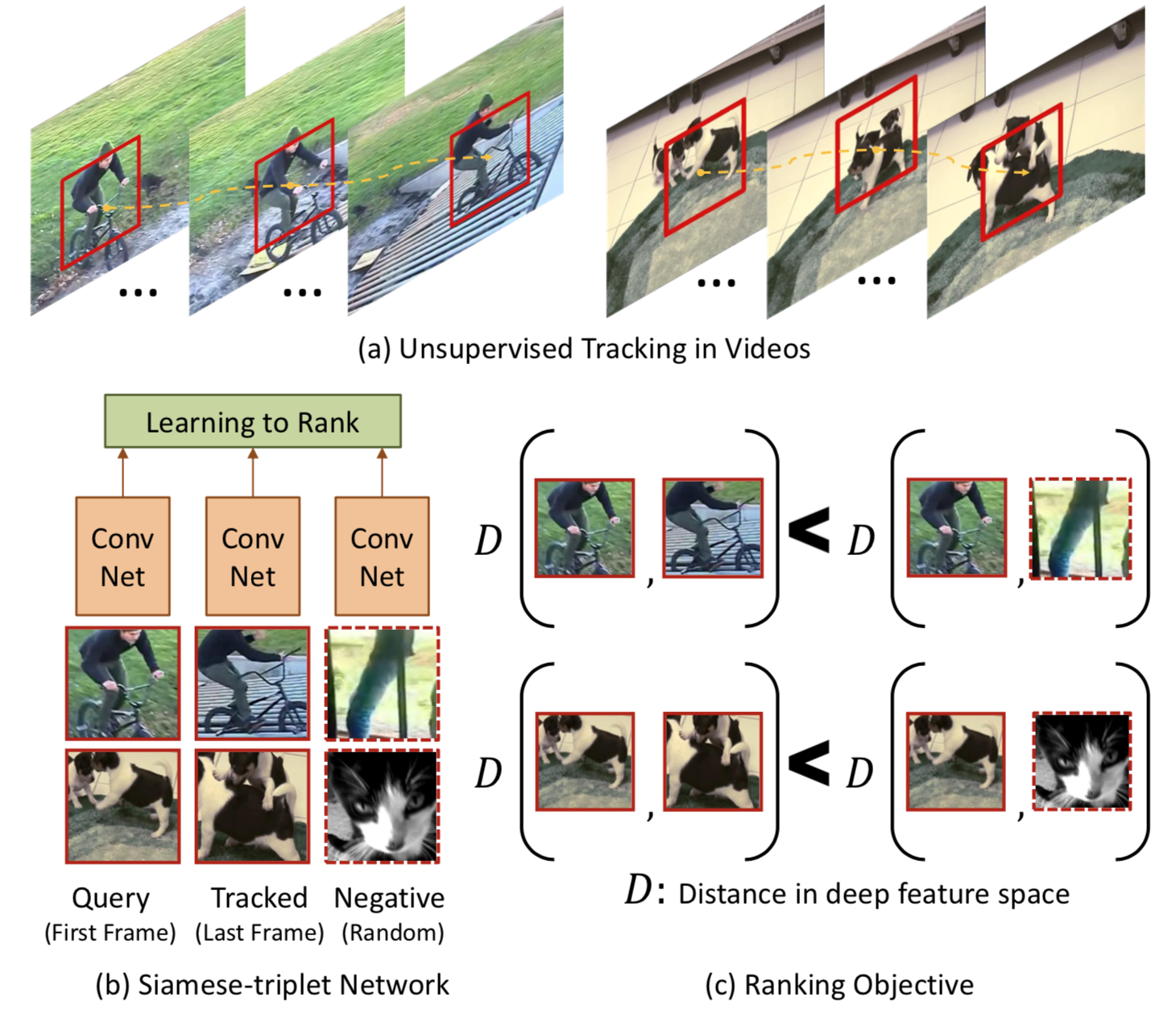
Relevant patches are tracked and extracted through a two-step unsupervised optical flow approach:
- Obtain SURF interest points and use IDT to obtain motion of each SURF point.
- Given the trajectories of SURF interest points, classify these points as moving if the flow magnitude is more than 0.5 pixels.
During training, given a pair of correlated patches $\mathbf{x}$ and $\mathbf{x}^+$, $K$ random patches $\{\mathbf{x}^-\}$ are sampled in this same batch to form $K$ training triplets. After a couple of epochs, hard negative mining is applied to make the training harder and more efficient, that is, to search for random patches that maximize the loss and use them to do gradient updates.
Frame Sequence
Video frames are naturally positioned in chronological order. Researchers have proposed several self-supervised tasks, motivated by the expectation that good representation should learn the correct sequence of frames.
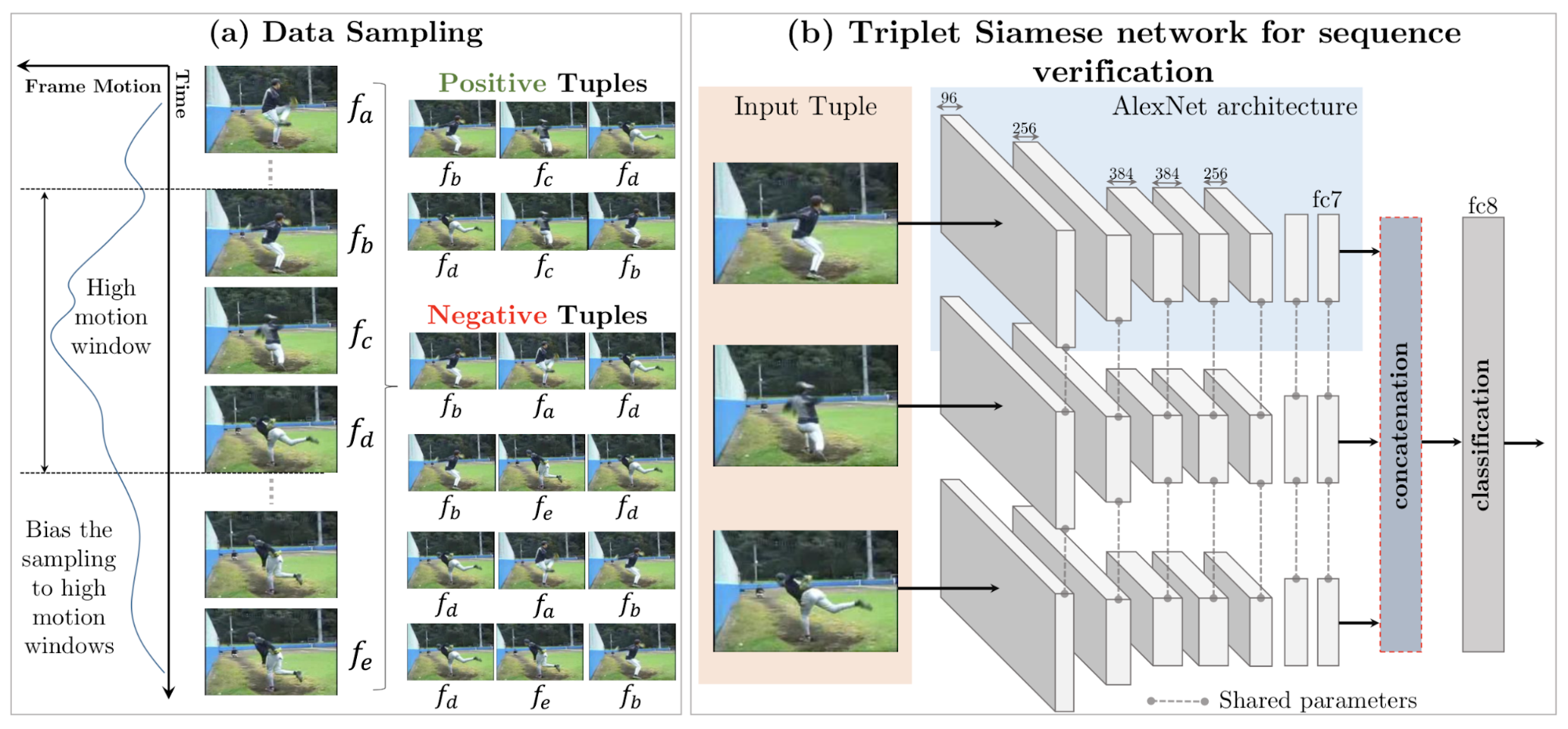
One idea is to validate frame order (Misra, et al 2016). The pretext task is to determine whether a sequence of frames from a video is placed in the correct temporal order (“temporal valid”). The model needs to track and reason about small motion of an object across frames to complete such a task.
The training frames are sampled from high-motion windows. Every time 5 frames are sampled $(f_a, f_b, f_c, f_d, f_e)$ and the timestamps are in order $a < b < c < d < e$. Out of 5 frames, one positive tuple $(f_b, f_c, f_d)$ and two negative tuples, $(f_b, f_a, f_d)$ and $(f_b, f_e, f_d)$ are created. The parameter $\tau_\max = \vert b-d \vert$ controls the difficulty of positive training instances (i.e. higher → harder) and the parameter $\tau_\min = \min(\vert a-b \vert, \vert d-e \vert)$ controls the difficulty of negatives (i.e. lower → harder).
The pretext task of video frame order validation is shown to improve the performance on the downstream task of action recognition when used as a pretraining step.
The task in O3N (Odd-One-Out Network; Fernando et al. 2017) is based on video frame sequence validation too. One step further from above, the task is to pick the incorrect sequence from multiple video clips.
Given $N+1$ input video clips, one of them has frames shuffled, thus in the wrong order, and the rest $N$ of them remain in the correct temporal order. O3N learns to predict the location of the odd video clip. In their experiments, there are 6 input clips and each contain 6 frames.
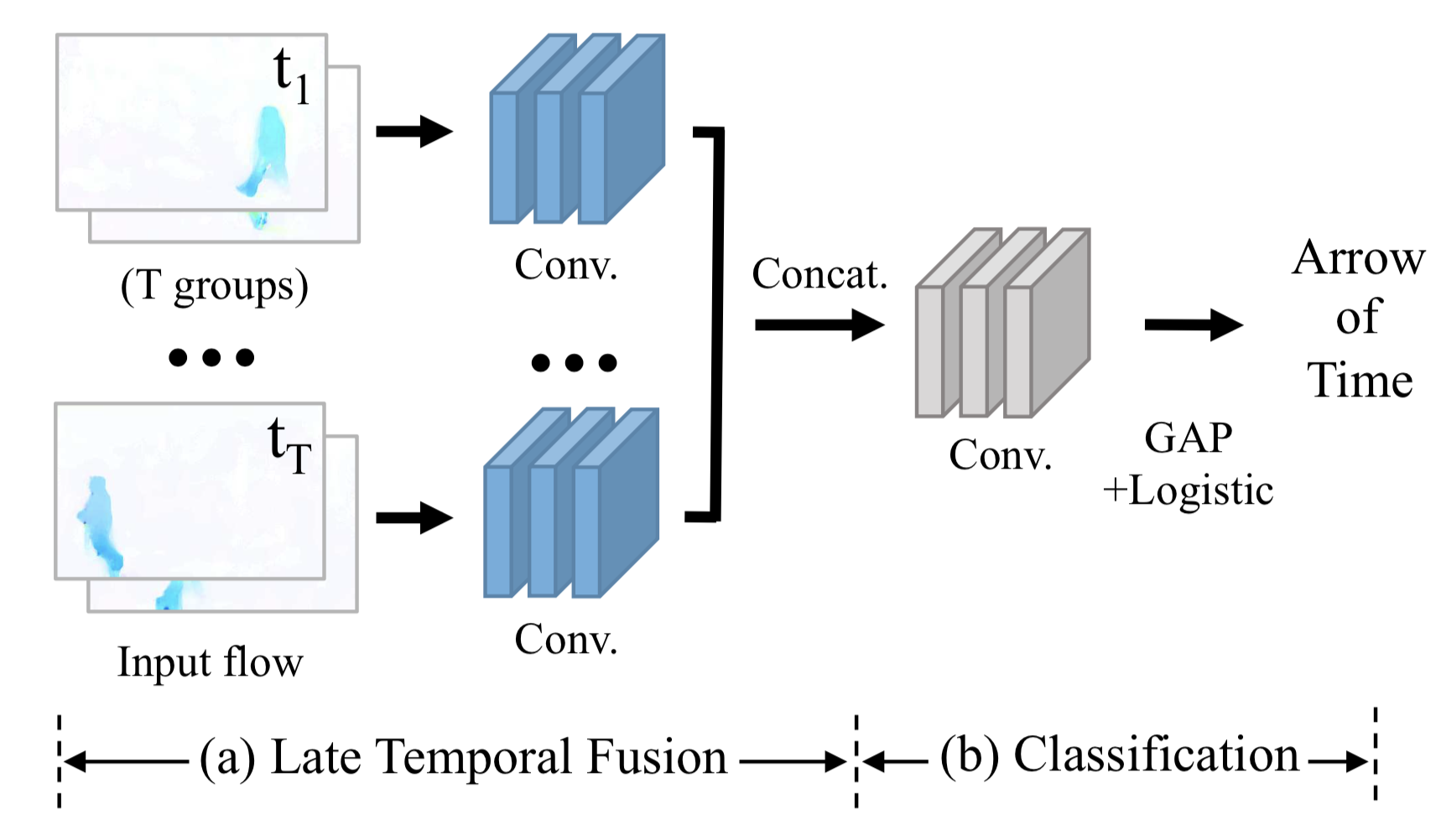
The arrow of time in a video contains very informative messages, on both low-level physics (e.g. gravity pulls objects down to the ground; smoke rises up; water flows downward.) and high-level event reasoning (e.g. fish swim forward; you can break an egg but cannot revert it.). Thus another idea is inspired by this to learn latent representation by predicting the arrow of time (AoT) — whether video playing forwards or backwards (Wei et al., 2018).
A classifier should capture both low-level physics and high-level semantics in order to predict the arrow of time. The proposed T-CAM (Temporal Class-Activation-Map) network accepts $T$ groups, each containing a number of frames of optical flow. The conv layer outputs from each group are concatenated and fed into binary logistic regression for predicting the arrow of time.
Interestingly, there exist a couple of artificial cues in the dataset. If not handled properly, they could lead to a trivial classifier without relying on the actual video content:
- Due to the video compression, the black framing might not be completely black but instead may contain certain information on the chronological order. Hence black framing should be removed in the experiments.
- Large camera motion, like vertical translation or zoom-in/out, also provides strong signals for the arrow of time but independent of content. The processing stage should stabilize the camera motion.
The AoT pretext task is shown to improve the performance on action classification downstream task when used as a pretraining step. Note that fine-tuning is still needed.
Video Colorization
Vondrick et al. (2018) proposed video colorization as a self-supervised learning problem, resulting in a rich representation that can be used for video segmentation and unlabelled visual region tracking, without extra fine-tuning.
Unlike the image-based colorization, here the task is to copy colors from a normal reference frame in color to another target frame in grayscale by leveraging the natural temporal coherency of colors across video frames (thus these two frames shouldn’t be too far apart in time). In order to copy colors consistently, the model is designed to learn to keep track of correlated pixels in different frames.
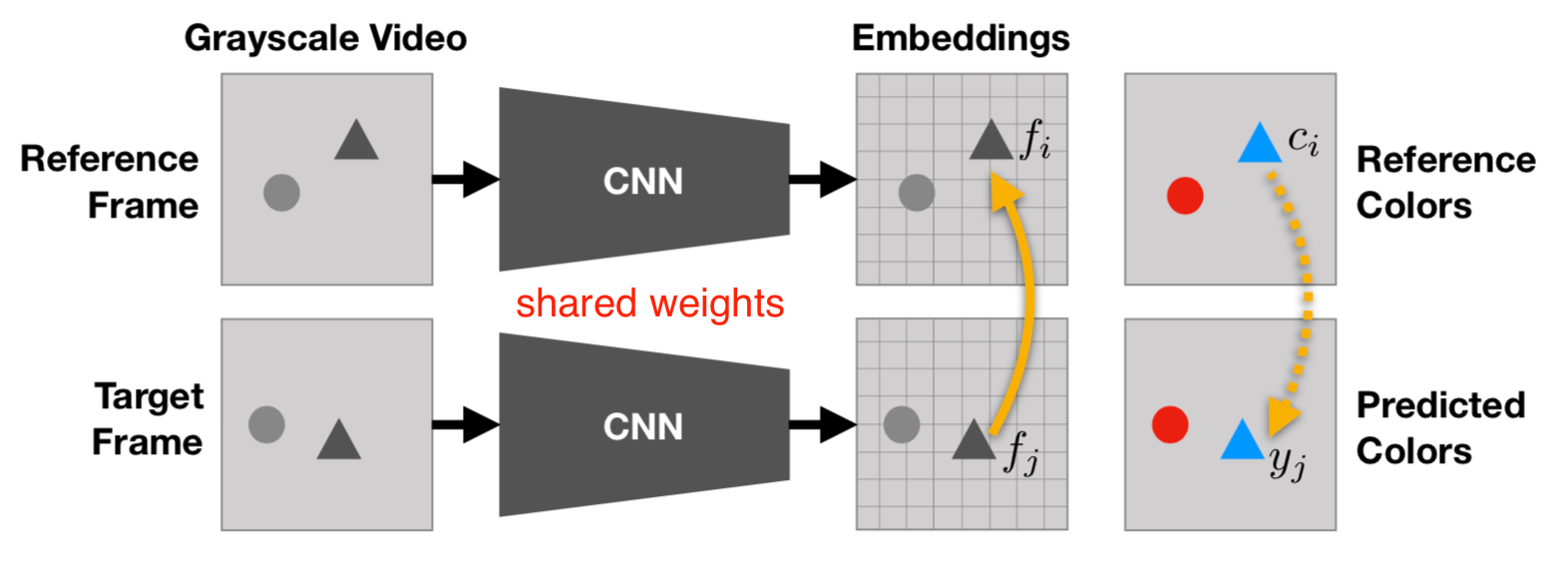
The idea is quite simple and smart. Let $c_i$ be the true color of the $i-th$ pixel in the reference frame and $c_j$ be the color of $j$-th pixel in the target frame. The predicted color of $j$-th color in the target $\hat{c}_j$ is a weighted sum of colors of all the pixels in reference, where the weighting term measures the similarity:
where $f$ are learned embeddings for corresponding pixels; $i’$ indexes all the pixels in the reference frame. The weighting term implements an attention-based pointing mechanism, similar to matching network and pointer network. As the full similarity matrix could be really large, both frames are downsampled. The categorical cross-entropy loss between $c_j$ and $\hat{c}_j$ is used with quantized colors, just like in Zhang et al. 2016.
Based on how the reference frame are marked, the model can be used to complete several color-based downstream tasks such as tracking segmentation or human pose in time. No fine-tuning is needed. See 
A couple common observations:
- Combining multiple pretext tasks improves performance;
- Deeper networks improve the quality of representation;
- Supervised learning baselines still beat all of them by far.
Control-Based
When running a RL policy in the real world, such as controlling a physical robot on visual inputs, it is non-trivial to properly track states, obtain reward signals or determine whether a goal is achieved for real. The visual data has a lot of noise that is irrelevant to the true state and thus the equivalence of states cannot be inferred from pixel-level comparison. Self-supervised representation learning has shown great potential in learning useful state embedding that can be used directly as input to a control policy.
All the cases discussed in this section are in robotic learning, mainly for state representation from multiple camera views and goal representation.
Multi-View Metric Learning
The concept of metric learning has been mentioned multiple times in the previous sections. A common setting is: Given a triple of samples, (anchor $s_a$, positive sample $s_p$, negative sample $s_n$), the learned representation embedding $\phi(s)$ fulfills that $s_a$ stays close to $s_p$ but far away from $s_n$ in the latent space.
Grasp2Vec (Jang & Devin et al., 2018) aims to learn an object-centric vision representation in the robot grasping task from free, unlabelled grasping activities. By object-centric, it means that, irrespective of how the environment or the robot looks like, if two images contain similar items, they should be mapped to similar representation; otherwise the embeddings should be far apart.
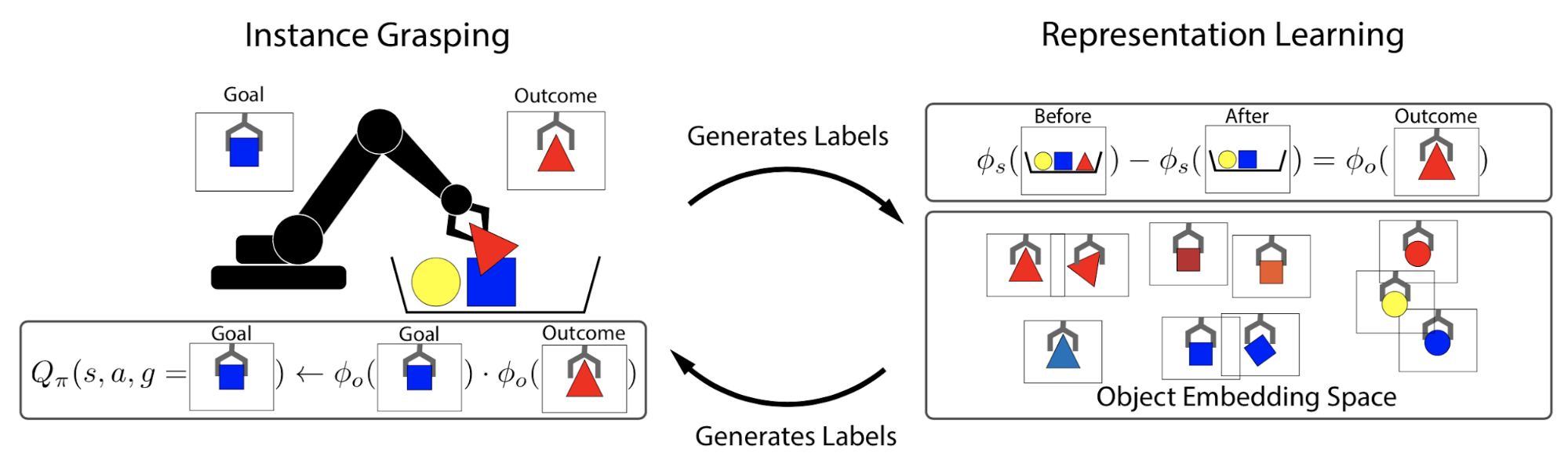
The grasping system can tell whether it moves an object but cannot tell which object it is. Cameras are set up to take images of the entire scene and the grasped object. During early training, the grasp robot is executed to grasp any object $o$ at random, producing a triple of images, $(s_\text{pre}, s_\text{post}, o)$:
- $o$ is an image of the grasped object held up to the camera;
- $s_\text{pre}$ is an image of the scene before grasping, with the object $o$ in the tray;
- $s_\text{post}$ is an image of the same scene after grasping, without the object $o$ in the tray.
To learn object-centric representation, we expect the difference between embeddings of $s_\text{pre}$ and $s_\text{post}$ to capture the removed object $o$. The idea is quite interesting and similar to relationships that have been observed in word embedding, e.g. distance(“king”, “queen”) ≈ distance(“man”, “woman”).
Let $\phi_s$ and $\phi_o$ be the embedding functions for the scene and the object respectively. The model learns the representation by minimizing the distance between $\phi_s(s_\text{pre}) - \phi_s(s_\text{post})$ and $\phi_o(o)$ using n-pair loss:
where $B$ refers to a batch of (anchor, positive) sample pairs.
When framing representation learning as metric learning, n-pair loss is a common choice. Rather than processing explicit a triple of (anchor, positive, negative) samples, the n-pairs loss treats all other positive instances in one mini-batch across pairs as negatives.
The embedding function $\phi_o$ works great for presenting a goal $g$ with an image. The reward function that quantifies how close the actually grasped object $o$ is close to the goal is defined as $r = \phi_o(g) \cdot \phi_o(o)$. Note that computing rewards only relies on the learned latent space and doesn’t involve ground truth positions, so it can be used for training on real robots.

Other than the embedding-similarity-based reward function, there are a few other tricks for training the RL policy in the grasp2vec framework:
- Posthoc labeling: Augment the dataset by labeling a randomly grasped object as a correct goal, like HER (Hindsight Experience Replay; Andrychowicz, et al., 2017).
- Auxiliary goal augmentation: Augment the replay buffer even further by relabeling transitions with unachieved goals; precisely, in each iteration, two goals are sampled $(g, g’)$ and both are used to add new transitions into replay buffer.
TCN (Time-Contrastive Networks; Sermanet, et al. 2018) learn from multi-camera view videos with the intuition that different viewpoints at the same timestep of the same scene should share the same embedding (like in FaceNet) while embedding should vary in time, even of the same camera viewpoint. Therefore embedding captures the semantic meaning of the underlying state rather than visual similarity. The TCN embedding is trained with triplet loss.
The training data is collected by taking videos of the same scene simultaneously but from different angles. All the videos are unlabelled.
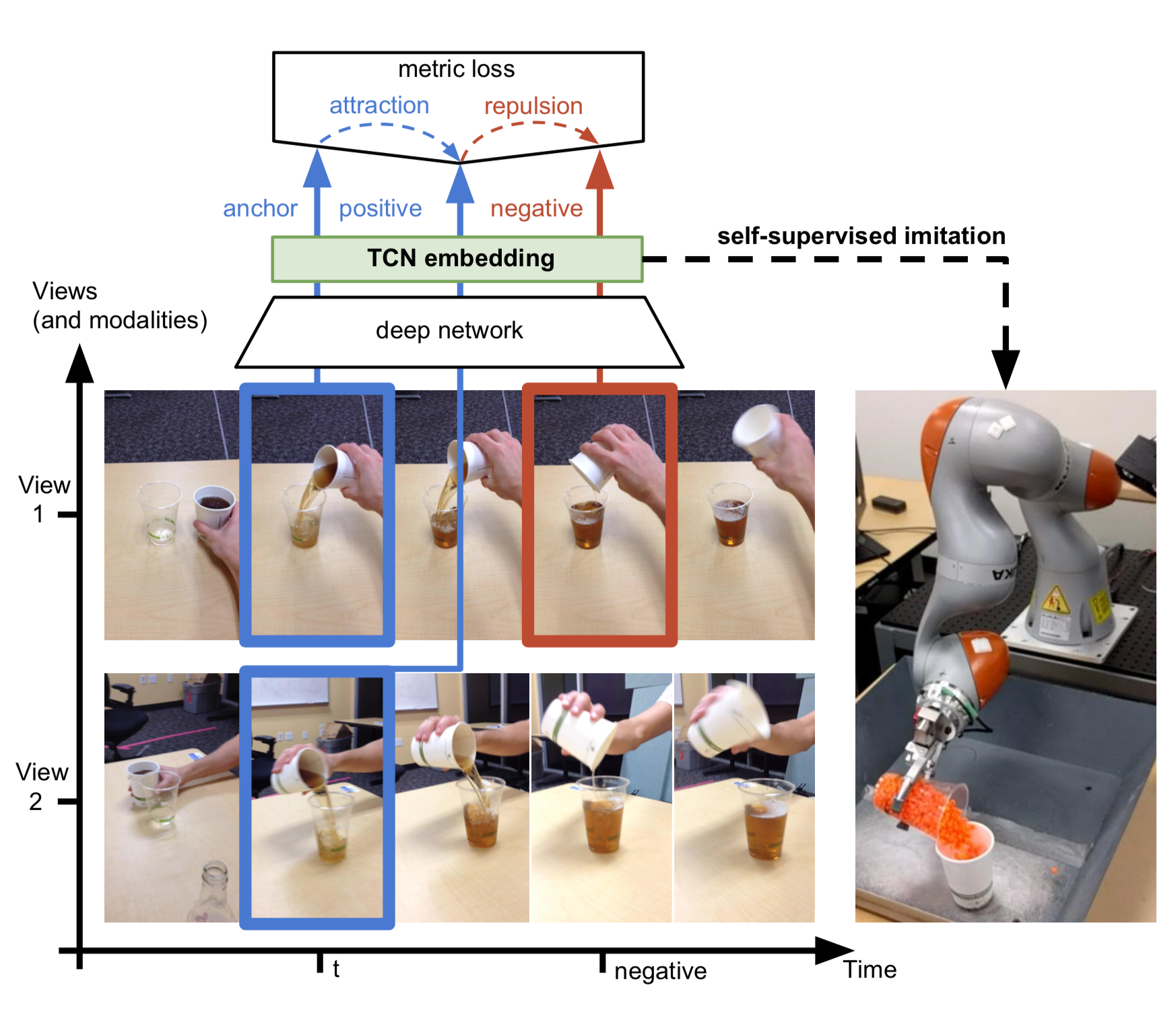
TCN embedding extracts visual features that are invariant to camera configurations. It can be used to construct a reward function for imitation learning based on the euclidean distance between the demo video and the observations in the latent space.
A further improvement over TCN is to learn embedding over multiple frames jointly rather than a single frame, resulting in mfTCN (Multi-frame Time-Contrastive Networks; Dwibedi et al., 2019). Given a set of videos from several synchronized camera viewpoints, $v_1, v_2, \dots, v_k$, the frame at time $t$ and the previous $n-1$ frames selected with stride $s$ in each video are aggregated and mapped into one embedding vector, resulting in a lookback window of size $(n−1) \times s + 1$. Each frame first goes through a CNN to extract low-level features and then we use 3D temporal convolutions to aggregate frames in time. The model is trained with n-pairs loss.
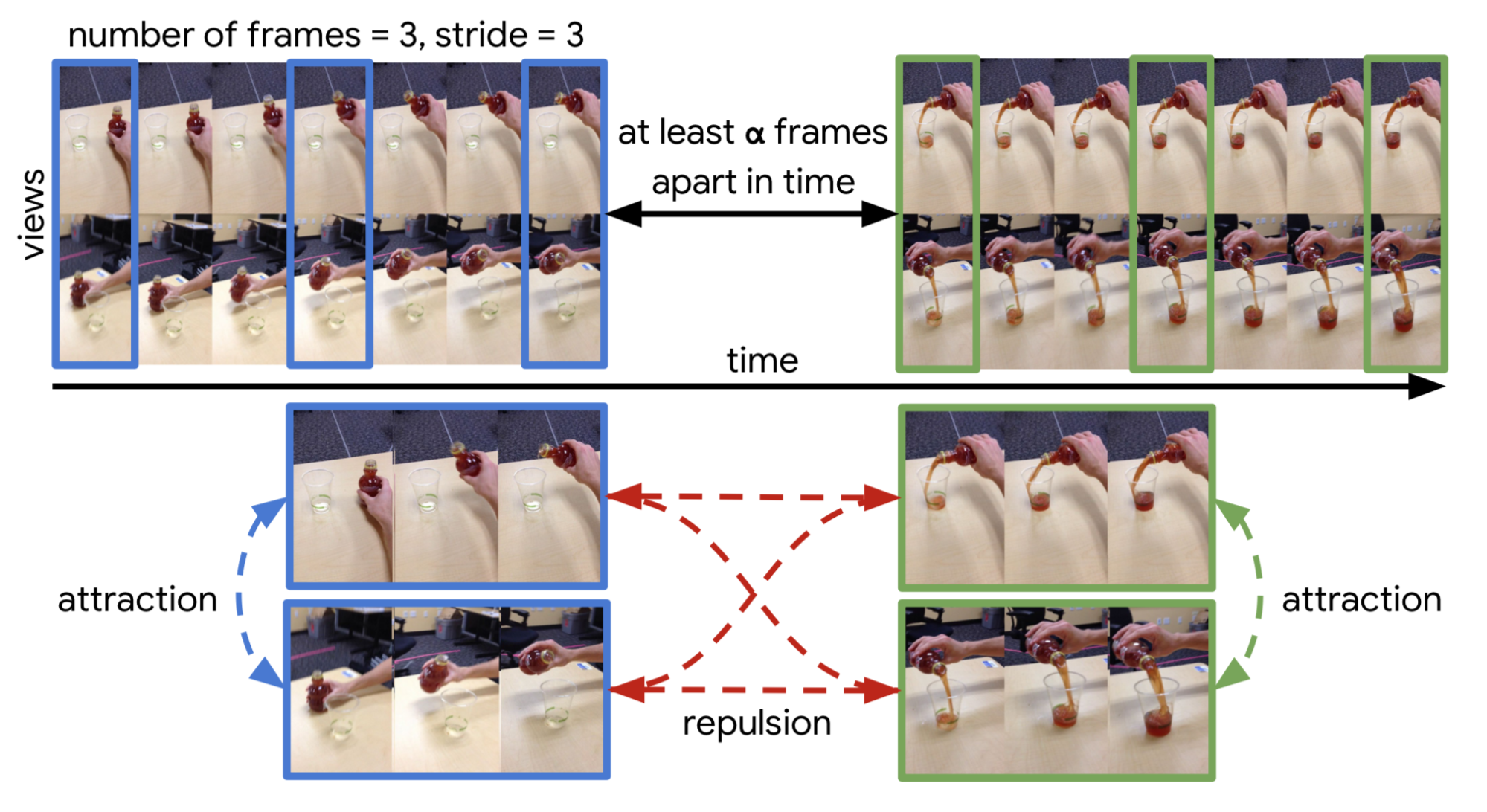
The training data is sampled as follows:
- First we construct two pairs of video clips. Each pair contains two clips from different camera views but with synchronized timesteps. These two sets of videos should be far apart in time.
- Sample a fixed number of frames from each video clip in the same pair simultaneously with the same stride.
- Frames with the same timesteps are trained as positive samples in the n-pair loss, while frames across pairs are negative samples.
mfTCN embedding can capture the position and velocity of objects in the scene (e.g. in cartpole) and can also be used as inputs for policy.
Autonomous Goal Generation
RIG (Reinforcement learning with Imagined Goals; Nair et al., 2018) described a way to train a goal-conditioned policy with unsupervised representation learning. A policy learns from self-supervised practice by first imagining “fake” goals and then trying to achieve them.
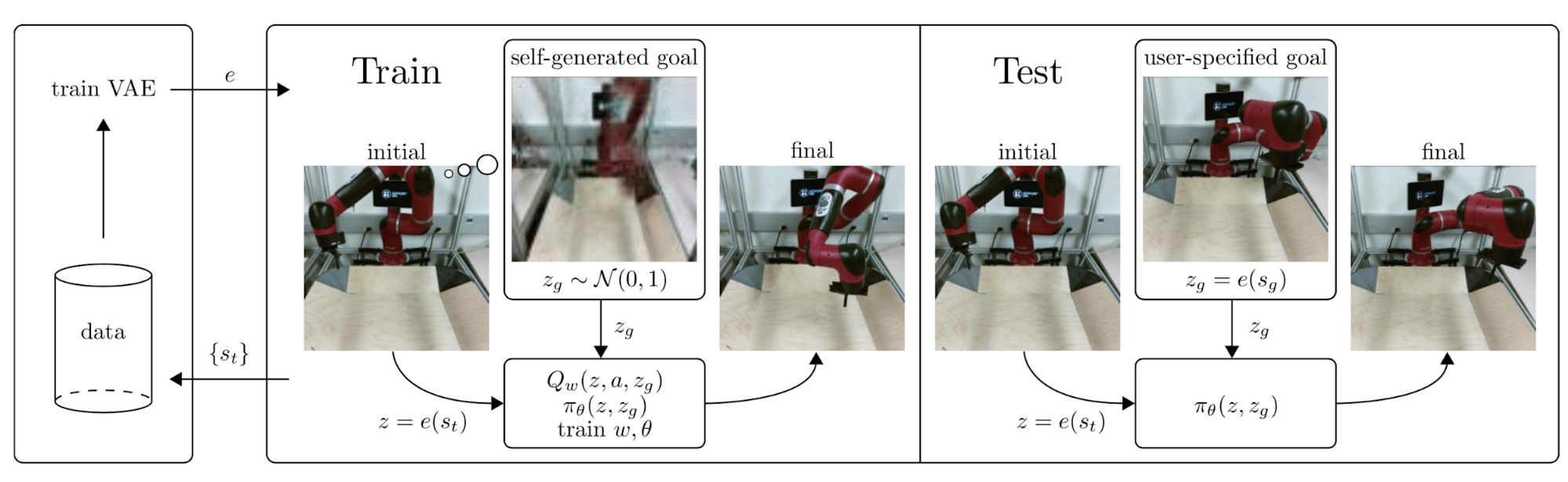
The task is to control a robot arm to push a small puck on a table to a desired position. The desired position, or the goal, is present in an image. During training, it learns latent embedding of both state $s$ and goal $g$ through $\beta$-VAE encoder and the control policy operates entirely in the latent space.
Let’s say a $\beta$-VAE has an encoder $q_\phi$ mapping input states to latent variable $z$ which is modeled by a Gaussian distribution and a decoder $p_\psi$ mapping $z$ back to the states. The state encoder in RIG is set to be the mean of $\beta$-VAE encoder.
The reward is the Euclidean distance between state and goal embedding vectors: $r(s, g) = -|e(s) - e(g)|$. Similar to grasp2vec, RIG applies data augmentation as well by latent goal relabeling: precisely half of the goals are generated from the prior at random and the other half are selected using HER. Also same as grasp2vec, rewards do not depend on any ground truth states but only the learned state encoding, so it can be used for training on real robots.

The problem with RIG is a lack of object variations in the imagined goal pictures. If $\beta$-VAE is only trained with a black puck, it would not be able to create a goal with other objects like blocks of different shapes and colors. A follow-up improvement replaces $\beta$-VAE with a CC-VAE (Context-Conditioned VAE; Nair, et al., 2019), inspired by CVAE (Conditional VAE; Sohn, Lee & Yan, 2015), for goal generation.
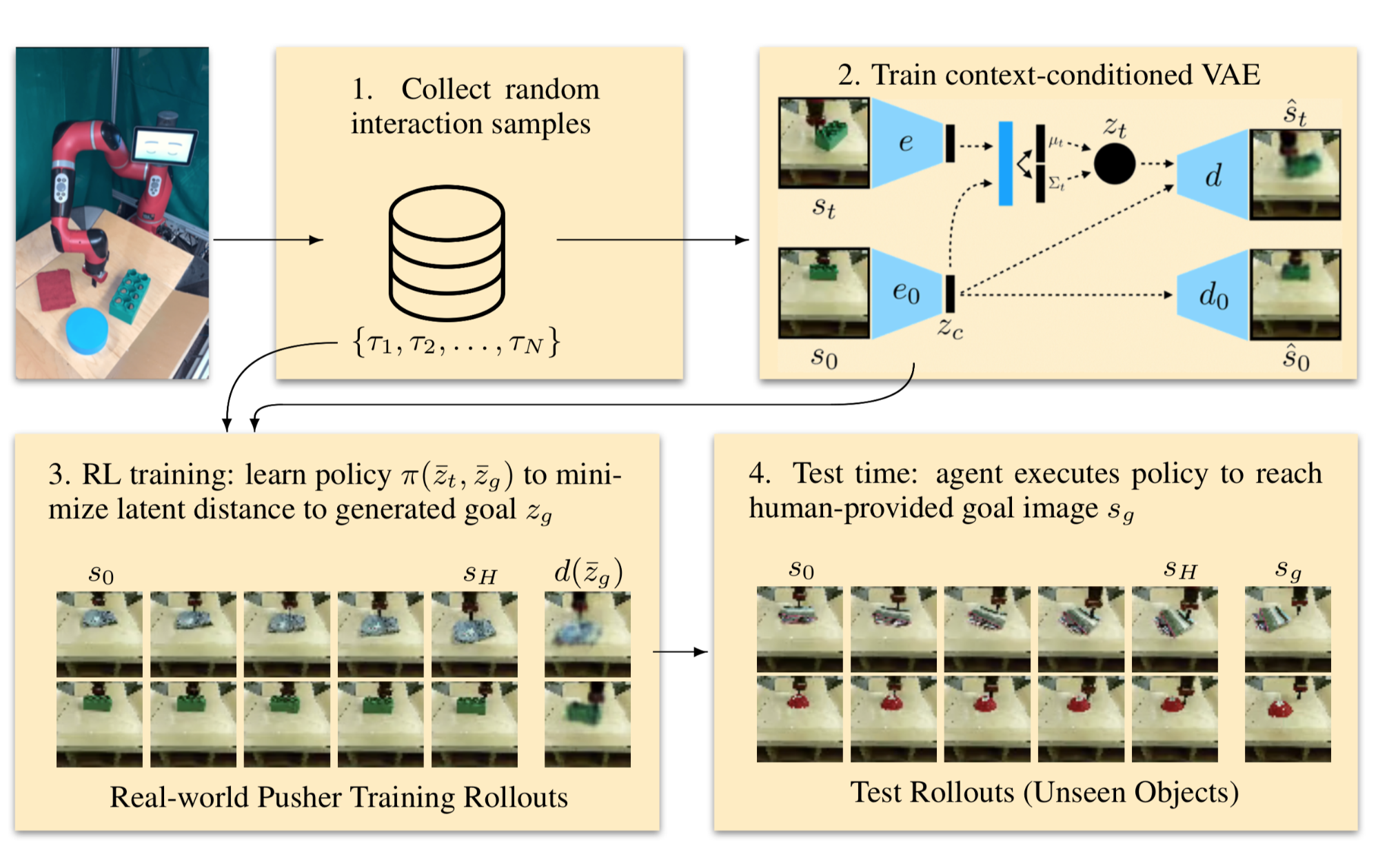
A CVAE conditions on a context variable $c$. It trains an encoder $q_\phi(z \vert s, c)$ and a decoder $p_\psi (s \vert z, c)$ and note that both have access to $c$. The CVAE loss penalizes information passing from the input state $s$ through an information bottleneck but allows for unrestricted information flow from $c$ to both encoder and decoder.
To create plausible goals, CC-VAE conditions on a starting state $s_0$ so that the generated goal presents a consistent type of object as in $s_0$. This goal consistency is necessary; e.g. if the current scene contains a red puck but the goal has a blue block, it would confuse the policy.
Other than the state encoder $e(s) \triangleq \mu_\phi(s)$, CC-VAE trains a second convolutional encoder $e_0(.)$ to translate the starting state $s_0$ into a compact context representation $c = e_0(s_0)$. Two encoders, $e(.)$ and $e_0(.)$, are intentionally different without shared weights, as they are expected to encode different factors of image variation. In addition to the loss function of CVAE, CC-VAE adds an extra term to learn to reconstruct $c$ back to $s_0$, $\hat{s}_0 = d_0(c)$.

Bisimulation
Task-agnostic representation (e.g. a model that intends to represent all the dynamics in the system) may distract the RL algorithms as irrelevant information is also presented. For example, if we just train an auto-encoder to reconstruct the input image, there is no guarantee that the entire learned representation will be useful for RL. Therefore, we need to move away from reconstruction-based representation learning if we only want to learn information relevant to control, as irrelevant details are still important for reconstruction.
Representation learning for control based on bisimulation does not depend on reconstruction, but aims to group states based on their behavioral similarity in MDP.
Bisimulation (Givan et al. 2003) refers to an equivalence relation between two states with similar long-term behavior. Bisimulation metrics quantify such relation so that we can aggregate states to compress a high-dimensional state space into a smaller one for more efficient computation. The bisimulation distance between two states corresponds to how behaviorally different these two states are.
Given a MDP $\mathcal{M} = \langle \mathcal{S}, \mathcal{A}, \mathcal{P}, \mathcal{R}, \gamma \rangle$ and a bisimulation relation $B$, two states that are equal under relation $B$ (i.e. $s_i B s_j$) should have the same immediate reward for all actions and the same transition probabilities over the next bisimilar states:
where $\mathcal{S}_B$ is a partition of the state space under the relation $B$.
Note that $=$ is always a bisimulation relation. The most interesting one is the maximal bisimulation relation $\sim$, which defines a partition $\mathcal{S}_\sim$ with fewest groups of states.
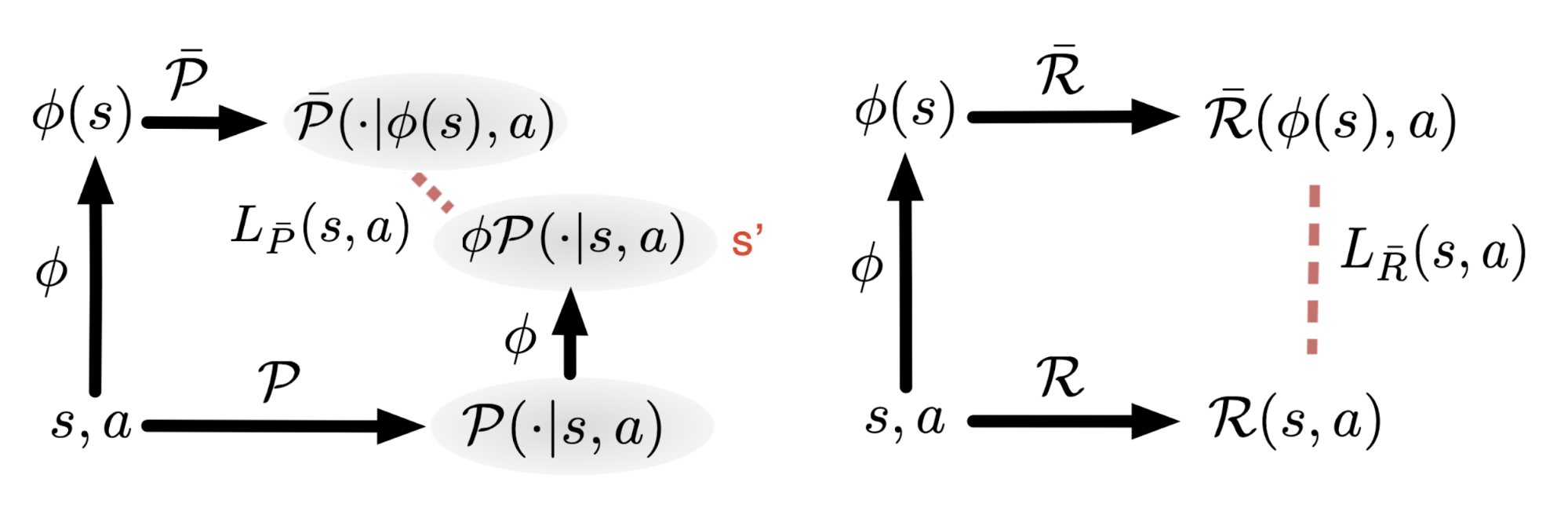
With a goal similar to bisimulation metric, DeepMDP (Gelada, et al. 2019) simplifies high-dimensional observations in RL tasks and learns a latent space model via minimizing two losses:
- prediction of rewards and
- prediction of the distribution over next latent states.
where $\phi(s)$ is the embedding of state $s$; symbols with bar are functions (reward function $R$ and transition function $P$) in the same MDP but running in the latent low-dimensional observation space. Here the embedding representation $\phi$ can be connected to bisimulation metrics, as the bisimulation distance is proved to be upper-bounded by the L2 distance in the latent space.
The function $D$ quantifies the distance between two probability distributions and should be chosen carefully. DeepMDP focuses on Wasserstein-1 metric (also known as “earth-mover distance”). The Wasserstein-1 distance between distributions $P$ and $Q$ on a metric space $(M, d)$ (i.e., $d: M \times M \to \mathbb{R}$) is:
where $\Pi(P, Q)$ is the set of all couplings of $P$ and $Q$. $d(x, y)$ defines the cost of moving a particle from point $x$ to point $y$.
The Wasserstein metric has a dual form according to the Monge-Kantorovich duality:
where $\mathcal{F}_d$ is the set of 1-Lipschitz functions under the metric $d$ - $\mathcal{F}_d = \{ f: \vert f(x) - f(y) \vert \leq d(x, y) \}$.
DeepMDP generalizes the model to the Norm Maximum Mean Discrepancy (Norm-MMD) metrics to improve the tightness of the bounds of its deep value function and, at the same time, to save computation (Wasserstein is expensive computationally). In their experiments, they found the model architecture of the transition prediction model can have a big impact on the performance. Adding these DeepMDP losses as auxiliary losses when training model-free RL agents leads to good improvement on most of the Atari games.
Deep Bisimulatioin for Control (short for DBC; Zhang et al. 2020) learns the latent representation of observations that are good for control in RL tasks, without domain knowledge or pixel-level reconstruction.
Similar to DeepMDP, DBC models the dynamics by learning a reward model and a transition model. Both models operate in the latent space, $\phi(s)$. The optimization of embedding $\phi$ depends on one important conclusion from Ferns, et al. 2004 (Theorem 4.5) and Ferns, et al 2011 (Theorem 2.6):
Given $c \in (0, 1)$ a discounting factor, $\pi$ a policy that is being improved continuously, and $M$ the space of bounded pseudometric on the state space $\mathcal{S}$, we can define $\mathcal{F}: M \mapsto M$:
$$ \mathcal{F}(d; \pi)(s_i, s_j) = (1-c) \vert \mathcal{R}_{s_i}^\pi - \mathcal{R}_{s_j}^\pi \vert + c W_d (\mathcal{P}_{s_i}^\pi, \mathcal{P}_{s_j}^\pi) $$Then, $\mathcal{F}$ has a unique fixed point $\tilde{d}$ which is a $\pi^*$-bisimulation metric and $\tilde{d}(s_i, s_j) = 0 \iff s_i \sim s_j$.
[The proof is not trivial. I may or may not add it in the future _(:3」∠)_ …]
Given batches of observations pairs, the training loss for $\phi$, $J(\phi)$, minimizes the mean square error between the on-policy bisimulation metric and Euclidean distance in the latent space:
where $\bar{\phi}(s)$ denotes $\phi(s)$ with stop gradient and $\bar{\pi}$ is the mean policy output. The learned reward model $\hat{\mathcal{R}}$ is deterministic and the learned forward dynamics model $\hat{\mathcal{P}}$ outputs a Gaussian distribution.
DBC is based on SAC but operates on the latent space:

Cited as:
@article{weng2019selfsup,
title = "Self-Supervised Representation Learning",
author = "Weng, Lilian",
journal = "lilianweng.github.io",
year = "2019",
url = "https://lilianweng.github.io/posts/2019-11-10-self-supervised/"
}
References
[1] Alexey Dosovitskiy, et al. “Discriminative unsupervised feature learning with exemplar convolutional neural networks.” IEEE transactions on pattern analysis and machine intelligence 38.9 (2015): 1734-1747.
[2] Spyros Gidaris, Praveer Singh & Nikos Komodakis. “Unsupervised Representation Learning by Predicting Image Rotations” ICLR 2018.
[3] Carl Doersch, Abhinav Gupta, and Alexei A. Efros. “Unsupervised visual representation learning by context prediction.” ICCV. 2015.
[4] Mehdi Noroozi & Paolo Favaro. “Unsupervised learning of visual representations by solving jigsaw puzzles.” ECCV, 2016.
[5] Mehdi Noroozi, Hamed Pirsiavash, and Paolo Favaro. “Representation learning by learning to count.” ICCV. 2017.
[6] Richard Zhang, Phillip Isola & Alexei A. Efros. “Colorful image colorization.” ECCV, 2016.
[7] Pascal Vincent, et al. “Extracting and composing robust features with denoising autoencoders.” ICML, 2008.
[8] Jeff Donahue, Philipp Krähenbühl, and Trevor Darrell. “Adversarial feature learning.” ICLR 2017.
[9] Deepak Pathak, et al. “Context encoders: Feature learning by inpainting.” CVPR. 2016.
[10] Richard Zhang, Phillip Isola, and Alexei A. Efros. “Split-brain autoencoders: Unsupervised learning by cross-channel prediction.” CVPR. 2017.
[11] Xiaolong Wang & Abhinav Gupta. “Unsupervised Learning of Visual Representations using Videos.” ICCV. 2015.
[12] Carl Vondrick, et al. “Tracking Emerges by Colorizing Videos” ECCV. 2018.
[13] Ishan Misra, C. Lawrence Zitnick, and Martial Hebert. “Shuffle and learn: unsupervised learning using temporal order verification.” ECCV. 2016.
[14] Basura Fernando, et al. “Self-Supervised Video Representation Learning With Odd-One-Out Networks” CVPR. 2017.
[15] Donglai Wei, et al. “Learning and Using the Arrow of Time” CVPR. 2018.
[16] Florian Schroff, Dmitry Kalenichenko and James Philbin. “FaceNet: A Unified Embedding for Face Recognition and Clustering” CVPR. 2015.
[17] Pierre Sermanet, et al. “Time-Contrastive Networks: Self-Supervised Learning from Video” CVPR. 2018.
[18] Debidatta Dwibedi, et al. “Learning actionable representations from visual observations.” IROS. 2018.
[19] Eric Jang & Coline Devin, et al. “Grasp2Vec: Learning Object Representations from Self-Supervised Grasping” CoRL. 2018.
[20] Ashvin Nair, et al. “Visual reinforcement learning with imagined goals” NeuriPS. 2018.
[21] Ashvin Nair, et al. “Contextual imagined goals for self-supervised robotic learning” CoRL. 2019.
[22] Aaron van den Oord, Yazhe Li & Oriol Vinyals. “Representation Learning with Contrastive Predictive Coding” arXiv preprint arXiv:1807.03748, 2018.
[23] Olivier J. Henaff, et al. “Data-Efficient Image Recognition with Contrastive Predictive Coding” arXiv preprint arXiv:1905.09272, 2019.
[24] Kaiming He, et al. “Momentum Contrast for Unsupervised Visual Representation Learning.” CVPR 2020.
[25] Zhirong Wu, et al. “Unsupervised Feature Learning via Non-Parametric Instance-level Discrimination.” CVPR 2018.
[26] Ting Chen, et al. “A Simple Framework for Contrastive Learning of Visual Representations.” arXiv preprint arXiv:2002.05709, 2020.
[27] Aravind Srinivas, Michael Laskin & Pieter Abbeel “CURL: Contrastive Unsupervised Representations for Reinforcement Learning.” arXiv preprint arXiv:2004.04136, 2020.
[28] Carles Gelada, et al. “DeepMDP: Learning Continuous Latent Space Models for Representation Learning” ICML 2019.
[29] Amy Zhang, et al. “Learning Invariant Representations for Reinforcement Learning without Reconstruction” arXiv preprint arXiv:2006.10742, 2020.
[30] Xinlei Chen, et al. “Improved Baselines with Momentum Contrastive Learning” arXiv preprint arXiv:2003.04297, 2020.
[31] Jean-Bastien Grill, et al. “Bootstrap Your Own Latent: A New Approach to Self-Supervised Learning” arXiv preprint arXiv:2006.07733, 2020.
[32] Abe Fetterman & Josh Albrecht. “Understanding self-supervised and contrastive learning with Bootstrap Your Own Latent (BYOL)” Untitled blog. Aug 24, 2020.