Many new Transformer architecture improvements have been proposed since my last post on “The Transformer Family” about three years ago. Here I did a big refactoring and enrichment of that 2020 post — restructure the hierarchy of sections and improve many sections with more recent papers. Version 2.0 is a superset of the old version, about twice the length.
Notations
| Symbol | Meaning |
|---|---|
| $d$ | The model size / hidden state dimension / positional encoding size. |
| $h$ | The number of heads in multi-head attention layer. |
| $L$ | The segment length of input sequence. |
| $N$ | The total number of attention layers in the model; not considering MoE. |
| $\mathbf{X} \in \mathbb{R}^{L \times d}$ | The input sequence where each element has been mapped into an embedding vector of shape $d$, same as the model size. |
| $\mathbf{W}^k \in \mathbb{R}^{d \times d_k}$ | The key weight matrix. |
| $\mathbf{W}^q \in \mathbb{R}^{d \times d_k}$ | The query weight matrix. |
| $\mathbf{W}^v \in \mathbb{R}^{d \times d_v}$ | The value weight matrix. Often we have $d_k = d_v = d$. |
| $\mathbf{W}^k_i, \mathbf{W}^q_i \in \mathbb{R}^{d \times d_k/h}; \mathbf{W}^v_i \in \mathbb{R}^{d \times d_v/h}$ | The weight matrices per head. |
| $\mathbf{W}^o \in \mathbb{R}^{d_v \times d}$ | The output weight matrix. |
| $\mathbf{Q} = \mathbf{X}\mathbf{W}^q \in \mathbb{R}^{L \times d_k}$ | The query embedding inputs. |
| $\mathbf{K} = \mathbf{X}\mathbf{W}^k \in \mathbb{R}^{L \times d_k}$ | The key embedding inputs. |
| $\mathbf{V} = \mathbf{X}\mathbf{W}^v \in \mathbb{R}^{L \times d_v}$ | The value embedding inputs. |
| $\mathbf{q}_i, \mathbf{k}_i \in \mathbb{R}^{d_k}, \mathbf{v}_i \in \mathbb{R}^{d_v}$ | Row vectors in query, key, value matrices, $\mathbf{Q}$, $\mathbf{K}$ and $\mathbf{V}$. |
| $S_i$ | A collection of key positions for the $i$-th query $\mathbf{q}_i$ to attend to. |
| $\mathbf{A} \in \mathbb{R}^{L \times L}$ | The self-attention matrix between a input sequence of lenght $L$ and itself. $\mathbf{A} = \text{softmax}(\mathbf{Q}\mathbf{K}^\top / \sqrt{d_k})$. |
| $a_{ij} \in \mathbf{A}$ | The scalar attention score between query $\mathbf{q}_i$ and key $\mathbf{k}_j$. |
| $\mathbf{P} \in \mathbb{R}^{L \times d}$ | position encoding matrix, where the $i$-th row $\mathbf{p}_i$ is the positional encoding for input $\mathbf{x}_i$. |
Transformer Basics
The Transformer (which will be referred to as “vanilla Transformer” to distinguish it from other enhanced versions; Vaswani, et al., 2017) model has an encoder-decoder architecture, as commonly used in many NMT models. Later simplified Transformer was shown to achieve great performance in language modeling tasks, like in encoder-only BERT or decoder-only GPT.
Attention and Self-Attention
Attention is a mechanism in neural network that a model can learn to make predictions by selectively attending to a given set of data. The amount of attention is quantified by learned weights and thus the output is usually formed as a weighted average.
Self-attention is a type of attention mechanism where the model makes prediction for one part of a data sample using other parts of the observation about the same sample. Conceptually, it feels quite similar to non-local means. Also note that self-attention is permutation-invariant; in other words, it is an operation on sets.
There are various forms of attention / self-attention, Transformer (Vaswani et al., 2017) relies on the scaled dot-product attention: given a query matrix $\mathbf{Q}$, a key matrix $\mathbf{K}$ and a value matrix $\mathbf{V}$, the output is a weighted sum of the value vectors, where the weight assigned to each value slot is determined by the dot-product of the query with the corresponding key:
And for a query and a key vector $\mathbf{q}_i, \mathbf{k}_j \in \mathbb{R}^d$ (row vectors in query and key matrices), we have a scalar score:
where $\mathcal{S}_i$ is a collection of key positions for the $i$-th query to attend to.
See my old post for other types of attention if interested.
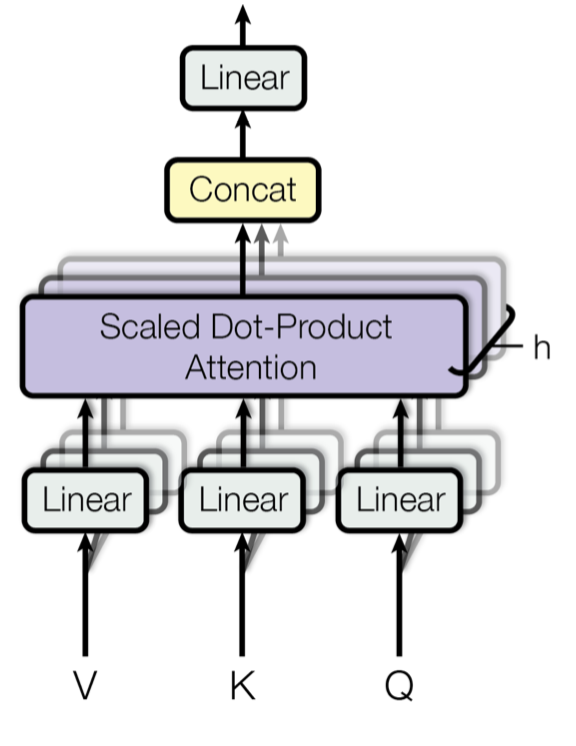
Multi-Head Self-Attention
The multi-head self-attention module is a key component in Transformer. Rather than only computing the attention once, the multi-head mechanism splits the inputs into smaller chunks and then computes the scaled dot-product attention over each subspace in parallel. The independent attention outputs are simply concatenated and linearly transformed into expected dimensions.
where $[.;.]$ is a concatenation operation. $\mathbf{W}^q_i, \mathbf{W}^k_i \in \mathbb{R}^{d \times d_k/h}, \mathbf{W}^v_i \in \mathbb{R}^{d \times d_v/h}$ are weight matrices to map input embeddings of size $L \times d$ into query, key and value matrices. And $\mathbf{W}^o \in \mathbb{R}^{d_v \times d}$ is the output linear transformation. All the weights should be learned during training.
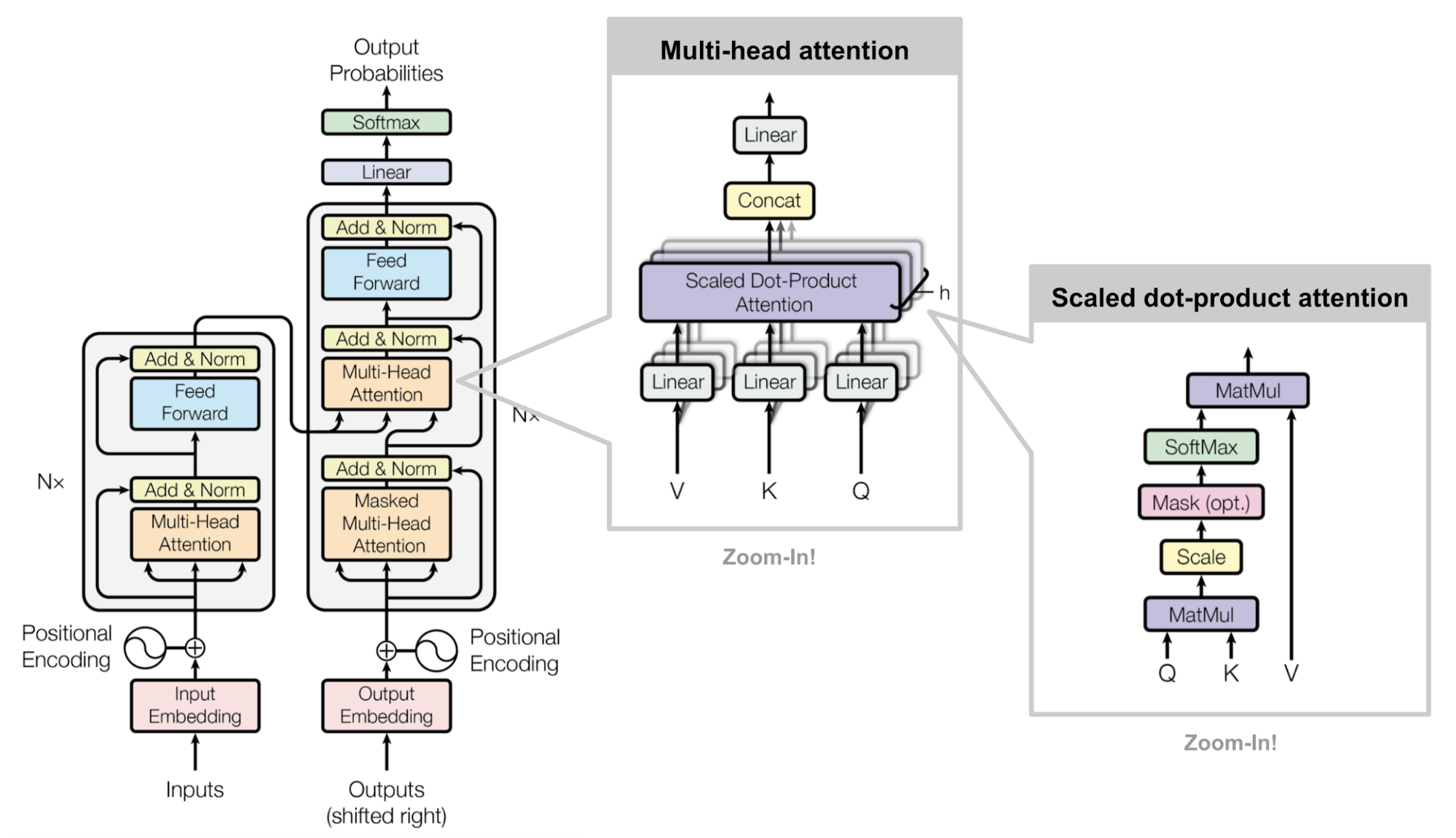
Encoder-Decoder Architecture
The encoder generates an attention-based representation with capability to locate a specific piece of information from a large context. It consists of a stack of 6 identity modules, each containing two submodules, a multi-head self-attention layer and a point-wise fully connected feed-forward network. By point-wise, it means that it applies the same linear transformation (with same weights) to each element in the sequence. This can also be viewed as a convolutional layer with filter size 1. Each submodule has a residual connection and layer normalization. All the submodules output data of the same dimension $d$.
The function of Transformer decoder is to retrieve information from the encoded representation. The architecture is quite similar to the encoder, except that the decoder contains two multi-head attention submodules instead of one in each identical repeating module. The first multi-head attention submodule is masked to prevent positions from attending to the future.
Positional Encoding
Because self-attention operation is permutation invariant, it is important to use proper positional encoding to provide order information to the model. The positional encoding $\mathbf{P} \in \mathbb{R}^{L \times d}$ has the same dimension as the input embedding, so it can be added on the input directly. The vanilla Transformer considered two types of encodings:
Sinusoidal Positional Encoding
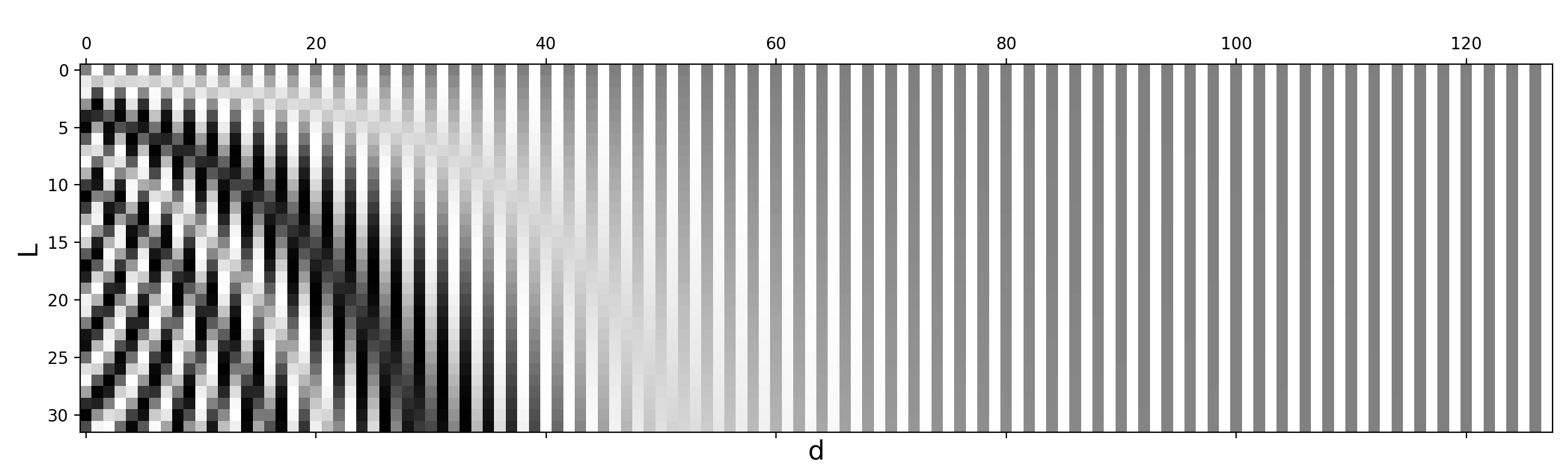
Sinusoidal positional encoding is defined as follows, given the token position $i=1,\dots,L$ and the dimension $\delta=1,\dots,d$:
In this way each dimension of the positional encoding corresponds to a sinusoid of different wavelengths in different dimensions, from $2\pi$ to $10000 \cdot 2\pi$.
Learned Positional Encoding
Learned positional encoding assigns each element with a learned column vector which encodes its absolute position (Gehring, et al. 2017) and furthermroe this encoding can be learned differently per layer (Al-Rfou et al. 2018).
Relative Position Encoding
Shaw et al. (2018)) incorporated relative positional information into $\mathbf{W}^k$ and $\mathbf{W}^v$. Maximum relative position is clipped to a maximum absolute value of $k$ and this clipping operation enables the model to generalize to unseen sequence lengths. Therefore, $2k + 1$ unique edge labels are considered and let us denote $\mathbf{P}^k, \mathbf{P}^v \in \mathbb{R}^{2k+1}$ as learnable relative position representations.
Transformer-XL (Dai et al., 2019) proposed a type of relative positional encoding based on reparametrization of dot-product of keys and queries. To keep the positional information flow coherently across segments, Transformer-XL encodes the relative position instead, as it could be sufficient enough to know the position offset for making good predictions, i.e. $i-j$, between one key vector $\mathbf{k}_{\tau, j}$ and its query $\mathbf{q}_{\tau, i}$.
If omitting the scalar $1/\sqrt{d_k}$ and the normalizing term in softmax but including positional encodings, we can write the attention score between query at position $i$ and key at position $j$ as:
Transformer-XL reparameterizes the above four terms as follows:
- Replace $\mathbf{p}_j$ with relative positional encoding $\mathbf{r}_{i-j} \in \mathbf{R}^{d}$;
- Replace $\mathbf{p}_i\mathbf{W}^q$ with two trainable parameters $\mathbf{u}$ (for content) and $\mathbf{v}$ (for location) in two different terms;
- Split $\mathbf{W}^k$ into two matrices, $\mathbf{W}^k_E$ for content information and $\mathbf{W}^k_R$ for location information.
Rotary Position Embedding
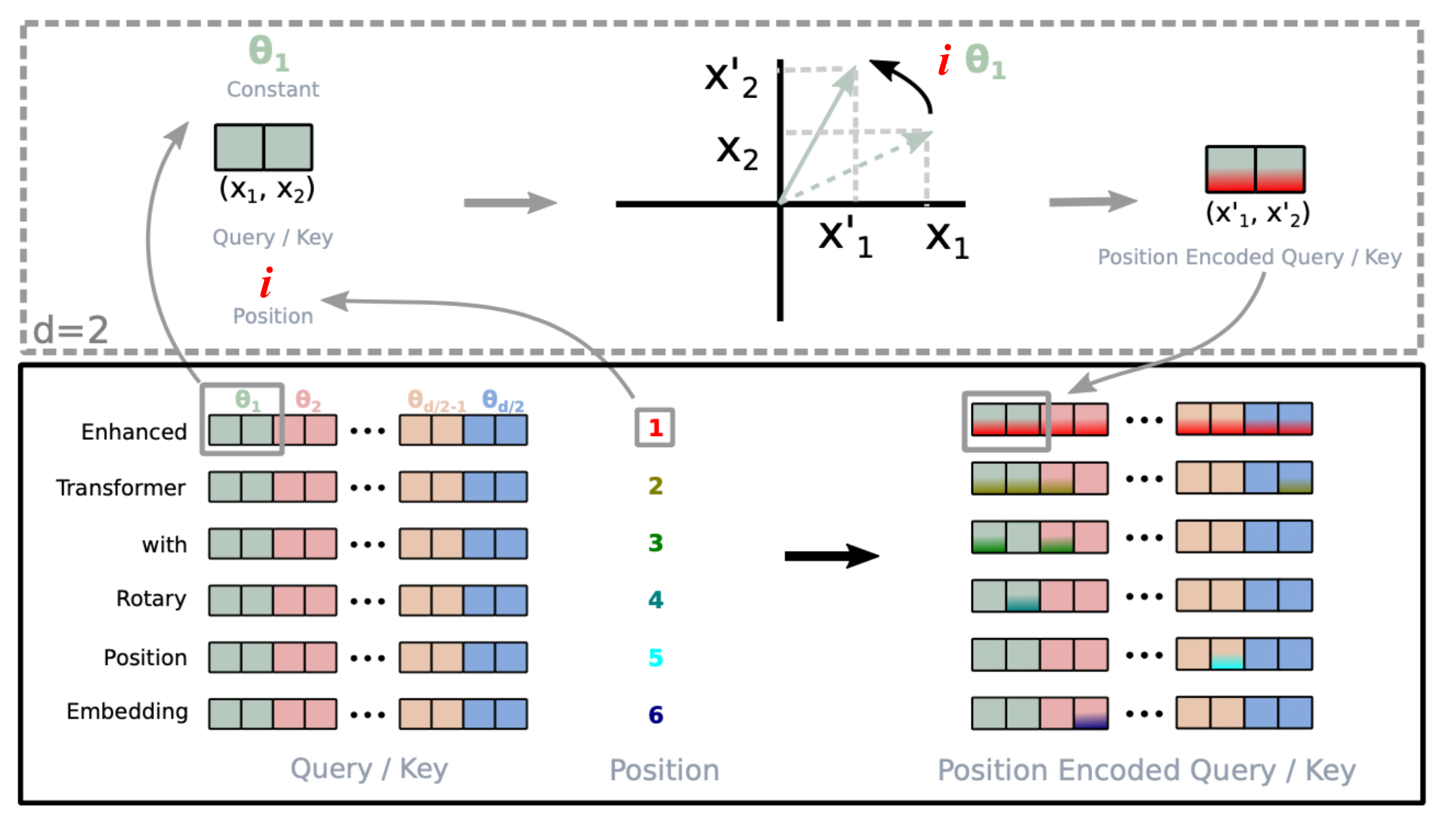
Rotary position embedding (RoPE; Su et al. 2021) encodes the absolution position with a rotation matrix and multiplies key and value matrices of every attention layer with it to inject relative positional information at every layer.
When encoding relative positional information into the inner product of the $i$-th key and the $j$-th query, we would like to formulate the function in a way that the inner product is only about the relative position $i-j$. Rotary Position Embedding (RoPE) makes use of the rotation operation in Euclidean space and frames the relative position embedding as simply rotating feature matrix by an angle proportional to its position index.
Given a vector $\mathbf{z}$, if we want to rotate it counterclockwise by $\theta$, we can multiply it by a rotation matrix to get $R\mathbf{z}$ where the rotation matrix $R$ is defined as:
When generalizing to higher dimensional space, RoPE divide the $d$-dimensional space into $d/2$ subspaces and constructs a rotation matrix $R$ of size $d \times d$ for token at position $i$:
where in the paper we have $\Theta = {\theta_i = 10000^{-2(i−1)/d}, i \in [1, 2, …, d/2]}$. Note that this is essentially equivalent to sinusoidal positional encoding but formulated as a rotation matrix.
Then both key and query matrices incorporates the positional information by multiplying with this rotation matrix:
Longer Context
The length of an input sequence for transformer models at inference time is upper-bounded by the context length used for training. Naively increasing context length leads to high consumption in both time ($\mathcal{O}(L^2d)$) and memory ($\mathcal{O}(L^2)$) and may not be supported due to hardware constraints.
This section introduces several improvements in transformer architecture to better support long context at inference; E.g. using additional memory, design for better context extrapolation, or recurrency mechanism.
Context Memory
The vanilla Transformer has a fixed and limited attention span. The model can only attend to other elements in the same segments during each update step and no information can flow across separated fixed-length segments. This context segmentation causes several issues:
- The model cannot capture very long term dependencies.
- It is hard to predict the first few tokens in each segment given no or thin context.
- The evaluation is expensive. Whenever the segment is shifted to the right by one, the new segment is re-processed from scratch, although there are a lot of overlapped tokens.
Transformer-XL (Dai et al., 2019; “XL” means “extra long”) modifies the architecture to reuse hidden states between segments with an additional memory. The recurrent connection between segments is introduced into the model by continuously using the hidden states from the previous segments.
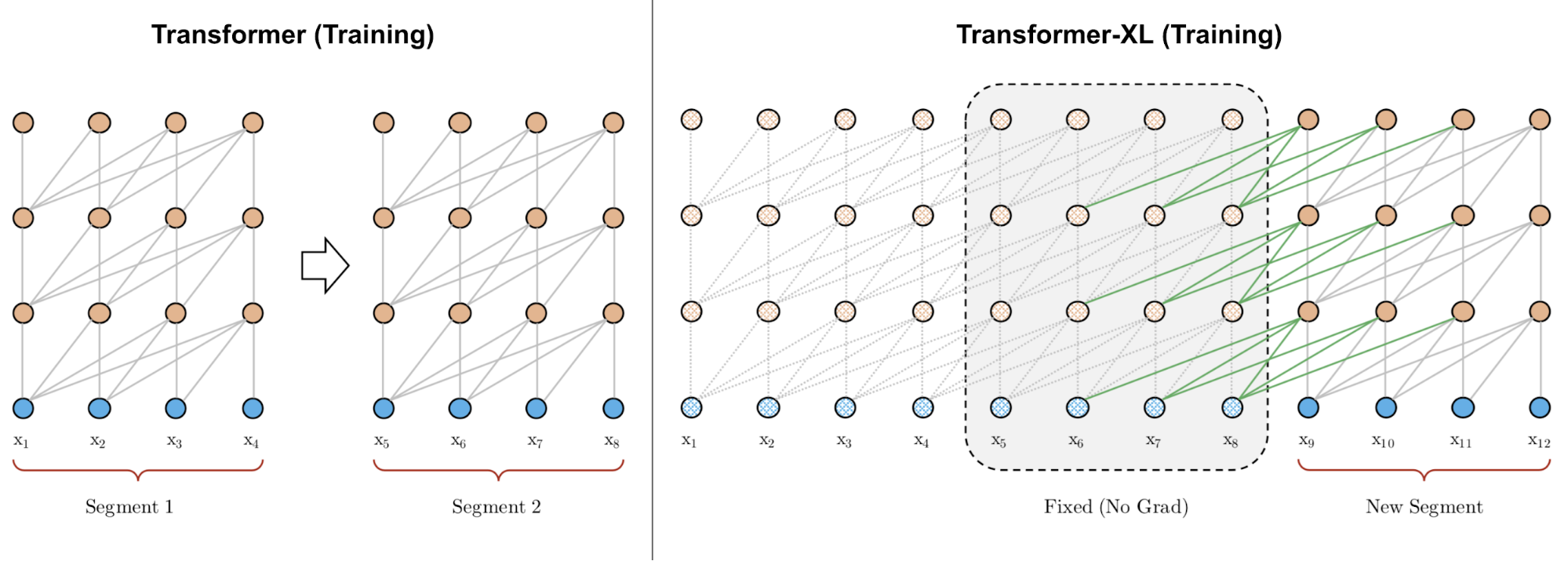
Let’s label the hidden state of the $n$-th layer for the $(\tau + 1)$-th segment in the model as $\mathbf{h}_{\tau+1}^{(n)} \in \mathbb{R}^{L \times d}$. In addition to the hidden state of the last layer for the same segment $\mathbf{h}_{\tau+1}^{(n-1)}$, it also depends on the hidden state of the same layer for the previous segment $\mathbf{h}_{\tau}^{(n)}$. By incorporating information from the previous hidden states, the model extends the attention span much longer in the past, over multiple segments.
Note that both keys and values rely on extended hidden states, while queries only consume hidden states at the current step. The concatenation operation $[. \circ .]$ is along the sequence length dimension. And Transformer-XL needs to use relative positional encoding because previous and current segments would be assigned with the same encoding if we encode absolute positions, which is undesired.
Compressive Transformer (Rae et al. 2019) extends Transformer-XL by compressing past memories to support longer sequences. It explicitly adds memory slots of size $m_m$ per layer for storing past activations of this layer to preserve long context. When some past activations become old enough, they are compressed and saved in an additional compressed memory of size $m_{cm}$ per layer.
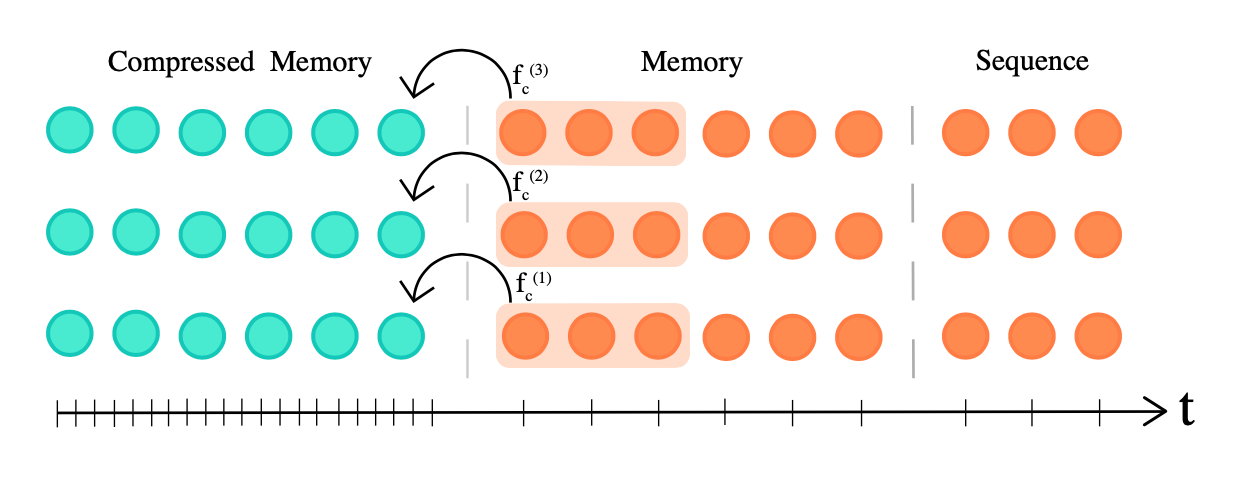
Both memory and compressed memory are FIFO queues. Given the model context length $L$, the compression function of compression rate $c$ is defined as $f_c: \mathbb{R}^{L \times d} \to \mathbb{R}^{[\frac{L}{c}] \times d}$, mapping $L$ oldest activations to $[\frac{L}{c}]$ compressed memory elements. There are several choices of compression functions:
- Max/mean pooling of kernel and stride size $c$;
- 1D convolution with kernel and stride size $c$ (need to learn additional parameters);
- Dilated convolution (need to learn additional parameters). In their experiments, convolution compression works out the best on
EnWik8dataset; - Most used memories.
Compressive transformer has two additional training losses:
-
Auto-encoding loss (lossless compression objective) measures how well we can reconstruct the original memories from compressed memories
$$ \mathcal{L}_{ac} = \| \textbf{old_mem}^{(i)} - g(\textbf{new_cm}^{(i)}) \|_2 $$where $g: \mathbb{R}^{[\frac{L}{c}] \times d} \to \mathbb{R}^{L \times d}$ reverses the compression function $f$. -
Attention-reconstruction loss (lossy objective) reconstructs content-based attention over memory vs compressed memory and minimize the difference:
$$ \mathcal{L}_{ar} = \|\text{attn}(\mathbf{h}^{(i)}, \textbf{old_mem}^{(i)}) − \text{attn}(\mathbf{h}^{(i)}, \textbf{new_cm}^{(i)})\|_2 $$
Transformer-XL with a memory of size $m$ has a maximum temporal range of $m \times N$, where $N$ is the number of layers in the model, and attention cost $\mathcal{O}(L^2 + Lm)$. In comparison, compressed transformer has a temporal range of $(m_m + c \cdot m_{cm}) \times N$ and attention cost $\mathcal{O}(L^2 + L(m_m + m_{cm}))$. A larger compression rate $c$ gives better tradeoff between temporal range length and attention cost.
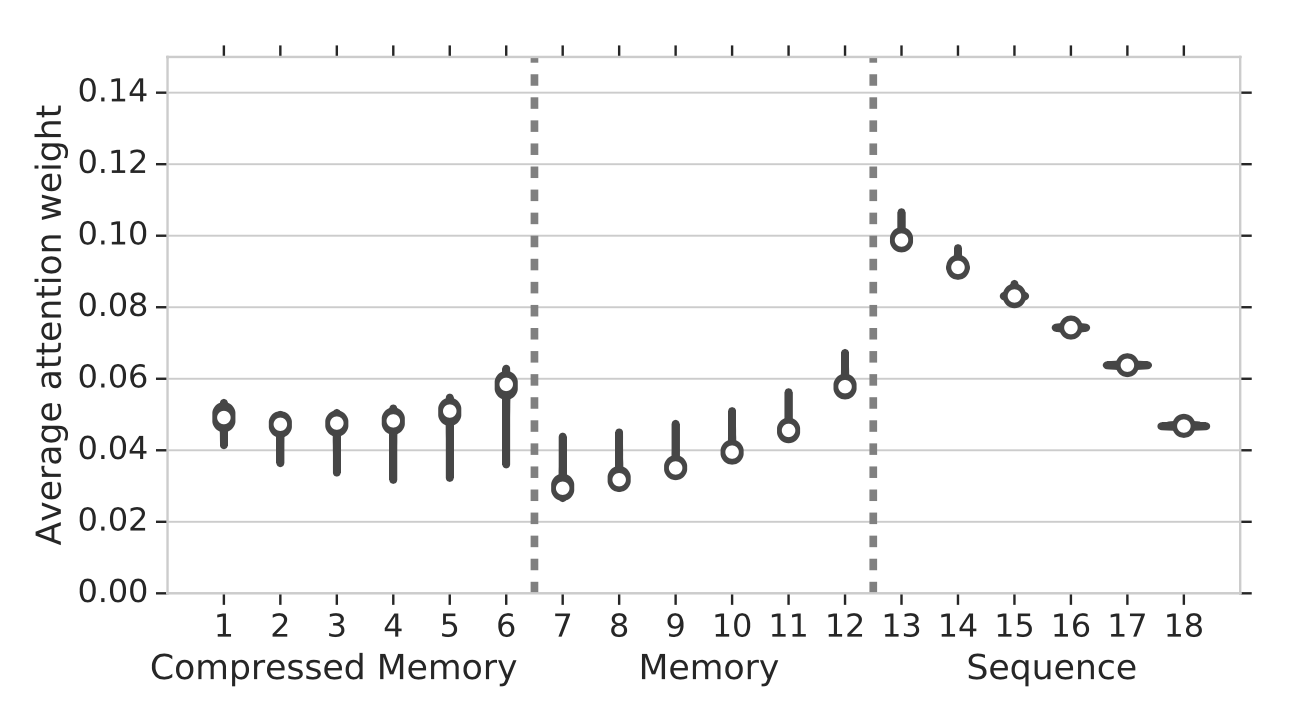
Attention weights, from oldest to newest, are stored in three locations: compressed memory → memory → causally masked sequence. In the experiments, they observed an increase in attention weights from oldest activations stored in the regular memory, to activations stored in the compressed memory, implying that the network is learning to preserve salient information.
Non-Differentiable External Memory
$k$NN-LM (Khandelwal et al. 2020) enhances a pretrained LM with a separate $k$NN model by linearly interpolating the next token probabilities predicted by both models. The $k$NN model is built upon an external key-value store which can store any large pre-training dataset or OOD new dataset. This datastore is preprocessed to save a large number of pairs, (LM embedding representation of context, next token) and the nearest neighbor retrieval happens in the LM embedding space. Because the datastore can be gigantic, we need to rely on libraries for fast dense vector search such as FAISS or ScaNN. The indexing process only happens once and parallelism is easy to implement at inference time.
At inference time, the next token probability is a weighted sum of two predictions:
where $\mathcal{N}$ contains a set of nearest neighbor data points retrieved by $k$NN; $d(., .)$ is a distance function such as L2 distance.
According to the experiments, larger datastore size or larger $k$ is correlated with better perplexity. The weighting scalar $\lambda$ should be tuned, but in general it is expected to be larger for out-of-domain data compared to in-domain data and larger datastore can afford a larger $\lambda$.
SPALM (Adaptive semiparametric language models; Yogatama et al. 2021) incorporates both (1) Transformer-XL style memory for hidden states from external context as short-term memory and (2) $k$NN-LM style key-value store as long memory.
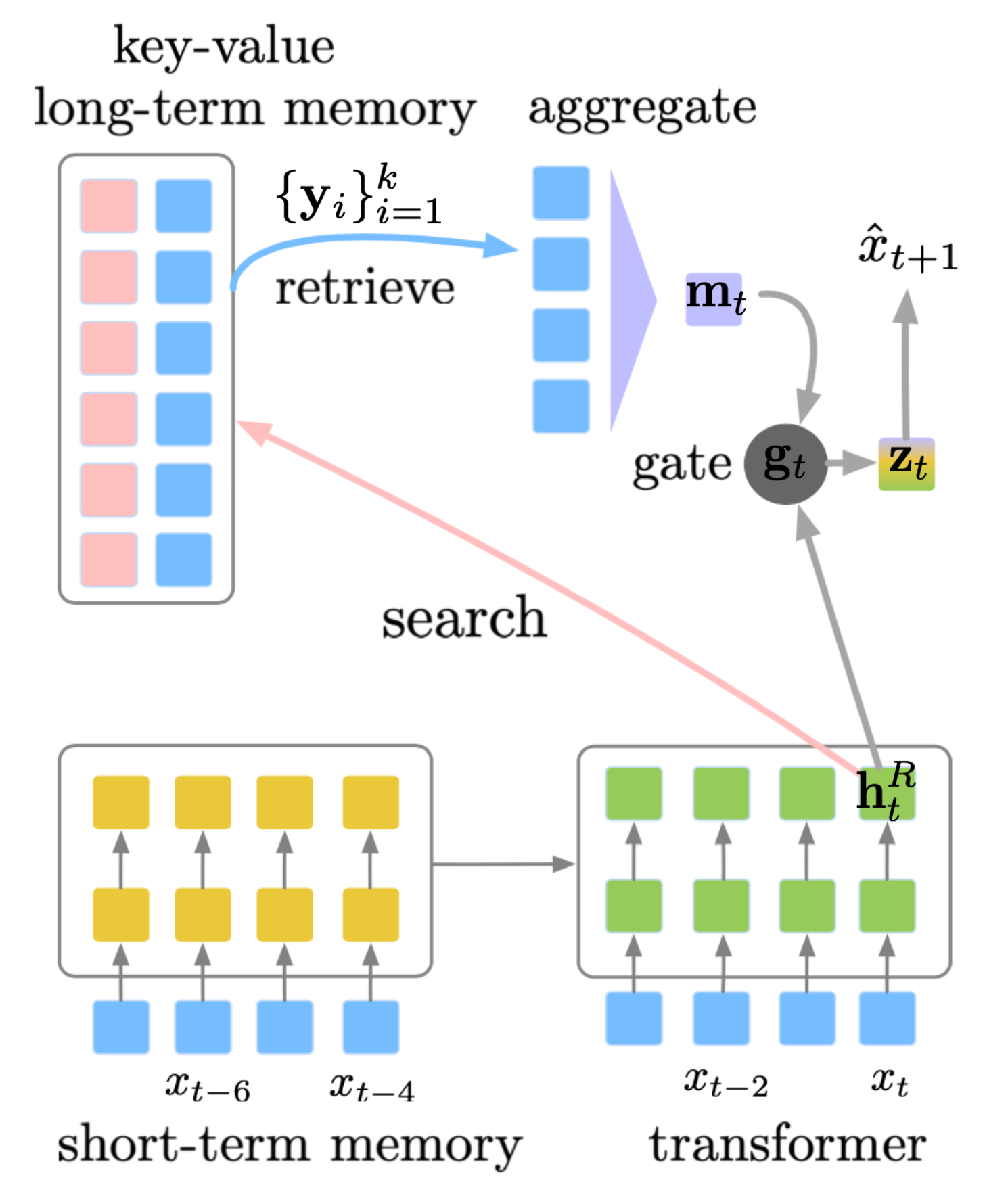
SPALM runs $k$NN search to fetch $k$ tokens with most relevant context. For each token we can get the same embedding representation provided by a pretrained LM, denoted as $\{\mathbf{y}_i\}_{i=1}^k$. The gating mechanism first aggregates the retrieved token embeddings with a simple attention layer using $\mathbf{h}^R_t$ (the hidden state for token $x_t$ at layer $R$) as a query and then learns a gating parameter $\mathbf{g}_t$ to balance between local information $\mathbf{h}^R_t$ and long-term information $\mathbf{m}_t$.
where $\mathbf{w}_g$ is a parameter vector to learn; $\sigma(.)$ is sigmoid; $\mathbf{W}$ is the word embedding matrix shared between both input and output tokens. Different from $k$NN-LM, they didn’t find the nearest neighbor distance to be helpful in the aggregation of retrieved tokens.
During training, the key representations in the long-term memory stay constant, produced by a pretrained LM, but the value encoder, aka the word embedding matrix, gets updated.
Memorizing Transformer (Wu et al. 2022) adds a $k$NN-augmented attention layer near the top stack of a decoder-only Transformer. This special layer maintains a Transformer-XL style FIFO cache of past key-value pairs.
The same QKV values are used for both local attention and $k$NN mechanisms. The $k$NN lookup returns top-$k$ (key, value) pairs for each query in the input sequence and then they are processed through the self-attention stack to compute a weighted average of retrieved values. Two types of attention are combined with a learnable per-head gating parameter. To prevent large distributional shifts in value magnitude, both keys and values in the cache are normalized.
What they found during experiments with Memorizing Transformer:
- It is observed in some experiments that training models with a small memory and then finetuned with a larger memory works better than training with a large memory from scratch.
- The smaller Memorizing Transformer with just 8k tokens in memory can match the perplexity of a larger vanilla Transformer with 5X more trainable parameters.
- Increasing the size of external memory provided consistent gains up to a size of 262K.
- A non-memory transformer can be finetuned to use memory.
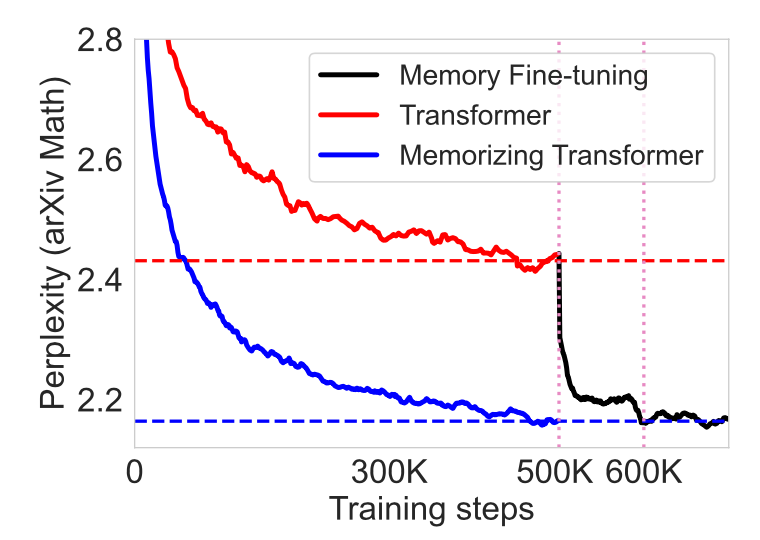
Distance-Enhanced Attention Scores
Distance Aware Transformer(DA-Transformer; Wu, et al. 2021) and Attention with Linear Biases (ALiBi; Press et al. 2022) are motivated by similar ideas — in order to encourage the model to extrapolate over longer context than what the model is trained on, we can explicitly attach the positional information to every pair of attention score based on the distance between key and query tokens.
Note that the default positional encoding in vanilla Transformer only adds positional information to the input sequence, while later improved encoding mechanisms alter attention scores of every layer, such as rotary position embedding, and they take on form very similar to distance enhanced attention scores.
DA-Transformer (Wu, et al. 2021) multiplies attention scores at each layer by a learnable bias that is formulated as a function of the distance between key and query. Different attention heads use different parameters to distinguish diverse preferences to short-term vs long-term context. Given two positions, $i, j$, DA-Transformer uses the following weighting function to alter the self-attention score:
where $\alpha_i$ is a learnable parameters to weight relative distance differently per head where the head is indexed by superscript $^{(i)}$; $\beta_i$ is a learnable parameter to control the upper bound and ascending slope wrt the distance for the $i$-th attention head. The weighting function $f(.)$ is designed in a way that: (1) $f(0)=1$; (2) $f(\mathbf{R}^{(i)}) = 0$ when $\mathbf{R}^{(i)} \to -\infty$; (3) $f(\mathbf{R}^{(i)})$ is bounded when $\mathbf{R}^{(i)} \to +\infty$; (4) the scale is tunable; (5) and the function is monotonic. The extra time complexity brought by $f(\mathbf{R}^{(i)})$ is $\mathcal{O}(L^2)$ and it is small relative to the self attention time complexity $\mathcal{O}(L^2 d)$. The extra memory consumption is minimal, ~$\mathcal{O}(2h)$.
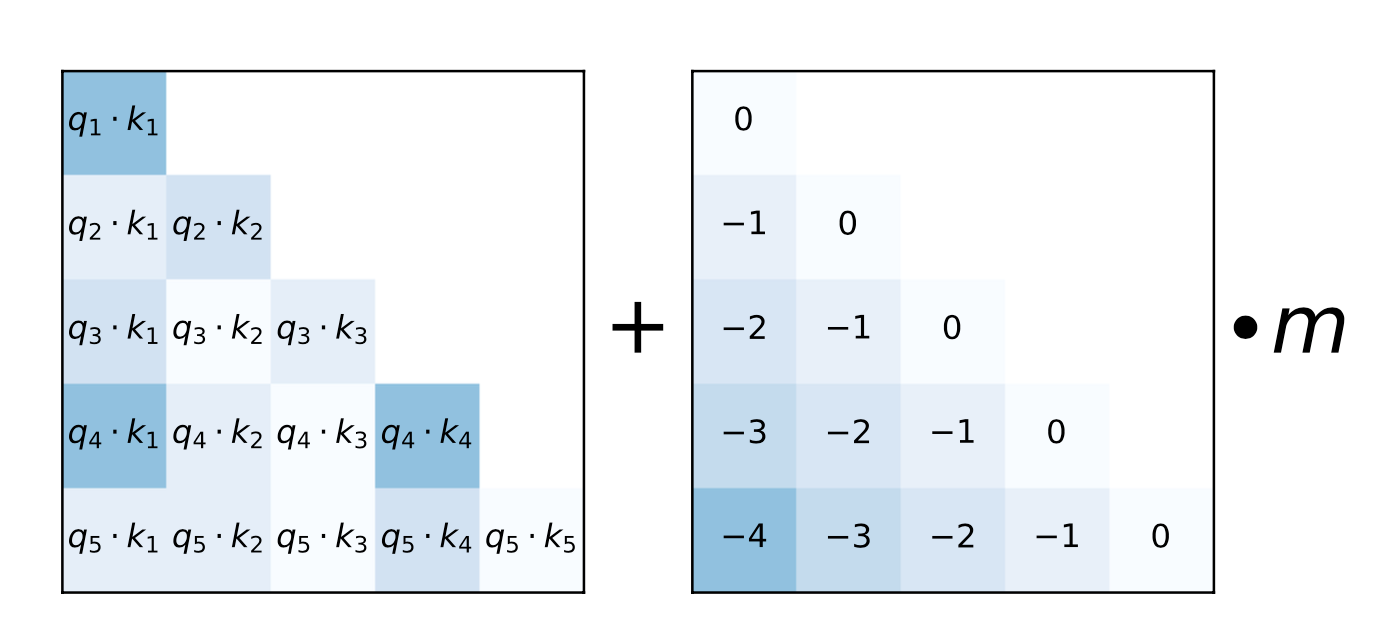
Instead of multipliers, ALiBi (Press et al. 2022) adds a constant bias term on query-key attention scores, proportional to pairwise distances. The bias introduces a strong recency preference and penalizes keys that are too far away. The penalties are increased at different rates within different heads. $$ \text{softmax}(\mathbf{q}_i \mathbf{K}^\top + \alpha_i \cdot [0, -1, -2, \dots, -(i-1)]) $$ where $\alpha_i$ is a head-specific weighting scalar. Different from DA-transformer, $\alpha_i$ is not learned but fixed as a geometric sequence; for example, for 8 heads, ${\alpha_i} = {\frac{1}{2}, \frac{1}{2^2}, \dots, \frac{1}{2^8}}$. The overall idea is very much similar to what relative positional encoding aims to solve.
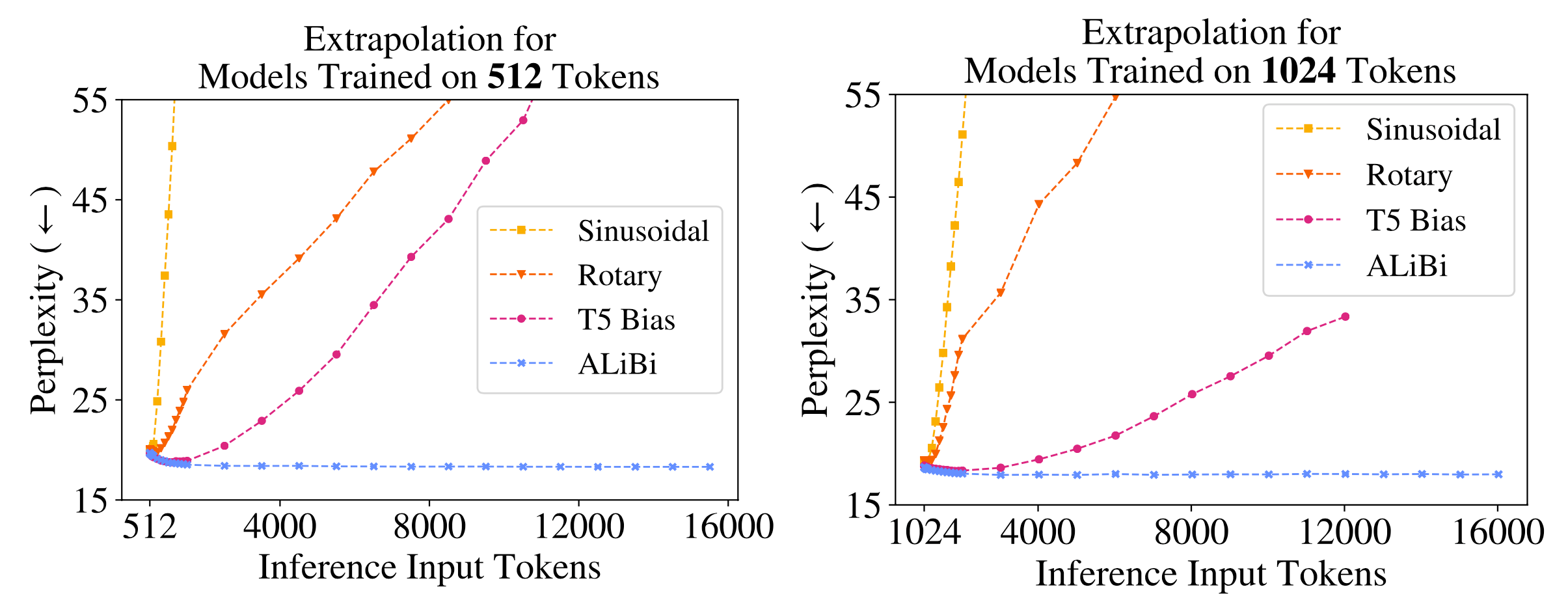
With ALiBi, Press et al. (2022) trained a 1.3B model on context length 1024 during training and extrapolated to 2046 at inference time.
Make it Recurrent
Universal Transformer (Dehghani, et al. 2019) combines self-attention in Transformer with the recurrent mechanism in RNN, aiming to benefit from both a long-term global receptive field of Transformer and learned inductive biases of RNN. Rather than going through a fixed number of layers, Universal Transformer dynamically adjusts the number of steps using adaptive computation time. If we fix the number of steps, an Universal Transformer is equivalent to a multi-layer Transformer with shared parameters across layers.
On a high level, the universal transformer can be viewed as a recurrent function for learning the hidden state representation per token. The recurrent function evolves in parallel across token positions and the information between positions is shared through self-attention.
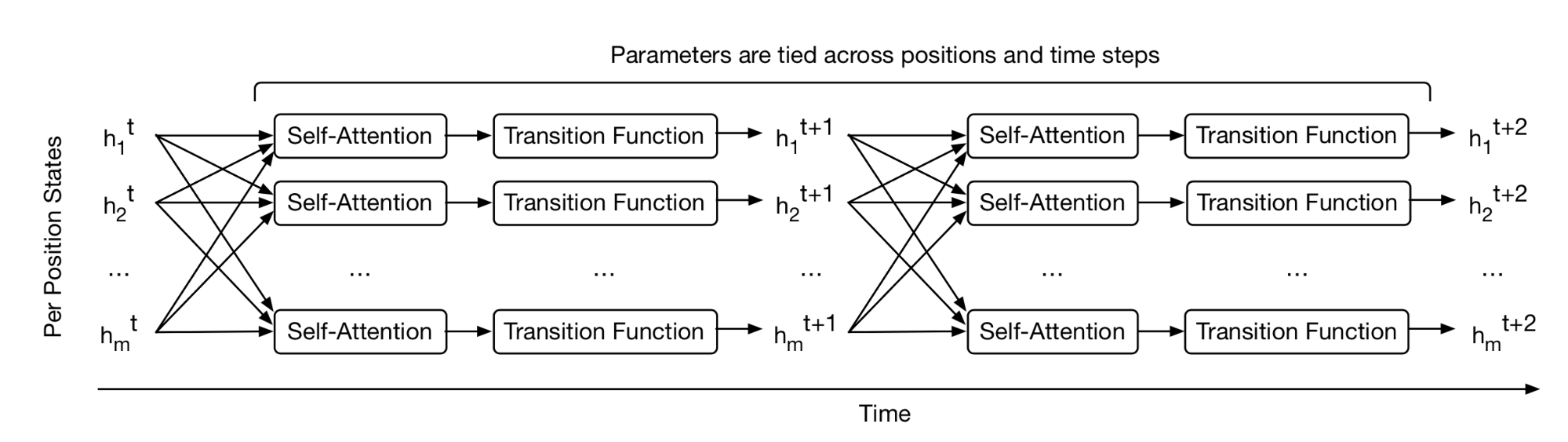
Given an input sequence of length $L$, Universal Transformer iteratively updates the representation $\mathbf{h}^t \in \mathbb{R}^{L \times d}$ at step $t$ for an adjustable number of steps. At step 0, $\mathbf{h}^0$ is initialized to be same as the input embedding matrix. All the positions are processed in parallel in the multi-head self-attention mechanism and then go through a recurrent transition function.
where $\text{Transition}(.)$ is either a separable convolution or a fully-connected neural network that consists of two position-wise (i.e. applied to each row of $\mathbf{A}^t$ individually) affine transformation + one ReLU.
The positional encoding $\mathbf{P}^t$ uses sinusoidal position signal but with an additional time dimension:
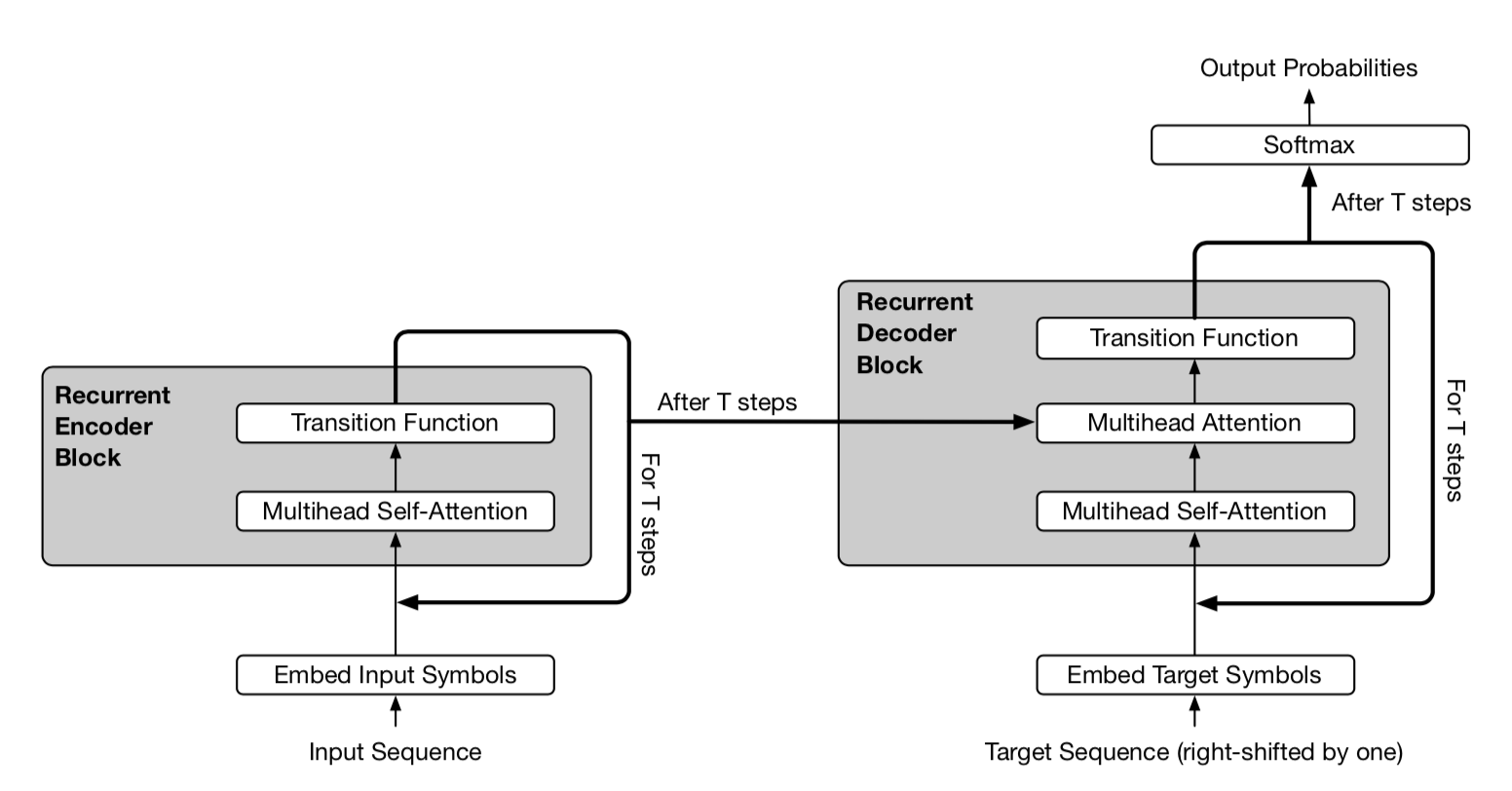
In the adaptive version of Universal Transformer, the number of recurrent steps $T$ is dynamically determined by ACT. Each position is equipped with a dynamic ACT halting mechanism. Once a per-token recurrent block halts, it stops taking more recurrent updates but simply copies the current value to the next step until all the blocks halt or until the model reaches a maximum step limit.
Adaptive Modeling
Adaptive modeling refers to a mechanism that can adjust the amount of computation according to different inputs. For example, some tokens may only need local information and thus demand a shorter attention span; Or some tokens are relatively easier to predict and do not need to be processed through the entire attention stack.
Adaptive Attention Span
One key advantage of Transformer is the capability of capturing long-term dependencies. Depending on the context, the model may prefer to attend further sometime than others; or one attention head may had different attention pattern from the other. If the attention span could adapt its length flexibly and only attend further back when needed, it would help reduce both computation and memory cost to support longer maximum context size in the model.
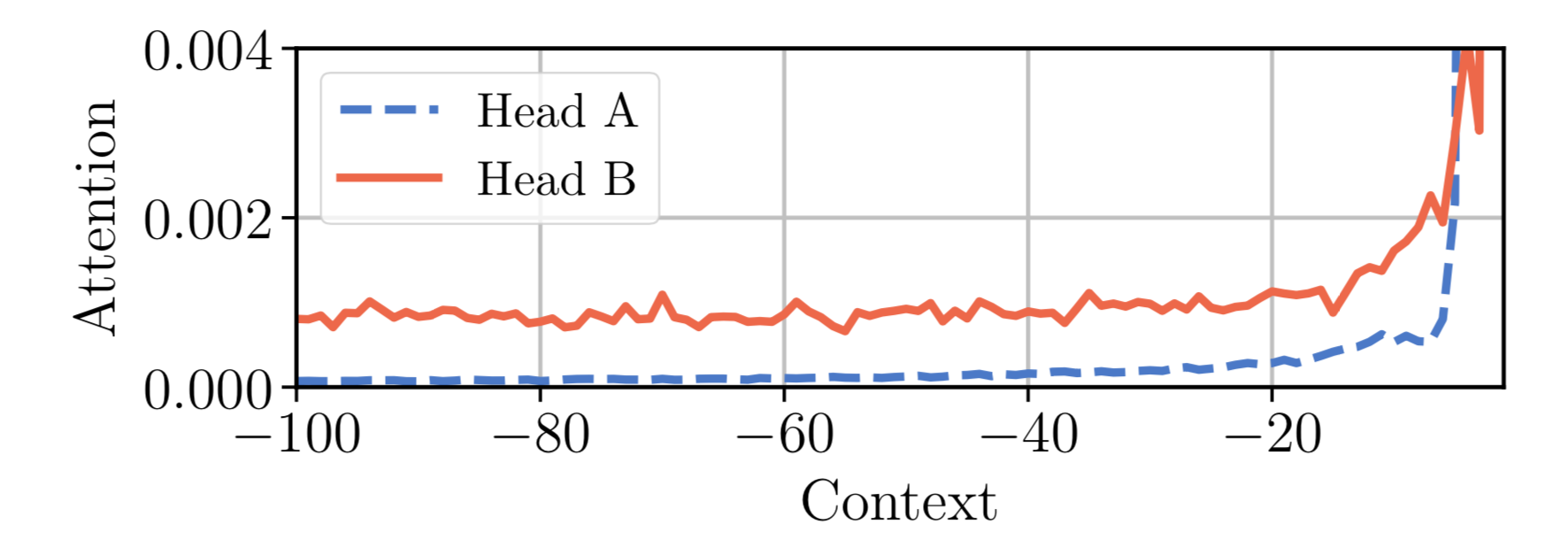
This is the motivation for Adaptive Attention Span. Sukhbaatar et al (2019) proposed a self-attention mechanism that seeks an optimal attention span. They hypothesized that different attention heads might assign scores differently within the same context window (See Fig. 14) and thus the optimal span would be trained separately per head.
Given the $i$-th token, we need to compute the attention weights between this token and other keys within its attention span of size $s$:
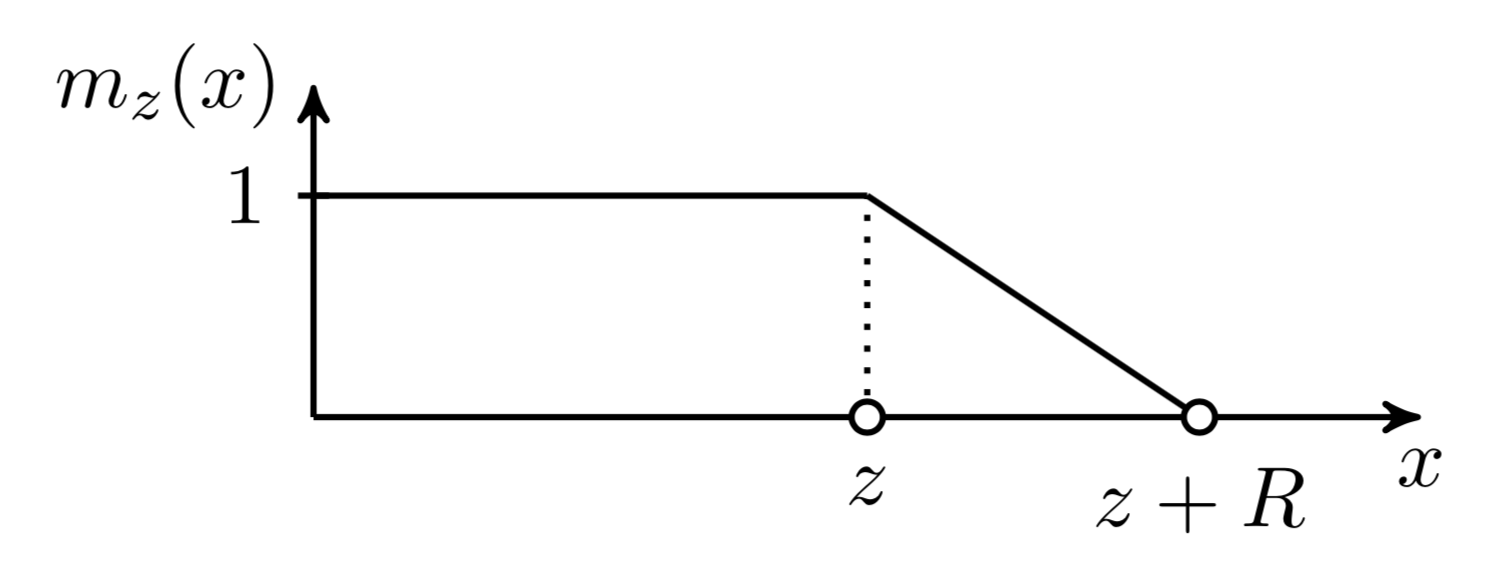
A soft mask function $m_z$ is added to control for an effective adjustable attention span, which maps the distance between query and key into a [0, 1] value. $m_z$ is parameterized by $z \in [0, s]$ and $z$ is to be learned:
where $R$ is a hyper-parameter which defines the softness of $m_z$.
The soft mask function is applied to the softmax elements in the attention weights:
In the above equation, $z$ is differentiable so it is trained jointly with other parts of the model. Parameters $z^{(i)}, i=1, \dots, h$ are learned separately per head. Moreover, the loss function has an extra L1 penalty on $\sum_{i=1}^h z^{(i)}$.
Using Adaptive Computation Time, the approach can be further enhanced to have flexible attention span length, adaptive to the current input dynamically. The span parameter $z_t$ of an attention head at time $t$ is a sigmoidal function, $z_t = S \sigma(\mathbf{v} \cdot \mathbf{x}_t +b)$, where the vector $\mathbf{v}$ and the bias scalar $b$ are learned jointly with other parameters.
In the experiments of Transformer with adaptive attention span, Sukhbaatar, et al. (2019) found a general tendency that lower layers do not require very long attention spans, while a few attention heads in higher layers may use exceptionally long spans. Adaptive attention span also helps greatly reduce the number of FLOPS, especially in a big model with many attention layers and a large context length.
Depth-Adaptive Transformer
At inference time, it is natural to assume that some tokens are easier to predict and thus do not require as much computation as others. Therefore we may only process its prediction through a limited number of layers to achieve a good balance between speed and performance.
Both Depth-Adaptive Transformer (Elabyad et al. 2020) and Confident Adaptive Language Model (CALM; Schuster et al. 2022) are motivated by this idea and learn to predict optimal numbers of layers needed for different input tokens.
Depth-adaptive transformer (Elabyad et al. 2020) attaches an output classifier to every layer to produce exit predictions based on activations of that layer. The classifier weight matrices can be different per layer or shared across layers. During training, the model sample different sequences of exits such that the model is optimized with hidden states of different layers. The learning objective incorporates likelihood probabilities predicted at different layers, $n=1, \dots, N$:
Adaptive depth classifiers outputs a parametric distribution $q_t$. It is trained with cross entropy loss against an oracle distribution $q^*_t$. The paper explored three confiurations for how to learn such a classifier $q_t$.
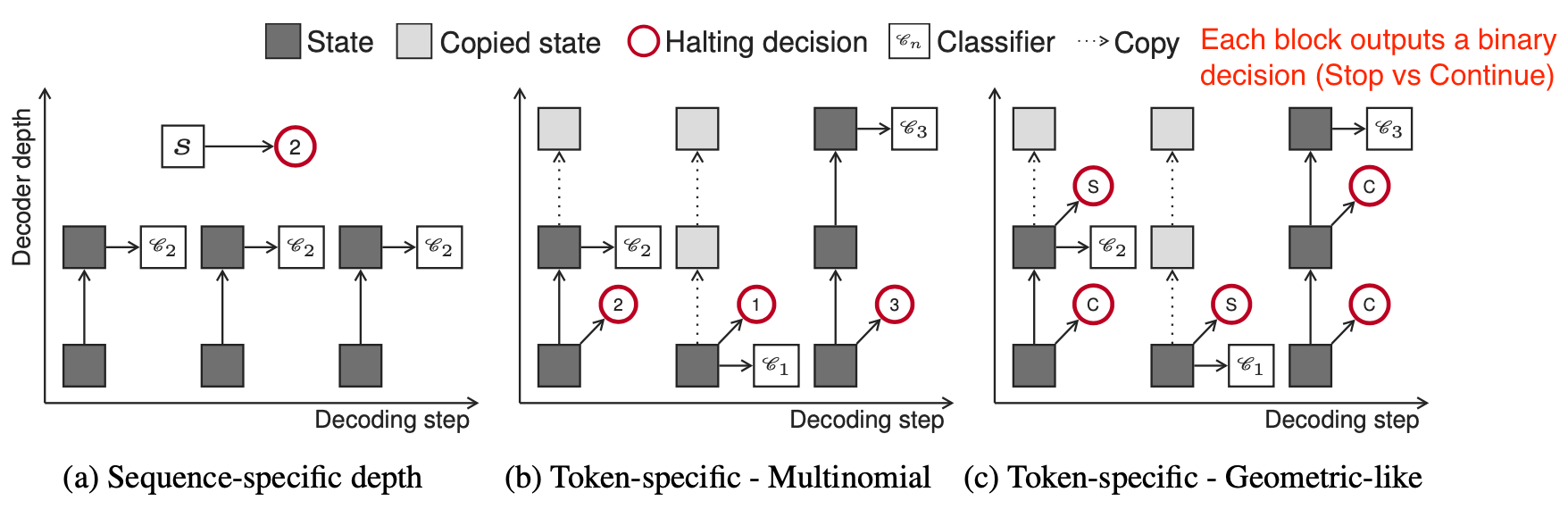
(Image source: Elabyad et al. 2020).
-
Sequence-specific depth classifier: All tokens of the same sequence share the same exit block. It depends on the average of the encoder representation of the sequence. Given an input sequence $\mathbf{x}$ of length $L$, the classifier takes $\bar{\mathbf{x}} = \frac{1}{L} \sum_{t=1}^L \mathbf{x}_t$ as input and outputs a multinomial distribution of $N$ dimensions, corresponding to $N$ layers.
$$ \begin{aligned} q(n \vert \mathbf{x}) &=\text{softmax}(\mathbf{W}_n \bar{\mathbf{x}} + b_n) \in \mathbb{R}^N \\ q_\text{lik}^*(\mathbf{x}, \mathbf{y}) &= \delta(\arg\max_n \text{LL}^n - \lambda n) \\ \text{or }q_\text{corr}^*(\mathbf{x}, \mathbf{y}) &= \delta(\arg\max_n C^n - \lambda n) \text{ where }C^n = \vert\{t \vert y_t = \arg\max_y p(y \vert \mathbf{h}^n_{t-1})\}\vert \\ \end{aligned} $$where $\delta$ is dirac delta (unit impulse) function and $-\lambda n$ is a regularization term to encourage lower layer exits. The ground truth $q^*$ can be prepared in two way, based on maximum likelihood $q_\text{lik}^*$ or correctness $q_\text{corr}^*$.
-
Token-specific depth classifier (multinomial): Each token is decoded with different exit block, predicted conditioned on the first decoder hidden state $\mathbf{h}^1_t$:
$$ q_t(n \vert \mathbf{x}, \mathbf{y}_{< t}) = \text{softmax}(\mathbf{W}_n \mathbf{h}^1_t + b_n) $$
-
Token-specific depth classifier (geometric-like): A binary exit prediction distribution is made per layer per token, $\mathcal{X}^n_t$. The RBF kernel $\kappa(t, t’) = \exp(\frac{\vert t - t’ \vert^2}{\sigma})$ is used to smooth the predictions to incorporate the impact of current decision on future time steps.
$$ \begin{aligned} \mathcal{X}^n_t &= \text{sigmoid}(\mathbf{w}_n^\top \mathbf{h}^n_t + b_n)\quad \forall n \in [1, \dots, N-1] \\ q_t(n \vert \mathbf{x}, \mathbf{y}_{< t}) &= \begin{cases} \mathcal{X}^n_t \prod_{n' < n} (1 - \mathcal{X}^{n'}_t) & \text{if } n < N\\ \prod_{n' < N} (1 - \mathcal{X}^{n'}_t) & \text{otherwise} \end{cases} \\ q_\text{lik}^*(\mathbf{x}, \mathbf{y}) &= \delta(\arg\max_n \widetilde{\text{LL}}^n_t - \lambda n) \text{ where } \widetilde{\text{LL}}^n_t = \sum_{t'=1}^{\vert\mathbf{y}\vert}\kappa(t, t') LL^n_{t'} \\ \text{or }q_\text{cor}^*(\mathbf{x}, \mathbf{y}) &= \delta(\arg\max_n \tilde{C}_t^n - \lambda n) \text{ where }C_t^n = \mathbb{1}[y_t = \arg\max_y p(y \vert \mathbf{h}^n_{t-1})],\; \tilde{C}^n_t = \sum_{t'=1}^{\vert\mathbf{y}\vert}\kappa(t, t') C^n_{t'} \\ \end{aligned} $$
At inference time, the confidence threshold for making an exit decision needs to be calibrated. Depth-adaptive transformer finds such a threshold on a validation set via grid search. CALM (Schuster et al. 2022) applied the Learn then Test (LTT) framework (Angelopoulos et al. 2021) to identify a subset of valid thresholds and chose the minimum value as the threshold for inference. Except for training per-layer exit classifier, CALM also explored other methods for adaptive depth prediction, including the softmax responses (i.e. difference between top two softmax outputs) and hidden state saturation (i.e. $\cos(\mathbf{h}^n_t, \mathbf{h}^{n+1}_t)$) as confidence scores for exit decisions. They found softmax responses result in best inference speedup.
Efficient Attention
The computation and memory cost of the vanilla Transformer grows quadratically with sequence length and hence it is hard to be applied on very long sequences. Many efficiency improvements for Transformer architecture have something to do with the self-attention module - making it cheaper, smaller or faster to run. See the survey paper on Efficient Transformers (Tay et al. 2020).
Sparse Attention Patterns
Fixed Local Context
A simple alternation to make self-attention less expensive is to restrict the attention span of each token to local context only, so that self-attention grows linearly with the sequence length.
The idea was introduced by Image Transformer (Parmer, et al 2018), which formulates image generation as sequence modeling using an encoder-decoder transformer architecture:
- The encoder generates a contextualized, per-pixel-channel representation of the source image;
- Then the decoder autoregressively generates an output image, one channel per pixel at each time step.
Let’s label the representation of the current pixel to be generated as the query $\mathbf{q}$. Other positions whose representations will be used for computing $\mathbf{q}$ are key vector $\mathbf{k}_1, \mathbf{k}_2, \dots$ and they together form a memory matrix $\mathbf{M}$. The scope of $\mathbf{M}$ defines the context window for pixel query $\mathbf{q}$.
Image Transformer introduced two types of localized $\mathbf{M}$, as illustrated below.
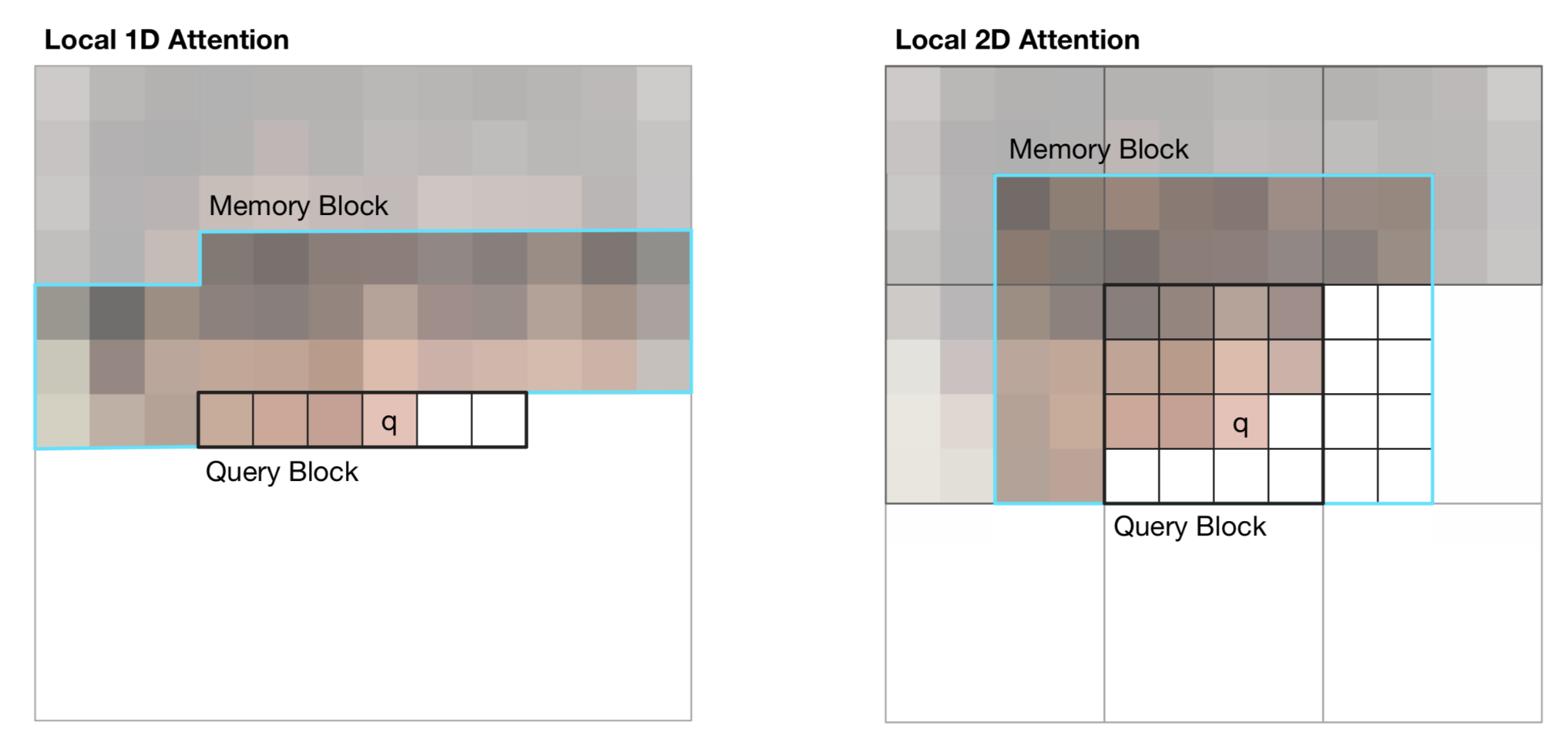
-
1D Local Attention: The input image is flattened in the raster scanning order, that is, from left to right and top to bottom. The linearized image is then partitioned into non-overlapping query blocks. The context window consists of pixels in the same query block as $\mathbf{q}$ and a fixed number of additional pixels generated before this query block.
-
2D Local Attention: The image is partitioned into multiple non-overlapping rectangular query blocks. The query pixel can attend to all others in the same memory blocks. To make sure the pixel at the top-left corner can also have a valid context window, the memory block is extended to the top, left and right by a fixed amount, respectively.
Strided Context
Sparse Transformer (Child et al., 2019) introduced factorized self-attention, through sparse matrix factorization, making it possible to train dense attention networks with hundreds of layers on sequence length up to 16,384, which would be infeasible on modern hardware otherwise.
Given a set of attention connectivity pattern $\mathcal{S} = \{S_1, \dots, S_n\}$, where each $S_i$ records a set of key positions that the $i$-th query vector attends to.
Note that although the size of $S_i$ is not fixed, $a(\mathbf{x}_i, S_i)$ is always of size $d_v$ and thus $\text{Attend}(\mathbf{X}, \mathcal{S}) \in \mathbb{R}^{L \times d_v}$.
In auto-regressive models, one attention span is defined as $S_i = \{j: j \leq i\}$ as it allows each token to attend to all the positions in the past.
In factorized self-attention, the set $S_i$ is decomposed into a tree of dependencies, such that for every pair of $(i, j)$ where $j \leq i$, there is a path connecting $i$ back to $j$ and $i$ can attend to $j$ either directly or indirectly.
Precisely, the set $S_i$ is divided into $p$ non-overlapping subsets, where the $m$-th subset is denoted as $A^{(m)}_i \subset S_i, m = 1,\dots, p$. Therefore the path between the output position $i$ and any $j$ has a maximum length $p + 1$. For example, if $(j, a, b, c, \dots, i)$ is a path of indices between $i$ and $j$, we would have $j \in A_a^{(1)}, a \in A_b^{(2)}, b \in A_c^{(3)}, \dots$, so on and so forth.
Sparse Factorized Attention
Sparse Transformer proposed two types of fractorized attention. It is easier to understand the concepts as illustrated in Fig. 10 with 2D image inputs as examples.
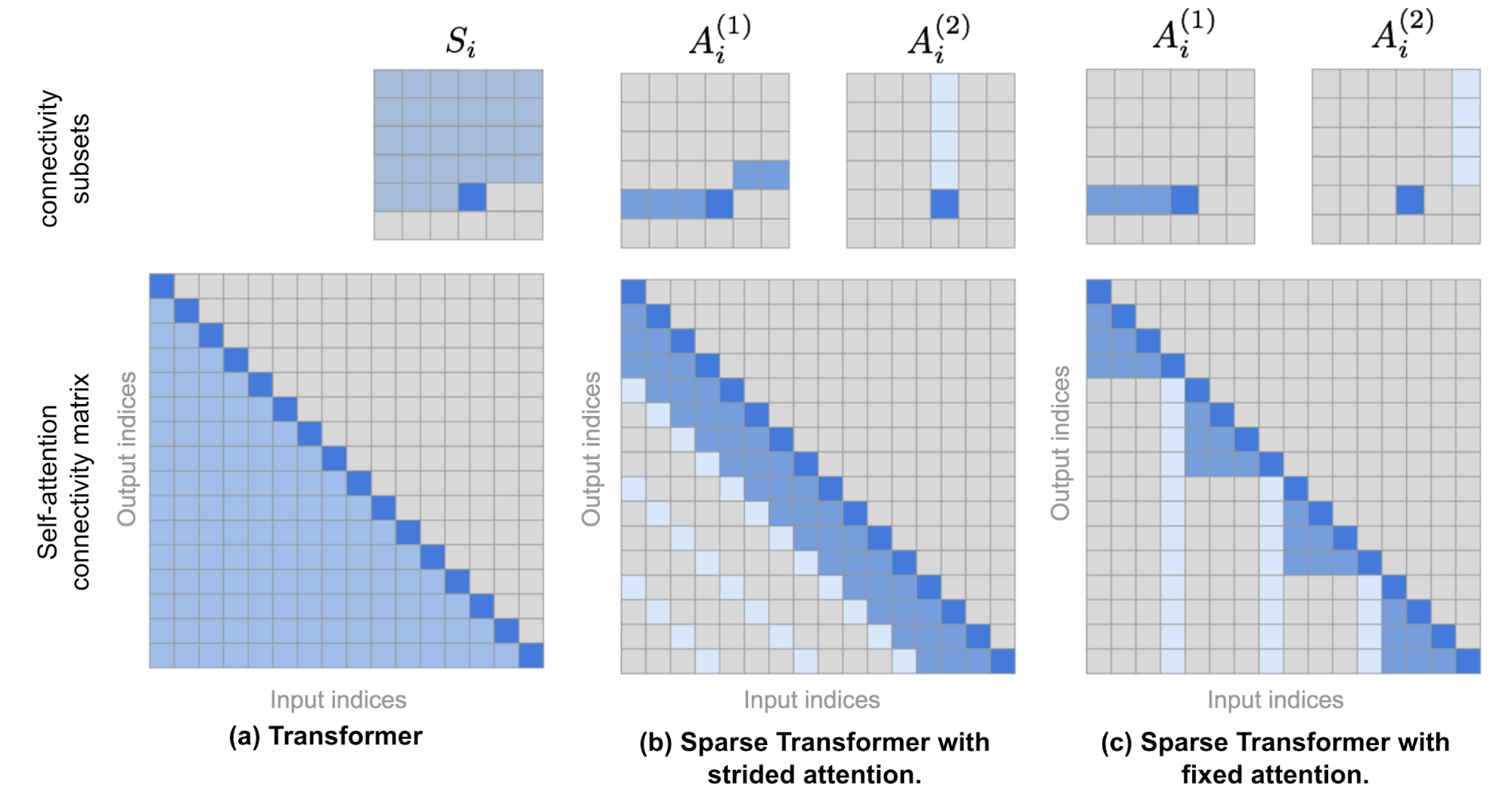
-
Strided attention with stride $\ell \sim \sqrt{n}$. This works well with image data as the structure is aligned with strides. In the image case, each pixel would attend to all the previous $\ell$ pixels in the raster scanning order (naturally cover the entire width of the image) and then those pixels attend to others in the same column (defined by another attention connectivity subset).
$$ \begin{aligned} A_i^{(1)} &= \{ t, t+1, \dots, i\} \text{, where } t = \max(0, i - \ell) \\ A_i^{(2)} &= \{j: (i-j) \mod \ell = 0\} \end{aligned} $$
-
Fixed attention. A small set of tokens summarize previous locations and propagate that information to all future locations.
$$ \begin{aligned} A_i^{(1)} &= \{j: \lfloor \frac{j}{\ell} \rfloor = \lfloor \frac{i}{\ell} \rfloor \} \\ A_i^{(2)} &= \{j: j \mod \ell \in \{\ell-c, \dots, \ell-1\} \} \end{aligned} $$where $c$ is a hyperparameter. If $c=1$, it restricts the representation whereas many depend on a few positions. The paper chose $c\in \{ 8, 16, 32 \}$ for $\ell \in \{ 128, 256 \}$.
Use Factorized Self-Attention in Transformer
There are three ways to use sparse factorized attention patterns in Transformer architecture:
- One attention type per residual block and then interleave them,
$\text{attn}(\mathbf{X}) = \text{Attend}(\mathbf{X}, A^{(n \mod p)}) \mathbf{W}^o$, where $n$ is the index of the current residual block. - Set up a single head which attends to locations that all the factorized heads attend to,
$\text{attn}(\mathbf{X}) = \text{Attend}(\mathbf{X}, \cup_{m=1}^p A^{(m)}) \mathbf{W}^o $. - Use a multi-head attention mechanism, but different from vanilla Transformer, each head might adopt a pattern presented above, 1 or 2. $\rightarrow$ This option often performs the best.
Sparse Transformer also proposed a set of changes so as to train the Transformer up to hundreds of layers, including gradient checkpointing, recomputing attention & FF layers during the backward pass, mixed precision training, efficient block-sparse implementation, etc. Please check the paper for more details or my previous post on techniques for scaling up model training.
Blockwise Attention (Qiu et al. 2019) introduces a sparse block matrix to only allow each token to attend to a small set of other tokens. Each attention matrix of size $L \times L$ is partitioned into $n \times n$ smaller blocks of size $\frac{L}{n}\times\frac{L}{n}$ and a sparse block matrix $\mathbf{M} \in \{0, 1\}^{L \times L}$ is defined by a permutation $\pi$ of ${1, \dots, n}$, which records the column index per row in the block matrix.
The actual implementation of Blockwise Attention only stores QKV as block matrices, each of size $n\times n$:
where $\hat{\mathbf{q}}_i$, $\hat{\mathbf{k}}_i$ and $\hat{\mathbf{v}}_i$ are the $i$-the row in the QKV block matrix respectively. Each $\mathbf{q}_i\mathbf{k}_{\pi(i)}^\top, \forall i = 1, \dots, n$ is of size $\frac{N}{n}\times\frac{N}{n}$ and therefore Blockwise Attention is able to reduce the memory complexity of attention matrix from $\mathcal{O}(L^2)$ to $\mathcal{O}(\frac{L}{n}\times\frac{L}{n} \times n) = \mathcal{O}(L^2/n)$.
Combination of Local and Global Context
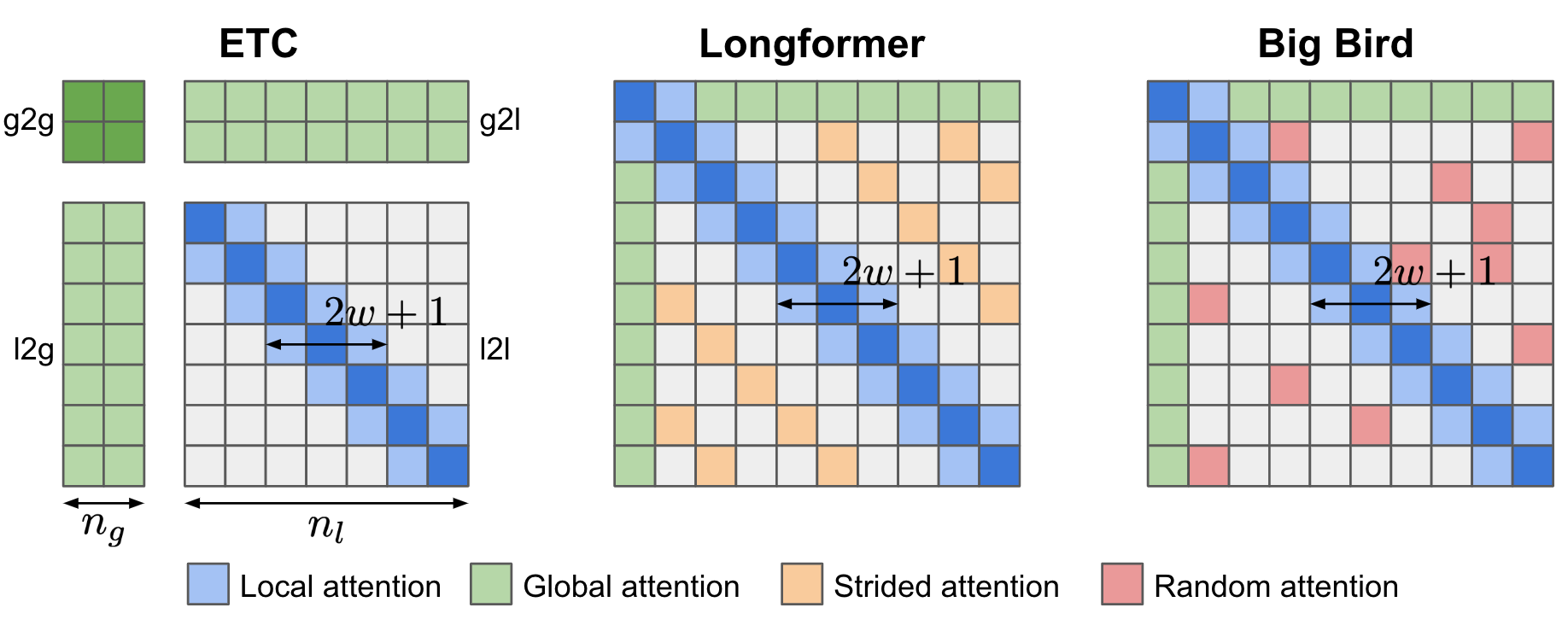
ETC (Extended Transformer Construction; Ainslie et al. 2019), Longformer (Beltagy et al. 2020) and Big Bird (Zaheer et al. 2020) models combine both local and global context when building an attention matrix. All these models can be initialized from existing pretrained models.
Global-Local Attention of ETC (Ainslie et al. 2019) takes two inputs, (1) the long input $\mathbf{x}^l$ of size $n_l$ which is the regular input sequence and (2) the global input $\mathbf{x}^g$ of size $n_g$ which contains a smaller number of auxiliary tokens, $n_g \ll n_l$. Attention is thus split into four components based on directional attention across these two inputs: g2g, g2l, l2g and l2l. Because the l2l attention piece can be very large, it is restricted to a fixed size attention span of radius $w$ (i.e. local attention span) and the l2l matrix can be reshaped to $n_l \times (2w+1)$.
ETC utilizes four binary matrices to handle structured inputs, $\mathbf{M}^{g2g}$, $\mathbf{M}^{g2l}$, $\mathbf{M}^{l2g}$ and $\mathbf{M}^{l2l}$. For example, each element $z^g_i \in \mathbb{R}^d$ in the attention output $z^g = (z^g_1, \dots, z^g_{n_g})$ for g2g attention piece is formatted as:
where $P^K_{ij}$ is a learnable vector for relative position encoding and $C$ is a very large constant ($C=10000$ in the paper) to offset any attention weights when mask is off.
One more update in ETC is to incorporate a CPC (contrastive predictive coding) task using NCE loss into the pretraining stage, besides the MLM task: The representation of one sentence should be similar to the representation of context around it when this sentence is masked.
The global input $\mathbf{x}^g$ for ETC is constructed as follows: Assuming there are some segments within the long inputs (e.g. by sentence), each segment is attached with one auxiliary token to learn global inputs. Relative position encoding is used to mark the global segment tokens with the token position. Hard masking in one direction (i.e., tokens before vs after are labeled differently) is found to bring performance gains in some datasets.
Attention pattern in Longformer contains three components:
- Local attention: Similar to ETC, local attention is controlled by a sliding window of fixed size $w$;
- Global attention of preselected tokens: Longformer has a few pre-selected tokens (e.g.
[CLS]token) assigned with global attention span, that is, attending to all other tokens in the input sequence. - Dilated attention: Dilated sliding window of fixed size $r$ and gaps of dilation size $d$, similar to Sparse Transformer;
Big Bird is quite similar to Longformer, equipped with both local attention and a few preselected tokens with global attention span, but Big Bird replaces dilated attention with a new mechanism where all tokens attend to a set of random tokens. The design is motivated by the fact that attention pattern can be viewed as a directed graph and a random graph has the property that information is able to rapidly flow between any pair of nodes.
Longformer uses smaller window size at lower layers and larger window sizes at higher layers. Ablation studies showed that this setup works better than reversed or fixed size config. Lower layers do not have dilated sliding windows to better learn to use immediate local context. Longformer also has a staged training procedure where initially the model is trained with small window size to learn from local context and then subsequent stages of training have window sizes increased and learning rate decreased.
Content-based Attention
The improvements proposed by Reformer (Kitaev, et al. 2020) aim to solve the following pain points in vanilla Transformer:
- Quadratic time and memory complexity within self-attention module.
- Memory in a model with $N$ layers is $N$-times larger than in a single-layer model because we need to store activations for back-propagation.
- The intermediate FF layers are often quite large.
Reformer proposed two main changes:
- Replace the dot-product attention with locality-sensitive hashing (LSH) attention, reducing the complexity from $\mathcal{O}(L^2)$ to $\mathcal{O}(L\log L)$.
- Replace the standard residual blocks with reversible residual layers, which allows storing activations only once during training instead of $N$ times (i.e. proportional to the number of layers).
Locality-Sensitive Hashing Attention
In $\mathbf{Q} \mathbf{K}^\top$ part of the attention formula, we are only interested in the largest elements as only large elements contribute a lot after softmax. For each query $\mathbf{q}_i \in \mathbf{Q}$, we are looking for row vectors in $\mathbf{K}$ closest to $\mathbf{q}_i$. In order to find nearest neighbors quickly in high-dimensional space, Reformer incorporates Locality-Sensitive Hashing (LSH) into its attention mechanism.
A hashing scheme $x \mapsto h(x)$ is locality-sensitive if it preserves the distancing information between data points, such that close vectors obtain similar hashes while distant vectors have very different ones. The Reformer adopts a hashing scheme as such, given a fixed random matrix $\mathbf{R} \in \mathbb{R}^{d \times b/2}$ (where $b$ is a hyperparam), the hash function is $h(x) = \arg\max([xR; −xR])$.
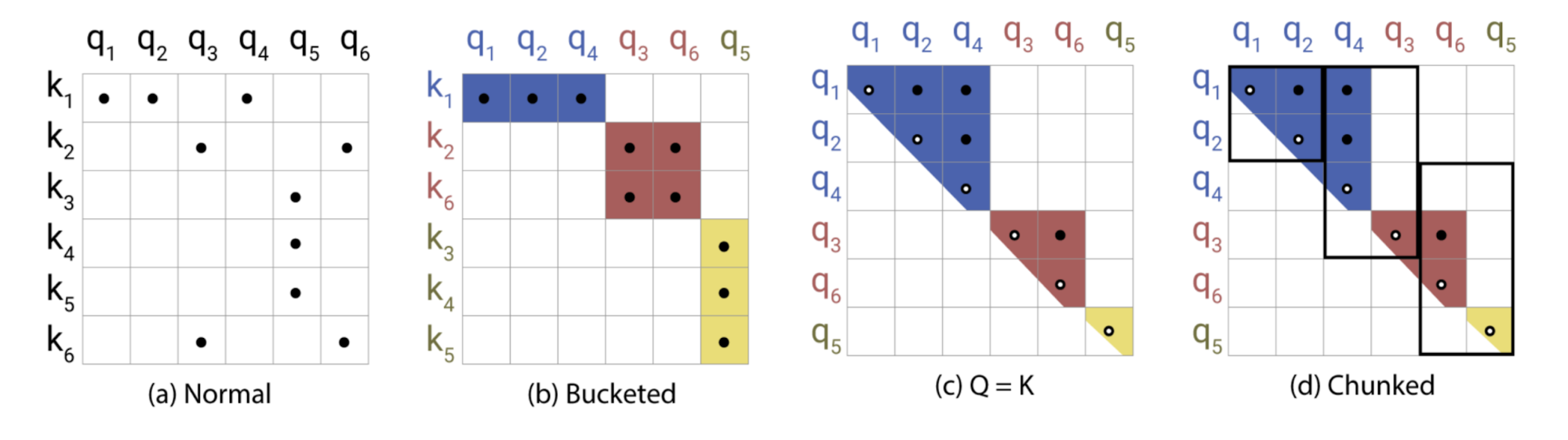
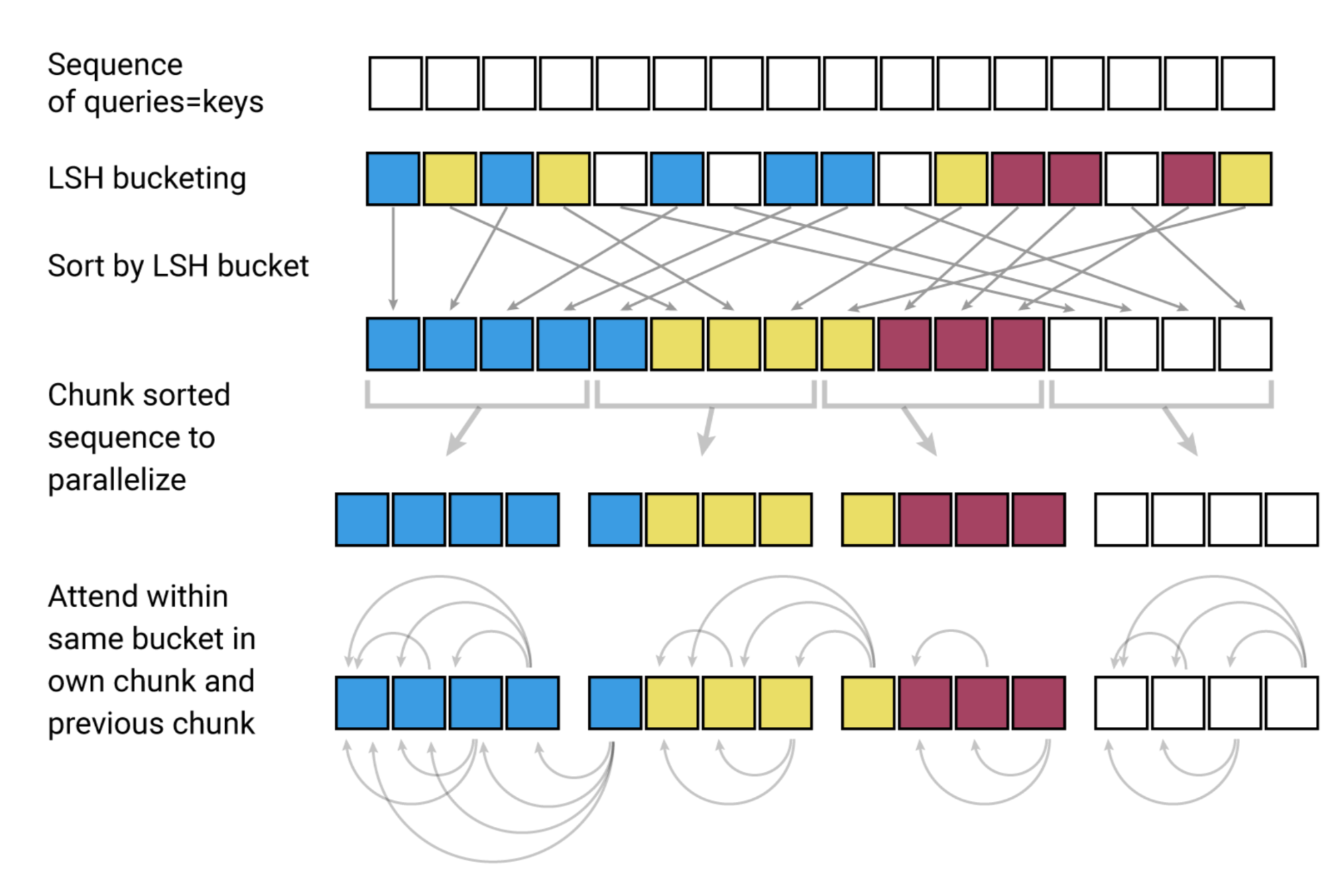
In LSH attention, a query can only attend to positions in the same hashing bucket, $S_i = \{j: h(\mathbf{q}_i) = h(\mathbf{k}_j)\}$. It is carried out in the following process, as illustrated in Fig. 20:
- (a) The attention matrix for full attention is often sparse.
- (b) Using LSH, we can sort the keys and queries to be aligned according to their hash buckets.
- (c) Set $\mathbf{Q} = \mathbf{K}$ (precisely $\mathbf{k}_j = \mathbf{q}_j / |\mathbf{q}_j|$), so that there are equal numbers of keys and queries in one bucket, easier for batching. Interestingly, this “shared-QK” config does not affect the performance of the Transformer.
- (d) Apply batching where chunks of $m$ consecutive queries are grouped together.
Reversible Residual Network
Another improvement by Reformer is to use reversible residual layers (Gomez et al. 2017). The motivation for reversible residual network is to design the architecture in a way that activations at any given layer can be recovered from the activations at the following layer, using only the model parameters. Hence, we can save memory by recomputing the activation during backprop rather than storing all the activations.
Given a layer $x \mapsto y$, the normal residual layer does $y = x + F(x)$, but the reversible layer splits both input and output into pairs $(x_1, x_2) \mapsto (y_1, y_2)$ and then executes the following:
and reversing is easy:
Reformer applies the same idea to Transformer by combination attention ($F$) and feed-forward layers ($G$) within a reversible net block:
The memory can be further reduced by chunking the feed-forward computation:
The resulting reversible Transformer does not need to store activation in every layer.
Routing Transformer (Roy et al. 2021) is also built on content-based clustering of keys and queries. Instead of using a static hashing function like LSH, it utilizes online $k$-means clustering and combines it with local, temporal sparse attention to reduce the attention complexity from $O(L^2)$ to $O(L^{1.5})$.
Within routing attention, both keys and queries are clustered with $k$-means clustering method and the same set of centroids $\boldsymbol{\mu} = (\mu_1, \dots, \mu_k) \in \mathbb{R}^{k \times d}$. Queries are routed to keys that get assigned to the same centroid. The total complexity is $O(Lkd + L^2d/k)$, where $O(Lkd)$ is for running clustering assignments and $O(L^2d/k)$ is for attention computation. The cluster centroids are updated by EMA (exponential moving average) using all associated keys and queries.
In the experiments for Routing Transformer, some best config only has routing attention enabled in the last two layers of the model and half of the attention heads, while the other half utilizing local attention. They also observed that local attention is a pretty strong baseline and larger attention window always leads to better results.
Low-Rank Attention
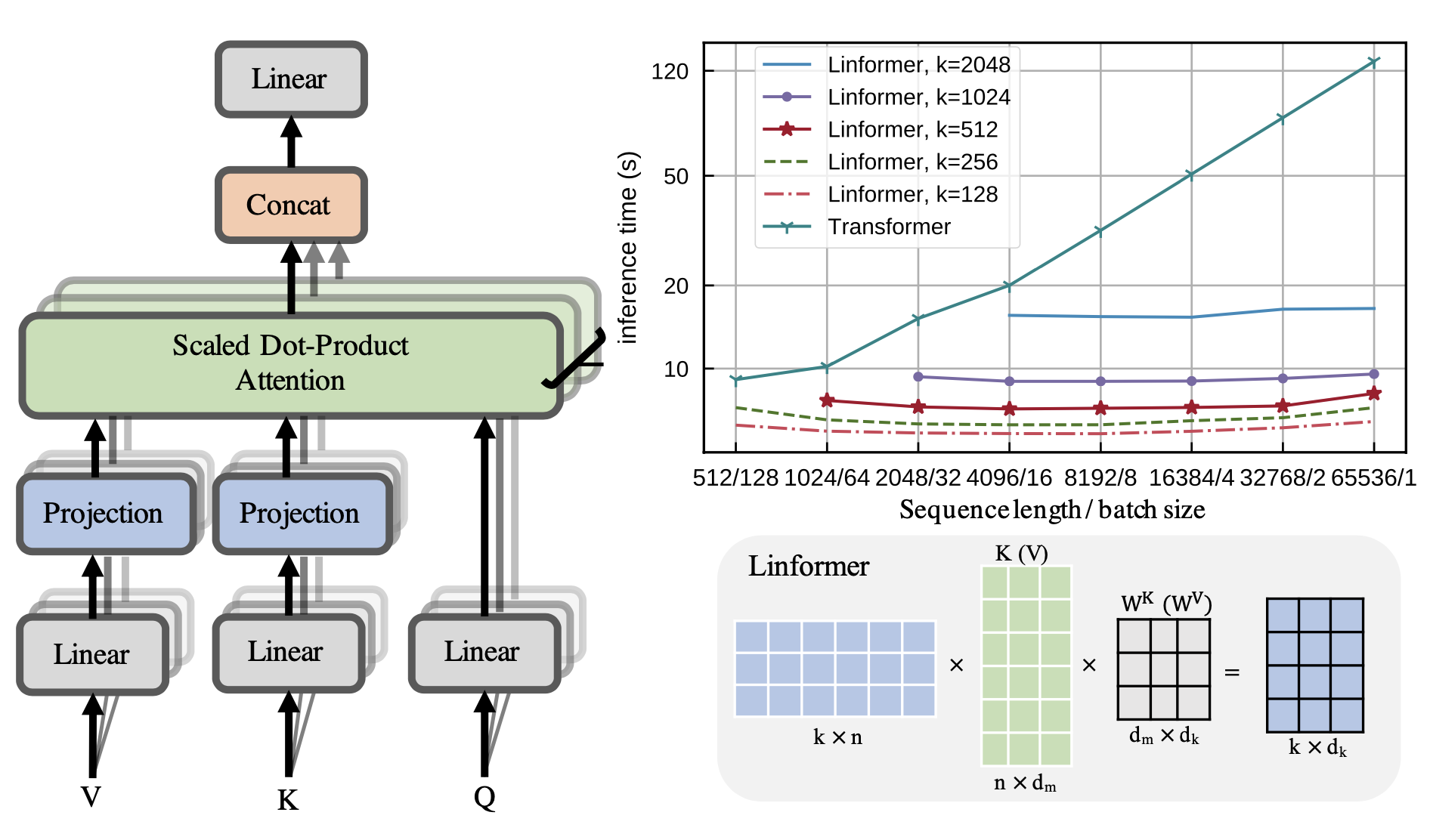
Linformer (Wang et al. 2020) approximates the full attention matrix with a low rank matrix, reducing the time & space complexity to be linear. Instead of using expensive SVD to identify low rank decomposition, Linformer adds two linear projections $\mathbf{E}_i, \mathbf{F}_i \in \mathbb{R}^{L \times k}$ for key and value matrices, respectively, reducing their dimensions from $L \times d$ to $k \times d$. As long as $k \ll L$, the attention memory can be greatly reduced.
Additional techniques can be applied to further improve efficiency of Linformer:
- Parameter sharing between projection layers, such as head-wise, key-value and layer-wise (across all layers) sharing.
- Use different $k$ at different layers, as heads in higher layers tend to have a more skewed distribution (lower rank) and thus we can use smaller $k$ at higher layers.
- Use different types of projections; e.g. mean/max pooling, convolution layer with kernel and stride $L/k$.
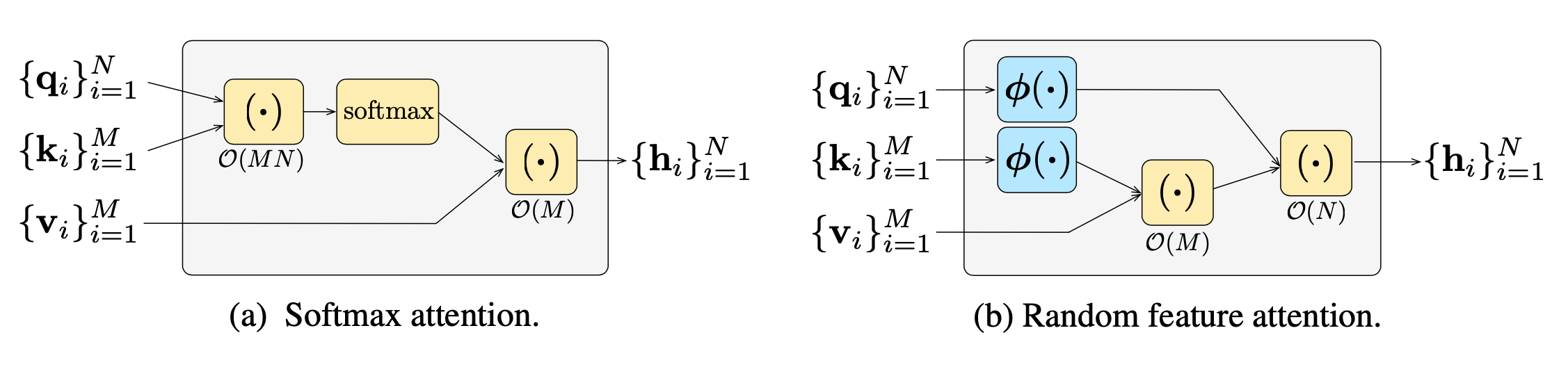
Random Feature Attention (RFA; Peng et al. 2021) relies on random feature methods (Rahimi & Recht, 2007) to approximate softmax operation in self-attention with low rank feature maps in order to achieve linear time and space complexity. Performers (Choromanski et al. 2021) also adopts random feature attention with improvements on the kernel construction to further reduce the kernel approximation error.
The main theorem behind RFA is from Rahimi & Recht, 2007:
Let $\phi: \mathbb{R}^d \to \mathbb{R}^{2D}$ be a nonlinear transformation:
$$ \phi(\mathbf{x}) = \frac{1}{\sqrt{D}}[\sin(\mathbf{w}_1^\top \mathbf{x}), \dots, \sin(\mathbf{w}_D^\top \mathbf{x}), \cos(\mathbf{w}_1^\top \mathbf{x}), \dots, \cos(\mathbf{w}_D^\top \mathbf{x})]^\top $$When $d$-dimensional random vectors $\mathbf{w}_i$ are i.i.d. from $\mathcal{N}(\mathbf{0}, \sigma^2\mathbf{I}_d)$, $$ \mathbb{E}_{\mathbf{w}_i} [\phi(\mathbf{x}) \cdot \phi(\mathbf{y})] = \exp(-\frac{\| \mathbf{x} - \mathbf{y} \|^2}{2\sigma^2}) $$
An unbiased estimation of $\exp(\mathbf{x} \cdot \mathbf{y})$ is:
Then we can write the attention function as follows, where $\otimes$ is outer product operation and $\sigma^2$ is the temperature:
Causal Attention RFA has token at time step $t$ only attend to earlier keys and values $\{\mathbf{k}_i\}_{i \leq t}, \{\mathbf{v}_i\}_{i \leq t}$. Let us use a tuple of variables, $(\mathbf{S}_t \in \mathbb{R}^{2D \times d}, \mathbf{z} \in \mathbb{R}^{2D})$, to track the hidden state history at time step $t$, similar to RNNs:
where $2D$ is the size of $\phi(.)$ and $D$ should be no less than the model size $d$ for reasonable approximation.
RFA leads to significant speedup in autoregressive decoding and the memory complexity mainly depends on the choice of $D$ when constructing the kernel $\phi(.)$.
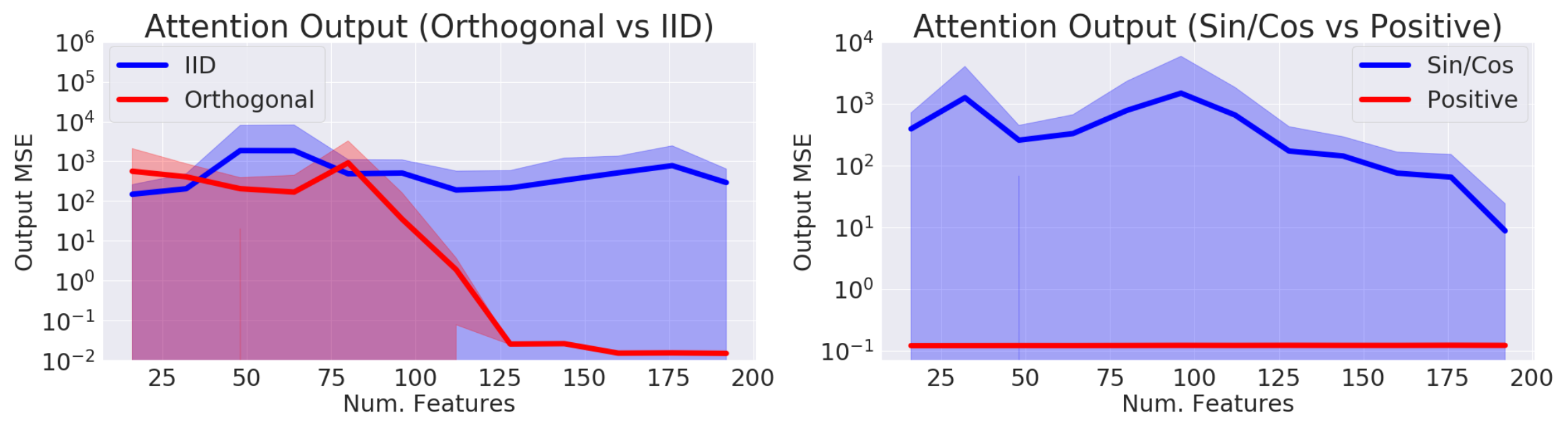
Performer modifies the random feature attention with positive random feature maps to reduce the estimation error. It also keeps the randomly sampled $\mathbf{w}_1, \dots, \mathbf{w}_D$ to be orthogonal to further reduce the variance of the estimator.
Transformers for Reinforcement Learning
The self-attention mechanism avoids compressing the whole past into a fixed-size hidden state and does not suffer from vanishing or exploding gradients as much as RNNs. Reinforcement Learning tasks can for sure benefit from these traits. However, it is quite difficult to train Transformer even in supervised learning, let alone in the RL context. It could be quite challenging to stabilize and train a LSTM agent by itself, after all.
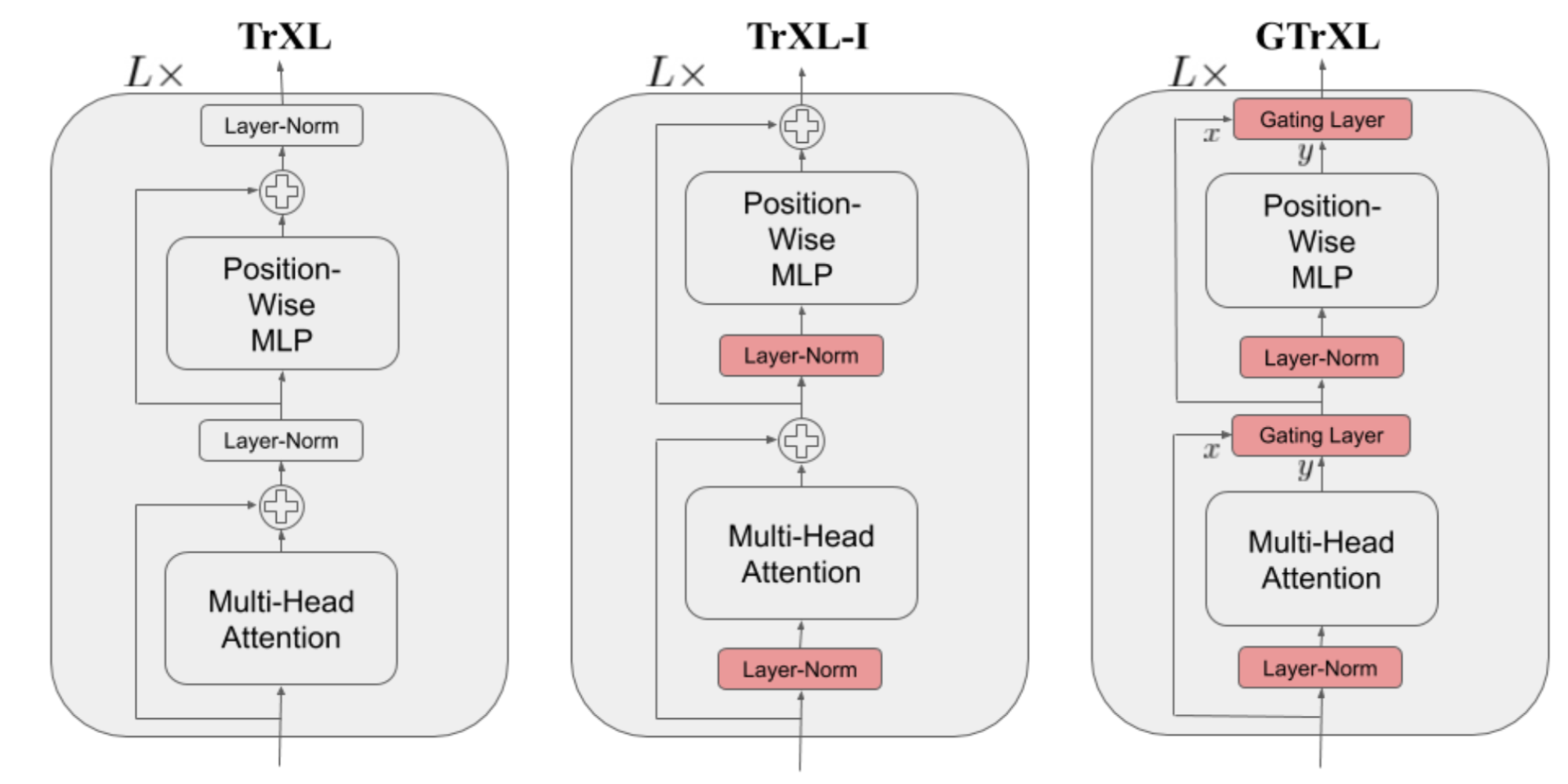
The Gated Transformer-XL (GTrXL; Parisotto, et al. 2019) is one attempt to use Transformer for RL. GTrXL succeeded in stabilizing training with two changes on top of Transformer-XL:
- The layer normalization is only applied on the input stream in a residual module, but NOT on the shortcut stream. A key benefit to this reordering is to allow the original input to flow from the first to last layer.
- The residual connection is replaced with a GRU-style (Gated Recurrent Unit; Chung et al., 2014) gating mechanism.
The gating function parameters are explicitly initialized to be close to an identity map - this is why there is a $b_g$ term. A $b_g > 0$ greatly helps with the learning speedup.
Decision Transformer (DT; Chen et al 2021) formulates Reinforcement Learning problems as a process of conditional sequence modeling, outputting the optimal actions conditioned on the desired return, past states and actions. It therefore becomes straightforward to use Transformer architecture. Decision Transformer is for off-policy RL, where the model only has access to a fixed collection of trajectories collected by other policies.
To encourage the model to learn how to act in order to achieve a desired return, it feeds the model with desired future return $\hat{R} = \sum_{t’=t}^T r_{t’}$ instead of the current reward. The trajectory consists of a list of triplets, (return-to-go $\hat{R}_t, state $s_t$, action $a_t$), and it is used as an input sequence for Transformer:
Three linear layers are added and trained for return-to-go, state and action respectively to extract token embeddings. The prediction head learns to predict $a_t$ corresponding to the input token $s_t$. The training uses cross-entropy loss for discrete actions or MSE for continuous actions. Predicting the states or return-to-go was not found to help improve the performance in their experiments.
The experiments compared DT with several model-free RL algorithm baselines and showed that:
- DT is more efficient than behavior cloning in low data regime;
- DT can model the distribution of returns very well;
- Having a long context is crucial for obtaining good results;
- DT can work with sparse rewards.
Citation
Cited as:
Weng, Lilian. (Jan 2023). The transformer family version 2.0. Lil’Log. https://lilianweng.github.io/posts/2023-01-27-the-transformer-family-v2/.
Or
@article{weng2023transformer,
title = "The Transformer Family Version 2.0",
author = "Weng, Lilian",
journal = "lilianweng.github.io",
year = "2023",
month = "Jan",
url = "https://lilianweng.github.io/posts/2023-01-27-the-transformer-family-v2/"
}
References
[1] Ashish Vaswani, et al. “Attention is all you need.” NIPS 2017.
[2] Rami Al-Rfou, et al. “Character-level language modeling with deeper self-attention.” AAAI 2019.
[3] Olah & Carter, “Attention and Augmented Recurrent Neural Networks”, Distill, 2016.
[4] Sainbayar Sukhbaatar, et al. “Adaptive Attention Span in Transformers”. ACL 2019.
[5] Rewon Child, et al. “Generating Long Sequences with Sparse Transformers” arXiv:1904.10509 (2019).
[6] Nikita Kitaev, et al. “Reformer: The Efficient Transformer” ICLR 2020.
[7] Alex Graves. (“Adaptive Computation Time for Recurrent Neural Networks”)[https://arxiv.org/abs/1603.08983]
[8] Niki Parmar, et al. “Image Transformer” ICML 2018.
[9] Zihang Dai, et al. “Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context.” ACL 2019.
[10] Aidan N. Gomez, et al. “The Reversible Residual Network: Backpropagation Without Storing Activations” NIPS 2017.
[11] Mostafa Dehghani, et al. “Universal Transformers” ICLR 2019.
[12] Emilio Parisotto, et al. “Stabilizing Transformers for Reinforcement Learning” arXiv:1910.06764 (2019).
[13] Rae et al. “Compressive Transformers for Long-Range Sequence Modelling.” 2019.
[14] Press et al. “Train Short, Test Long: Attention With Linear Biases Enables Input Length Extrapolation.” ICLR 2022.
[15] Wu, et al. “DA-Transformer: Distance Aware Transformer” 2021.
[16] Elabyad et al. “Depth-Adaptive Transformer.” ICLR 2020.
[17] Schuster et al. “Confident Adaptive Language Modeling” 2022.
[18] Qiu et al. “Blockwise self-attention for long document understanding” 2019
[19] Roy et al. “Efficient Content-Based Sparse Attention with Routing Transformers.” 2021.
[20] Ainslie et al. “ETC: Encoding Long and Structured Inputs in Transformers.” EMNLP 2019.
[21] Beltagy et al. “Longformer: The long-document transformer.” 2020.
[22] Zaheer et al. “Big Bird: Transformers for Longer Sequences.” 2020.
[23] Wang et al. “Linformer: Self-Attention with Linear Complexity.” arXiv preprint arXiv:2006.04768 (2020).
[24] Tay et al. 2020 “Sparse Sinkhorn Attention.” ICML 2020.
[25] Peng et al. “Random Feature Attention.” ICLR 2021.
[26] Choromanski et al. “Rethinking Attention with Performers.” ICLR 2021.
[27] Khandelwal et al. “Generalization through memorization: Nearest neighbor language models.” ICLR 2020.
[28] Yogatama et al. “Adaptive semiparametric language models.” ACL 2021.
[29] Wu et al. “Memorizing Transformers.” ICLR 2022.
[30] Su et al. “Roformer: Enhanced transformer with rotary position embedding.” arXiv preprint arXiv:2104.09864 (2021).
[31] Shaw et al. “Self-attention with relative position representations.” arXiv preprint arXiv:1803.02155 (2018).
[32] Tay et al. “Efficient Transformers: A Survey.” ACM Computing Surveys 55.6 (2022): 1-28.
[33] Chen et al., “Decision Transformer: Reinforcement Learning via Sequence Modeling” arXiv preprint arXiv:2106.01345 (2021).