When facing a limited amount of labeled data for supervised learning tasks, four approaches are commonly discussed.
- Pre-training + fine-tuning: Pre-train a powerful task-agnostic model on a large unsupervised data corpus, e.g. pre-training LMs on free text, or pre-training vision models on unlabelled images via self-supervised learning, and then fine-tune it on the downstream task with a small set of labeled samples.
- Semi-supervised learning: Learn from the labelled and unlabeled samples together. A lot of research has happened on vision tasks within this approach.
- Active learning: Labeling is expensive, but we still want to collect more given a cost budget. Active learning learns to select most valuable unlabeled samples to be collected next and helps us act smartly with a limited budget.
- Pre-training + dataset auto-generation: Given a capable pre-trained model, we can utilize it to auto-generate a lot more labeled samples. This has been especially popular within the language domain driven by the success of few-shot learning.
I plan to write a series of posts on the topic of “Learning with not enough data”. Part 1 is on Semi-Supervised Learning.
What is semi-supervised learning?
Semi-supervised learning uses both labeled and unlabeled data to train a model.
Interestingly most existing literature on semi-supervised learning focuses on vision tasks. And instead pre-training + fine-tuning is a more common paradigm for language tasks.
All the methods introduced in this post have a loss combining two parts: $\mathcal{L} = \mathcal{L}_s + \mu(t) \mathcal{L}_u$. The supervised loss $\mathcal{L}_s$ is easy to get given all the labeled examples. We will focus on how the unsupervised loss $\mathcal{L}_u$ is designed. A common choice of the weighting term $\mu(t)$ is a ramp function increasing the importance of $\mathcal{L}_u$ in time, where $t$ is the training step.
Disclaimer: The post is not gonna cover semi-supervised methods with focus on model architecture modification. Check this survey for how to use generative models and graph-based methods in semi-supervised learning.
Notations
| Symbol | Meaning |
|---|---|
| $L$ | Number of unique labels. |
| $(\mathbf{x}^l, y) \sim \mathcal{X}, y \in \{0, 1\}^L$ | Labeled dataset. $y$ is a one-hot representation of the true label. |
| $\mathbf{u} \sim \mathcal{U}$ | Unlabeled dataset. |
| $\mathcal{D} = \mathcal{X} \cup \mathcal{U}$ | The entire dataset, including both labeled and unlabeled examples. |
| $\mathbf{x}$ | Any sample which can be either labeled or unlabeled. |
| $\bar{\mathbf{x}}$ | $\mathbf{x}$ with augmentation applied. |
| $\mathbf{x}_i$ | The $i$-th sample. |
| $\mathcal{L}$, $\mathcal{L}_s$, $\mathcal{L}_u$ | Loss, supervised loss, and unsupervised loss. |
| $\mu(t)$ | The unsupervised loss weight, increasing in time. |
| $p(y \vert \mathbf{x}), p_\theta(y \vert \mathbf{x})$ | The conditional probability over the label set given the input. |
| $f_\theta(.)$ | The implemented neural network with weights $\theta$, the model that we want to train. |
| $\mathbf{z} = f_\theta(\mathbf{x})$ | A vector of logits output by $f$. |
| $\hat{y} = \text{softmax}(\mathbf{z})$ | The predicted label distribution. |
| $D[.,.]$ | A distance function between two distributions, such as MSE, cross entropy, KL divergence, etc. |
| $\beta$ | EMA weighting hyperparameter for teacher model weights. |
| $\alpha, \lambda$ | Parameters for MixUp, $\lambda \sim \text{Beta}(\alpha, \alpha)$. |
| $T$ | Temperature for sharpening the predicted distribution. |
| $\tau$ | A confidence threshold for selecting the qualified prediction. |
Hypotheses
Several hypotheses have been discussed in literature to support certain design decisions in semi-supervised learning methods.
-
H1: Smoothness Assumptions: If two data samples are close in a high-density region of the feature space, their labels should be the same or very similar.
-
H2: Cluster Assumptions: The feature space has both dense regions and sparse regions. Densely grouped data points naturally form a cluster. Samples in the same cluster are expected to have the same label. This is a small extension of H1.
-
H3: Low-density Separation Assumptions: The decision boundary between classes tends to be located in the sparse, low density regions, because otherwise the decision boundary would cut a high-density cluster into two classes, corresponding to two clusters, which invalidates H1 and H2.
-
H4: Manifold Assumptions: The high-dimensional data tends to locate on a low-dimensional manifold. Even though real-world data might be observed in very high dimensions (e.g. such as images of real-world objects/scenes), they actually can be captured by a lower dimensional manifold where certain attributes are captured and similar points are grouped closely (e.g. images of real-world objects/scenes are not drawn from a uniform distribution over all pixel combinations). This enables us to learn a more efficient representation for us to discover and measure similarity between unlabeled data points. This is also the foundation for representation learning. [see a helpful link].
Consistency Regularization
Consistency Regularization, also known as Consistency Training, assumes that randomness within the neural network (e.g. with Dropout) or data augmentation transformations should not modify model predictions given the same input. Every method in this section has a consistency regularization loss as $\mathcal{L}_u$.
This idea has been adopted in several self-supervised learning methods, such as SimCLR, BYOL, SimCSE, etc. Different augmented versions of the same sample should result in the same representation. Cross-view training in language modeling and multi-view learning in self-supervised learning all share the same motivation.
Π-model

Sajjadi et al. (2016) proposed an unsupervised learning loss to minimize the difference between two passes through the network with stochastic transformations (e.g. dropout, random max-pooling) for the same data point. The label is not explicitly used, so the loss can be applied to unlabeled dataset. Laine & Aila (2017) later coined the name, Π-Model, for such a setup.
where $f’$ is the same neural network with different stochastic augmentation or dropout masks applied. This loss utilizes the entire dataset.
Temporal ensembling
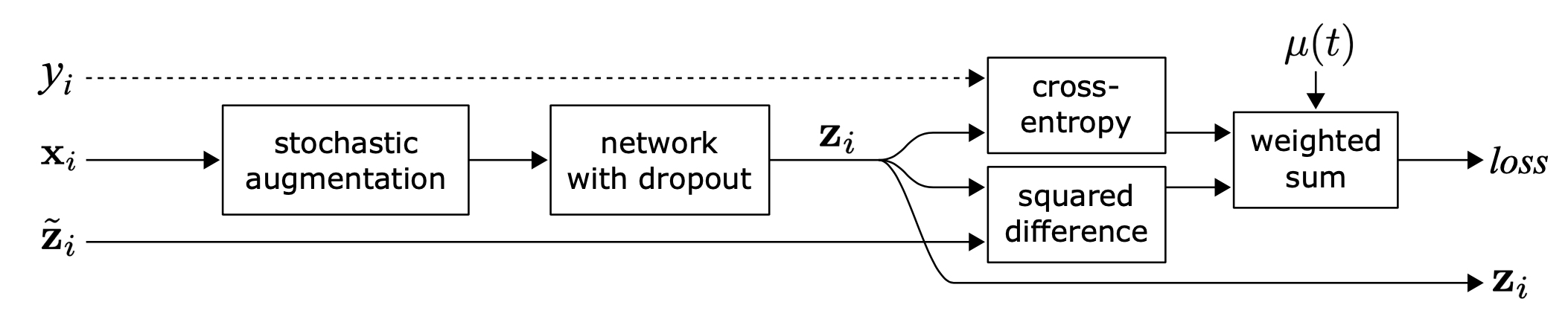
Π-model requests the network to run two passes per sample, doubling the computation cost. To reduce the cost, Temporal Ensembling (Laine & Aila 2017) maintains an exponential moving average (EMA) of the model prediction in time per training sample $\tilde{\mathbf{z}}_i$ as the learning target, which is only evaluated and updated once per epoch. Because the ensemble output $\tilde{\mathbf{z}}_i$ is initialized to $\mathbf{0}$, it is normalized by $(1-\alpha^t)$ to correct this startup bias. Adam optimizer has such bias correction terms for the same reason.
where $\tilde{\mathbf{z}}^{(t)}$ is the ensemble prediction at epoch $t$ and $\mathbf{z}_i$ is the model prediction in the current round. Note that since $\tilde{\mathbf{z}}^{(0)} = \mathbf{0}$, with correction, $\tilde{\mathbf{z}}^{(1)}$ is simply equivalent to $\mathbf{z}_i$ at epoch 1.
Mean teachers
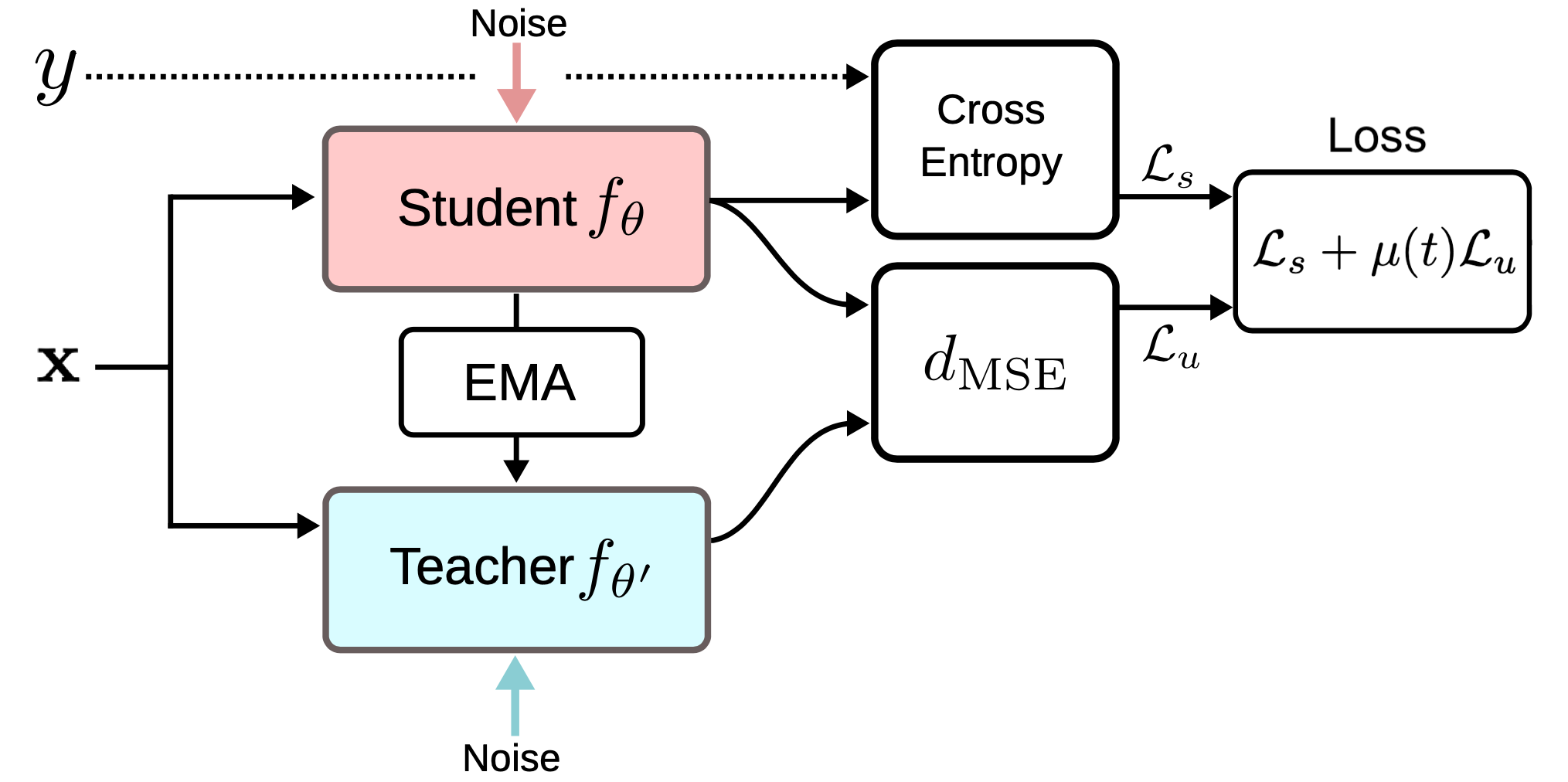
Temporal Ensembling keeps track of an EMA of label predictions for each training sample as a learning target. However, this label prediction only changes every epoch, making the approach clumsy when the training dataset is large. Mean Teacher (Tarvaninen & Valpola, 2017) is proposed to overcome the slowness of target update by tracking the moving average of model weights instead of model outputs. Let’s call the original model with weights $\theta$ as the student model and the model with moving averaged weights $\theta’$ across consecutive student models as the mean teacher: $\theta’ \gets \beta \theta’ + (1-\beta)\theta$
The consistency regularization loss is the distance between predictions by the student and teacher and the student-teacher gap should be minimized. The mean teacher is expected to provide more accurate predictions than the student. It got confirmed in the empirical experiments, as shown in 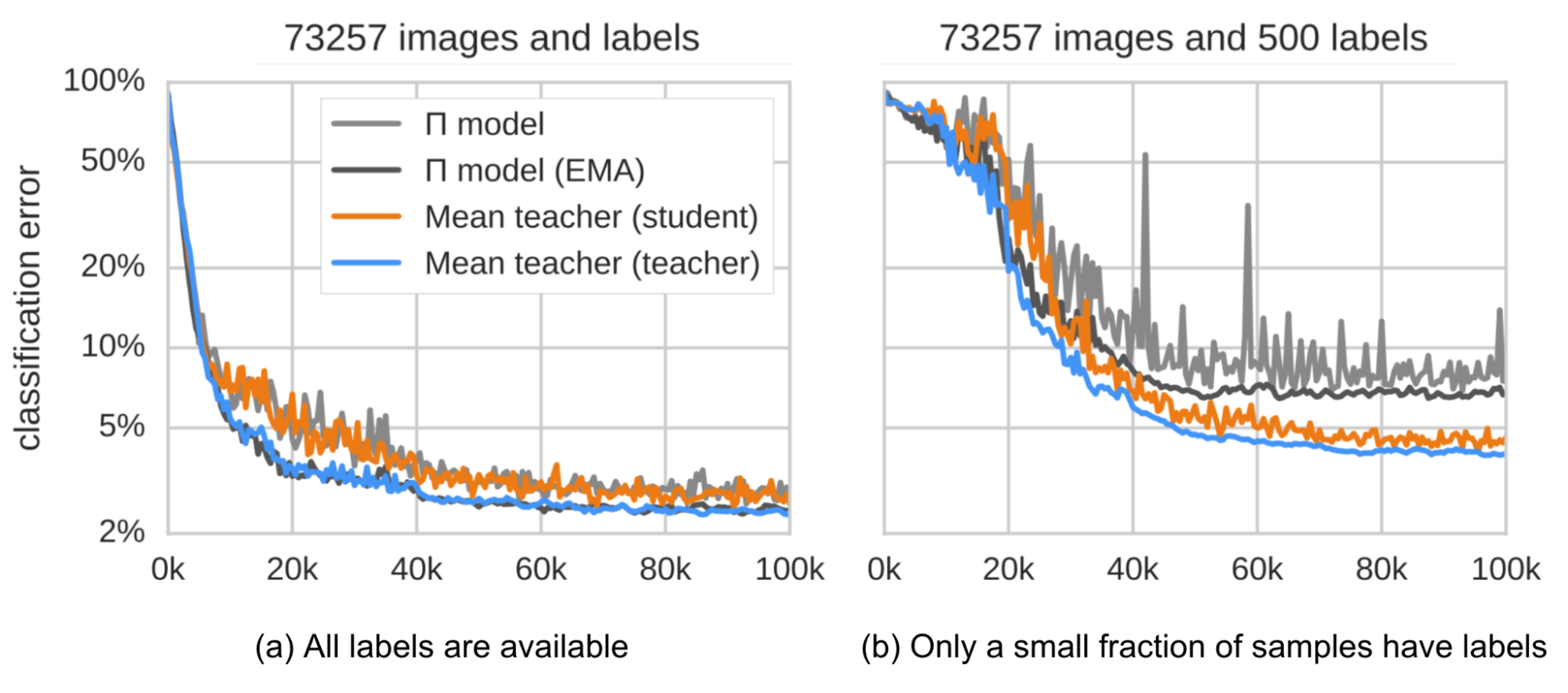
According to their ablation studies,
- Input augmentation (e.g. random flips of input images, Gaussian noise) or student model dropout is necessary for good performance. Dropout is not needed on the teacher model.
- The performance is sensitive to the EMA decay hyperparameter $\beta$. A good strategy is to use a small $\beta=0.99$ during the ramp up stage and a larger $\beta=0.999$ in the later stage when the student model improvement slows down.
- They found that MSE as the consistency cost function performs better than other cost functions like KL divergence.
Noisy samples as learning targets
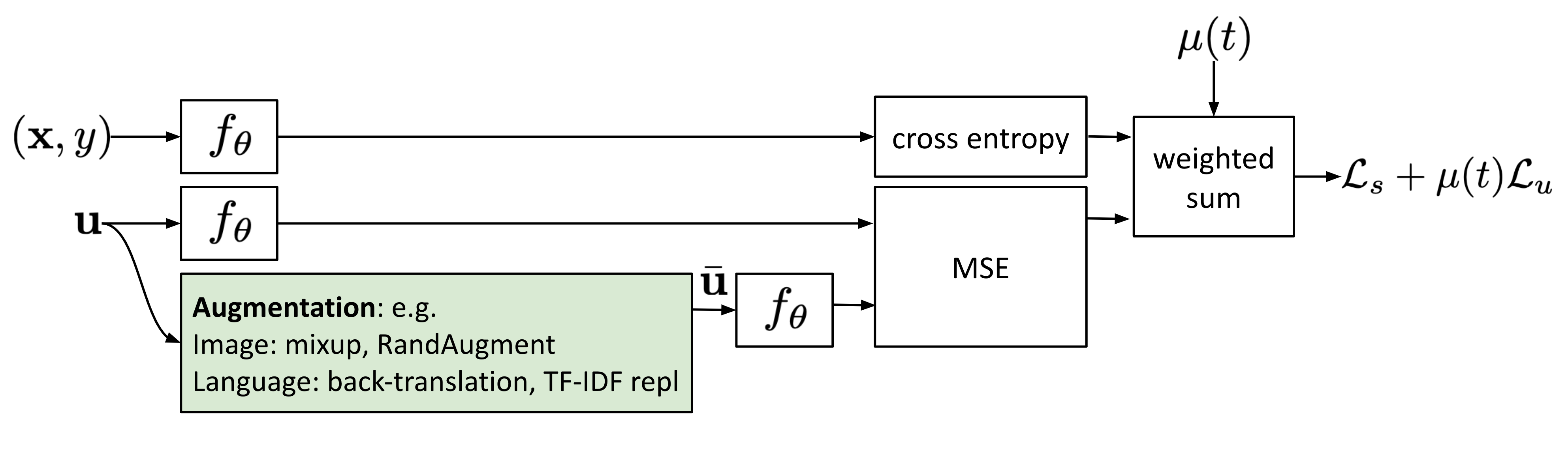
Several recent consistency training methods learn to minimize prediction difference between the original unlabeled sample and its corresponding augmented version. It is quite similar to the Π-model but the consistency regularization loss is only applied to the unlabeled data.
Adversarial Training (Goodfellow et al. 2014) applies adversarial noise onto the input and trains the model to be robust to such adversarial attack. The setup works in supervised learning,
where $q(y \mid \mathbf{x}^l)$ is the true distribution, approximated by one-hot encoding of the ground truth label, $y$. $p_\theta(y \mid \mathbf{x}^l)$ is the model prediction. $D[.,.]$ is a distance function measuring the divergence between two distributions.
Virtual Adversarial Training (VAT; Miyato et al. 2018) extends the idea to work in semi-supervised learning. Because $q(y \mid \mathbf{x}^l)$ is unknown, VAT replaces it with the current model prediction for the original input with the current weights $\hat{\theta}$. Note that $\hat{\theta}$ is a fixed copy of model weights, so there is no gradient update on $\hat{\theta}$.
The VAT loss applies to both labeled and unlabeled samples. It is a negative smoothness measure of the current model’s prediction manifold at each data point. The optimization of such loss motivates the manifold to be smoother.
Interpolation Consistency Training (ICT; Verma et al. 2019) enhances the dataset by adding more interpolations of data points and expects the model prediction to be consistent with interpolations of the corresponding labels. MixUp (Zheng et al. 2018) operation mixes two images via a simple weighted sum and combines it with label smoothing. Following the idea of MixUp, ICT expects the prediction model to produce a label on a mixup sample to match the interpolation of predictions of corresponding inputs:
where $\theta’$ is a moving average of $\theta$, which is a mean teacher.
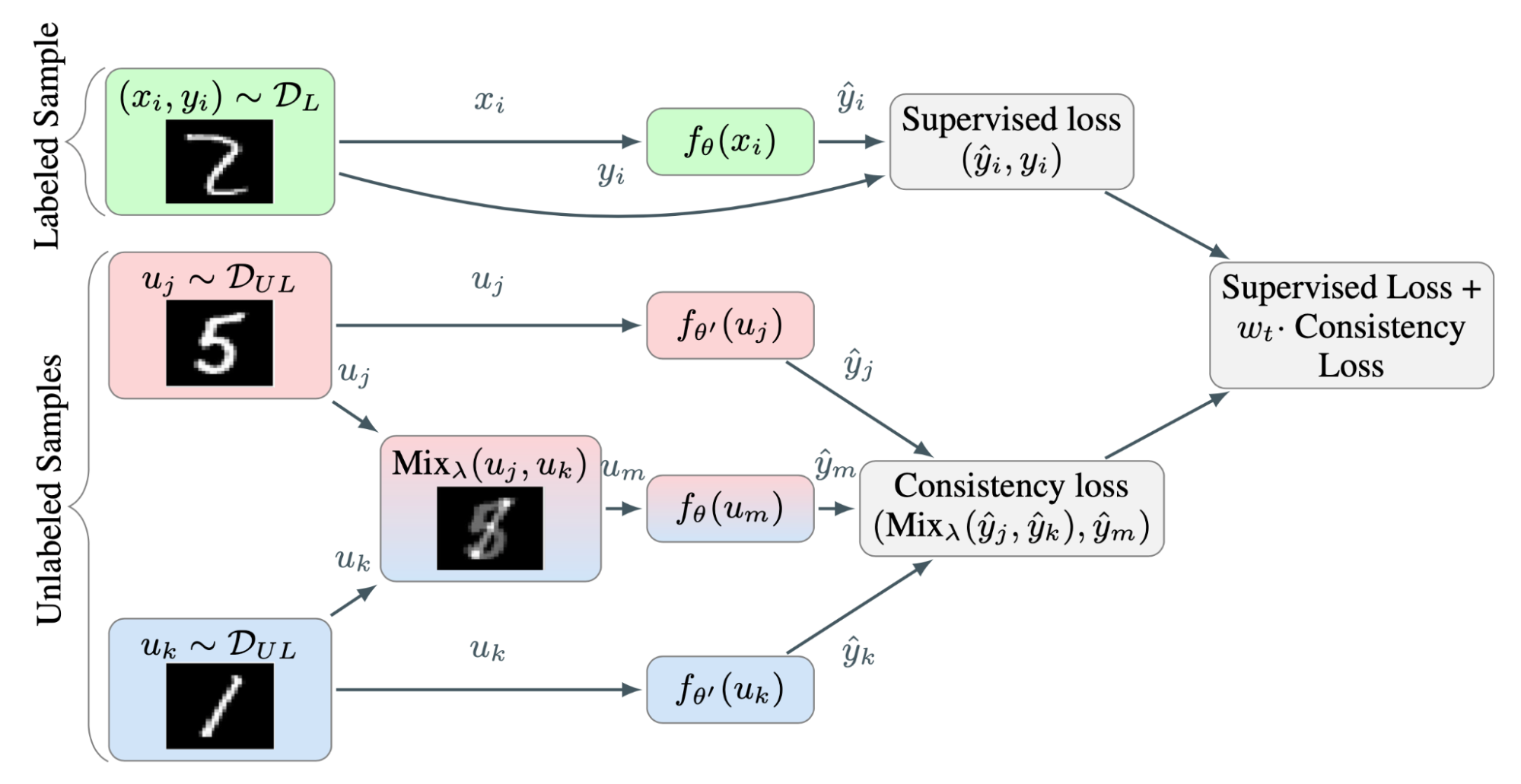
Because the probability of two randomly selected unlabeled samples belonging to different classes is high (e.g. There are 1000 object classes in ImageNet), the interpolation by applying a mixup between two random unlabeled samples is likely to happen around the decision boundary. According to the low-density separation assumptions, the decision boundary tends to locate in the low density regions.
where $\theta’$ is a moving average of $\theta$.
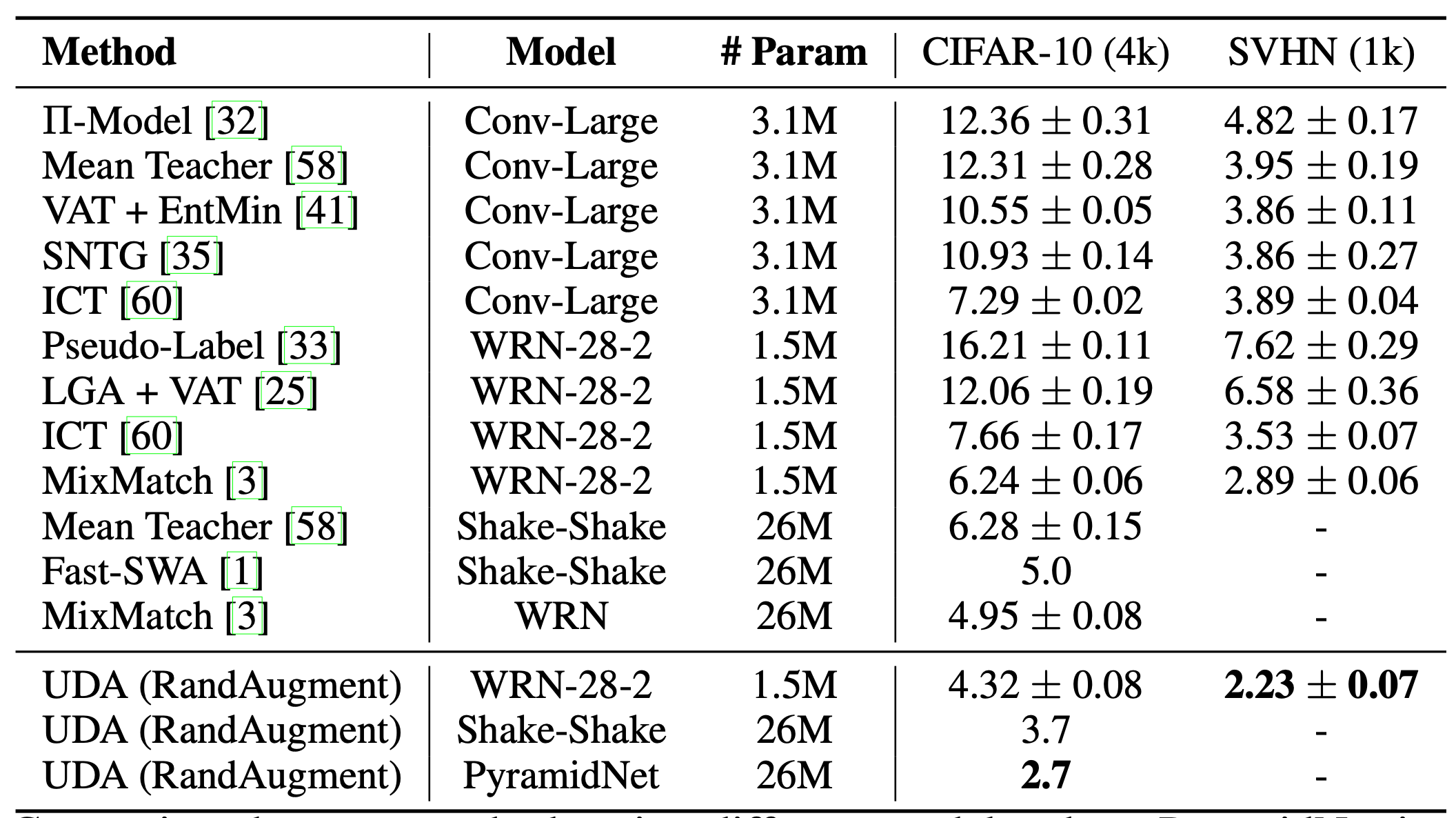
Similar to VAT, Unsupervised Data Augmentation (UDA; Xie et al. 2020) learns to predict the same output for an unlabeled example and the augmented one. UDA especially focuses on studying how the “quality” of noise can impact the semi-supervised learning performance with consistency training. It is crucial to use advanced data augmentation methods for producing meaningful and effective noisy samples. Good data augmentation should produce valid (i.e. does not change the label) and diverse noise, and carry targeted inductive biases.
For images, UDA adopts RandAugment (Cubuk et al. 2019) which uniformly samples augmentation operations available in PIL, no learning or optimization, so it is much cheaper than AutoAugment.
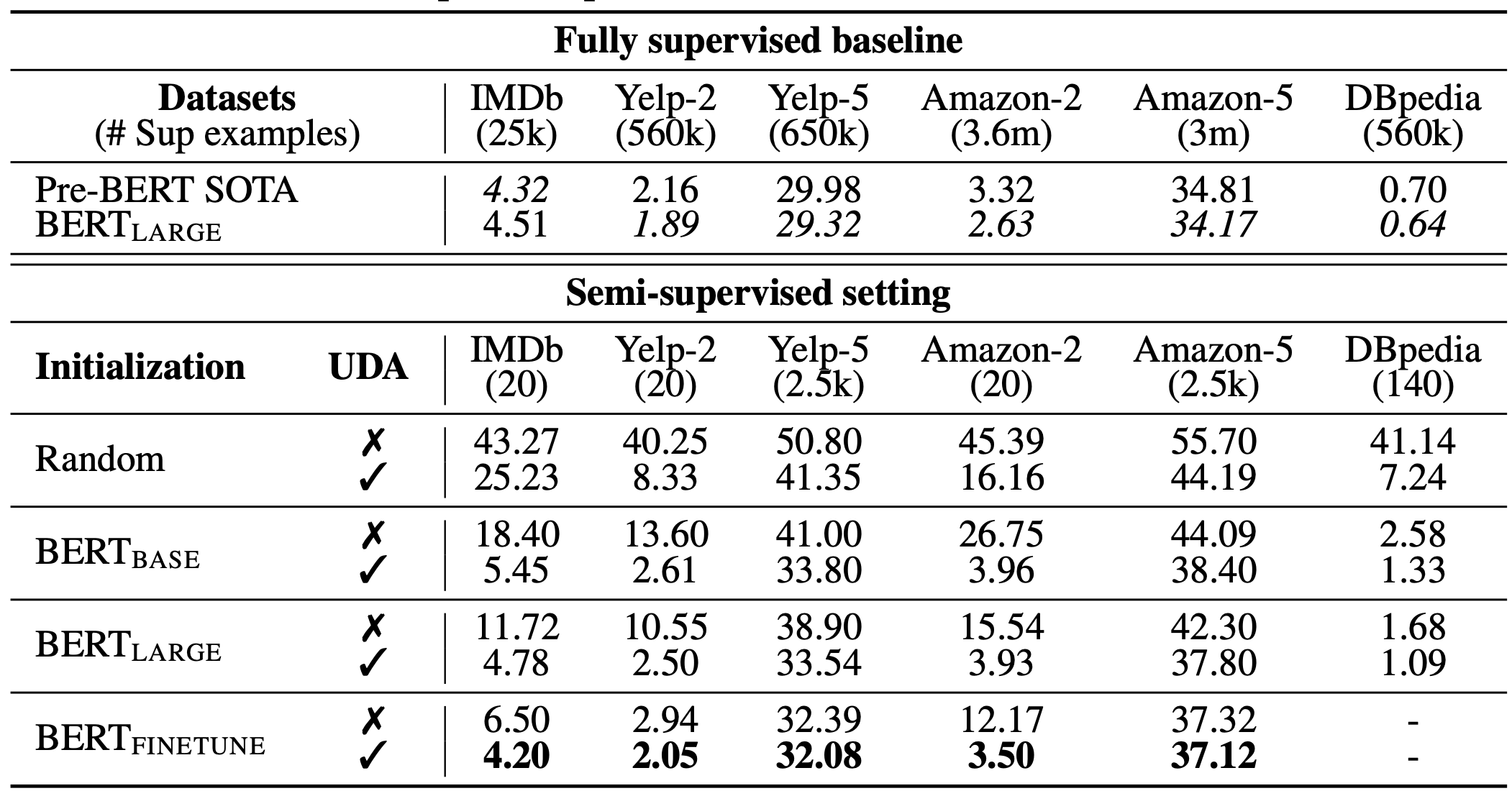
For language, UDA combines back-translation and TF-IDF based word replacement. Back-translation preserves the high-level meaning but may not retain certain words, while TF-IDF based word replacement drops uninformative words with low TF-IDF scores. In the experiments on language tasks, they found UDA to be complementary to transfer learning and representation learning; For example, BERT fine-tuned (i.e. $\text{BERT}_\text{FINETUNE}$ in Fig. 8.) on in-domain unlabeled data can further improve the performance.
When calculating $\mathcal{L}_u$, UDA found two training techniques to help improve the results.
- Low confidence masking: Mask out examples with low prediction confidence if lower than a threshold $\tau$.
- Sharpening prediction distribution: Use a low temperature $T$ in softmax to sharpen the predicted probability distribution.
- In-domain data filtration: In order to extract more in-domain data from a large out-of-domain dataset, they trained a classifier to predict in-domain labels and then retain samples with high confidence predictions as in-domain candidates.
where $\hat{\theta}$ is a fixed copy of model weights, same as in VAT, so no gradient update, and $\bar{\mathbf{x}}$ is the augmented data point. $\tau$ is the prediction confidence threshold and $T$ is the distribution sharpening temperature.
Pseudo Labeling
Pseudo Labeling (Lee 2013) assigns fake labels to unlabeled samples based on the maximum softmax probabilities predicted by the current model and then trains the model on both labeled and unlabeled samples simultaneously in a pure supervised setup.
Why could pseudo labels work? Pseudo label is in effect equivalent to Entropy Regularization (Grandvalet & Bengio 2004), which minimizes the conditional entropy of class probabilities for unlabeled data to favor low density separation between classes. In other words, the predicted class probabilities is in fact a measure of class overlap, minimizing the entropy is equivalent to reduced class overlap and thus low density separation.
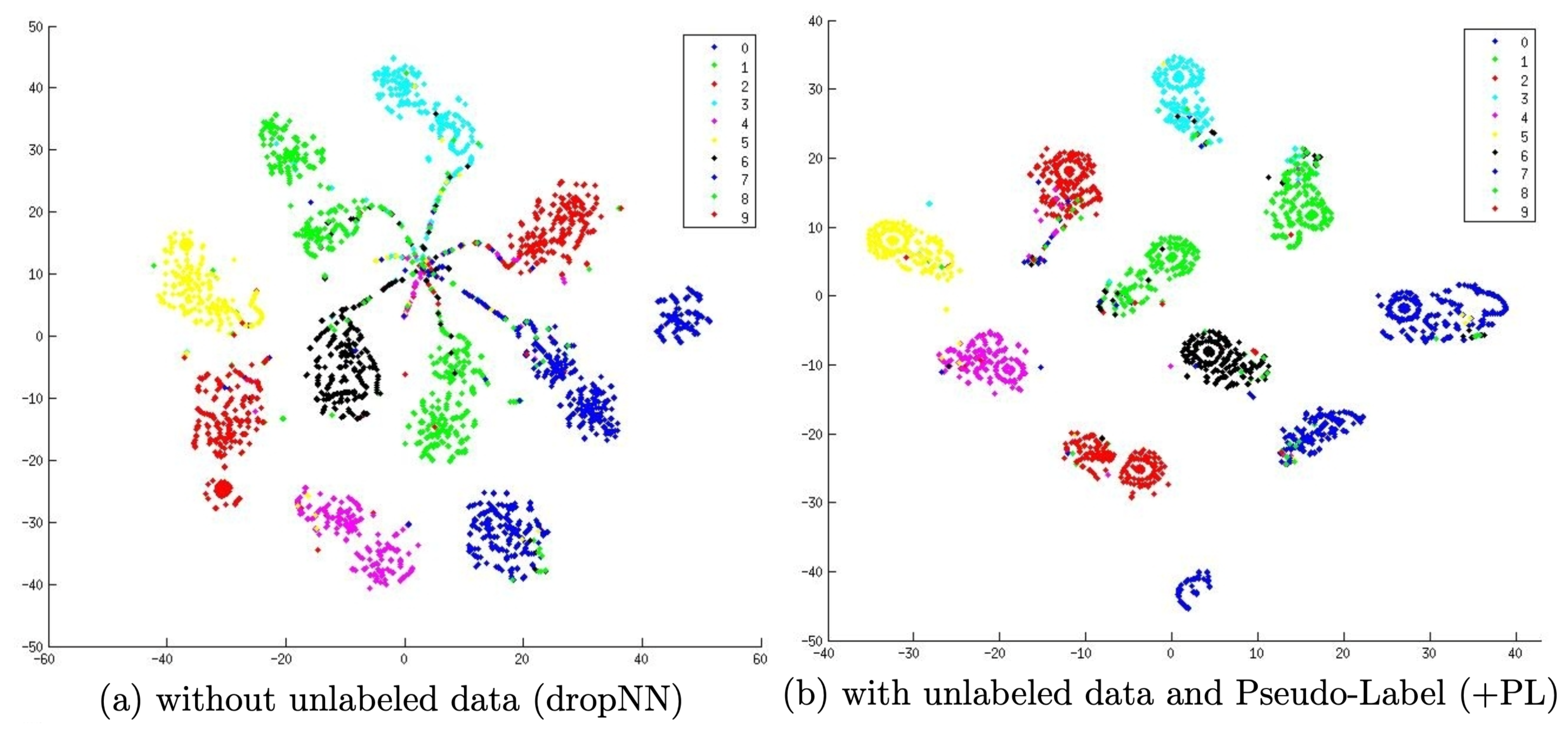
Training with pseudo labeling naturally comes as an iterative process. We refer to the model that produces pseudo labels as teacher and the model that learns with pseudo labels as student.
Label propagation
Label Propagation (Iscen et al. 2019) is an idea to construct a similarity graph among samples based on feature embedding. Then the pseudo labels are “diffused” from known samples to unlabeled ones where the propagation weights are proportional to pairwise similarity scores in the graph. Conceptually it is similar to a k-NN classifier and both suffer from the problem of not scaling up well with a large dataset.
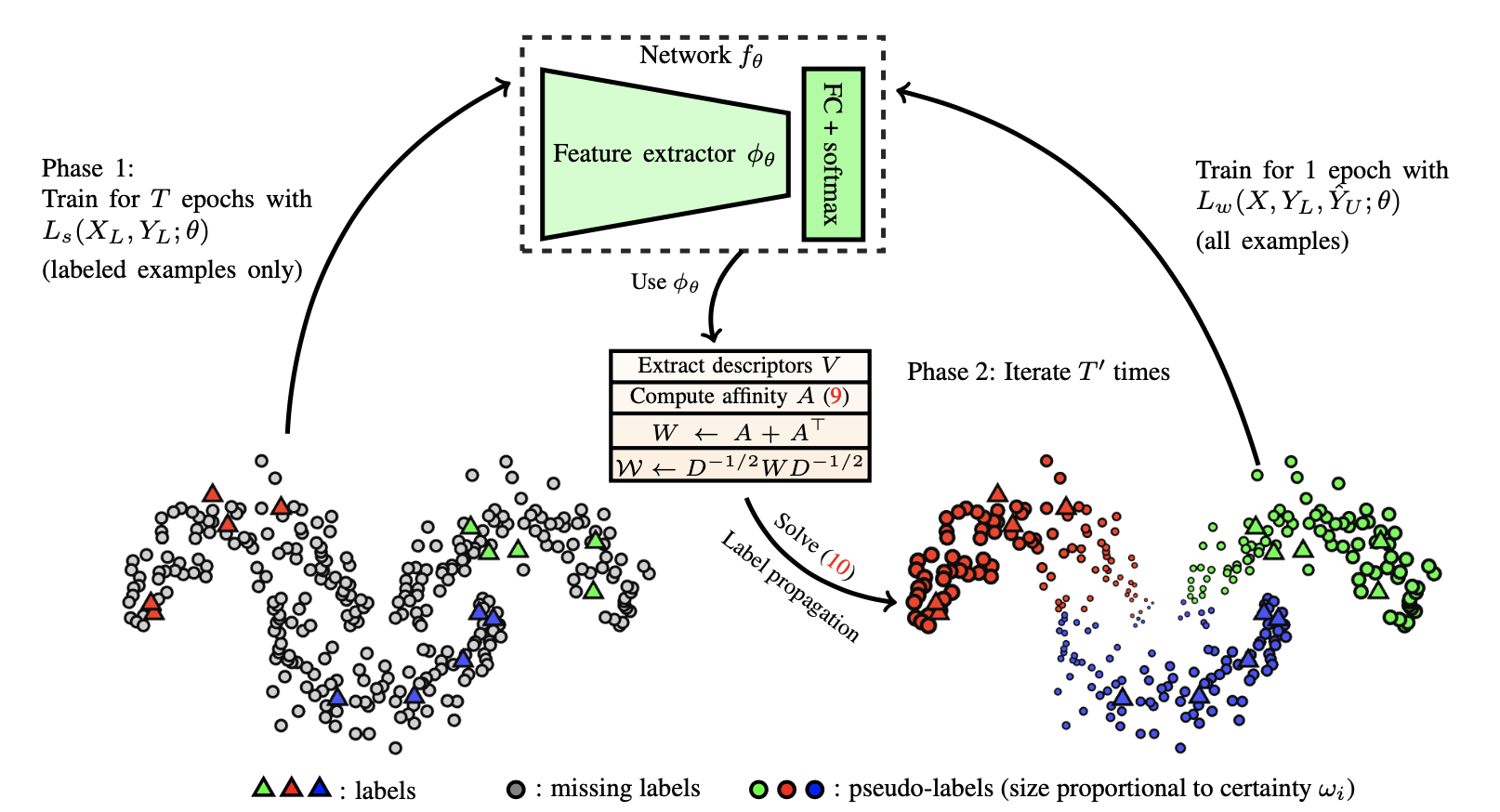
Self-Training
Self-Training is not a new concept (Scudder 1965, Nigram & Ghani CIKM 2000). It is an iterative algorithm, alternating between the following two steps until every unlabeled sample has a label assigned:
- Initially it builds a classifier on labeled data.
- Then it uses this classifier to predict labels for the unlabeled data and converts the most confident ones into labeled samples.
Xie et al. (2020) applied self-training in deep learning and achieved great results. On the ImageNet classification task, they first trained an EfficientNet (Tan & Le 2019) model as teacher to generate pseudo labels for 300M unlabeled images and then trained a larger EfficientNet as student to learn with both true labeled and pseudo labeled images. One critical element in their setup is to have noise during student model training but have no noise for the teacher to produce pseudo labels. Thus their method is called Noisy Student. They applied stochastic depth (Huang et al. 2016), dropout and RandAugment to noise the student. Noise is important for the student to perform better than the teacher. The added noise has a compound effect to encourage the model’s decision making frontier to be smooth, on both labeled and unlabeled data.
A few other important technical configs in noisy student self-training are:
- The student model should be sufficiently large (i.e. larger than the teacher) to fit more data.
- Noisy student should be paired with data balancing, especially important to balance the number of pseudo labeled images in each class.
- Soft pseudo labels work better than hard ones.
Noisy student also improves adversarial robustness against an FGSM (Fast Gradient Sign Attack = The attack uses the gradient of the loss w.r.t the input data and adjusts the input data to maximize the loss) attack though the model is not optimized for adversarial robustness.
SentAugment, proposed by Du et al. (2020), aims to solve the problem when there is not enough in-domain unlabeled data for self-training in the language domain. It relies on sentence embedding to find unlabeled in-domain samples from a large corpus and uses the retrieved sentences for self-training.
Reducing confirmation bias
Confirmation bias is a problem with incorrect pseudo labels provided by an imperfect teacher model. Overfitting to wrong labels may not give us a better student model.
To reduce confirmation bias, Arazo et al. (2019) proposed two techniques. One is to adopt MixUp with soft labels. Given two samples, $(\mathbf{x}_i, \mathbf{x}_j)$ and their corresponding true or pseudo labels $(y_i, y_j)$, the interpolated label equation can be translated to a cross entropy loss with softmax outputs:
Mixup is insufficient if there are too few labeled samples. They further set a minimum number of labeled samples in every mini batch by oversampling the labeled samples. This works better than upweighting labeled samples, because it leads to more frequent updates rather than few updates of larger magnitude which could be less stable. Like consistency regularization, data augmentation and dropout are also important for pseudo labeling to work well.
Meta Pseudo Labels (Pham et al. 2021) adapts the teacher model constantly with the feedback of how well the student performs on the labeled dataset. The teacher and the student are trained in parallel, where the teacher learns to generate better pseudo labels and the student learns from the pseudo labels.
Let the teacher and student model weights be $\theta_T$ and $\theta_S$, respectively. The student model’s loss on the labeled samples is defined as a function $\theta^\text{PL}_S(.)$ of $\theta_T$ and we would like to minimize this loss by optimizing the teacher model accordingly.
However, it is not trivial to optimize the above equation. Borrowing the idea of MAML, it approximates the multi-step $\arg\min_{\theta_S}$ with the one-step gradient update of $\theta_S$,
With soft pseudo labels, the above objective is differentiable. But if using hard pseudo labels, it is not differentiable and thus we need to use RL, e.g. REINFORCE.
The optimization procedure is alternative between training two models:
- Student model update: Given a batch of unlabeled samples $\{ \mathbf{u} \}$, we generate pseudo labels by $f_{\theta_T}(\mathbf{u})$ and optimize $\theta_S$ with one step SGD: $\theta’_S = \color{green}{\theta_S - \eta_S \cdot \nabla_{\theta_S} \mathcal{L}_u(\theta_T, \theta_S)}$.
- Teacher model update: Given a batch of labeled samples $\{(\mathbf{x}^l, y)\}$, we reuse the student’s update to optimize $\theta_T$: $\theta’_T = \theta_T - \eta_T \cdot \nabla_{\theta_T} \mathcal{L}_s ( \color{green}{\theta_S - \eta_S \cdot \nabla_{\theta_S} \mathcal{L}_u(\theta_T, \theta_S)} )$. In addition, the UDA objective is applied to the teacher model to incorporate consistency regularization.
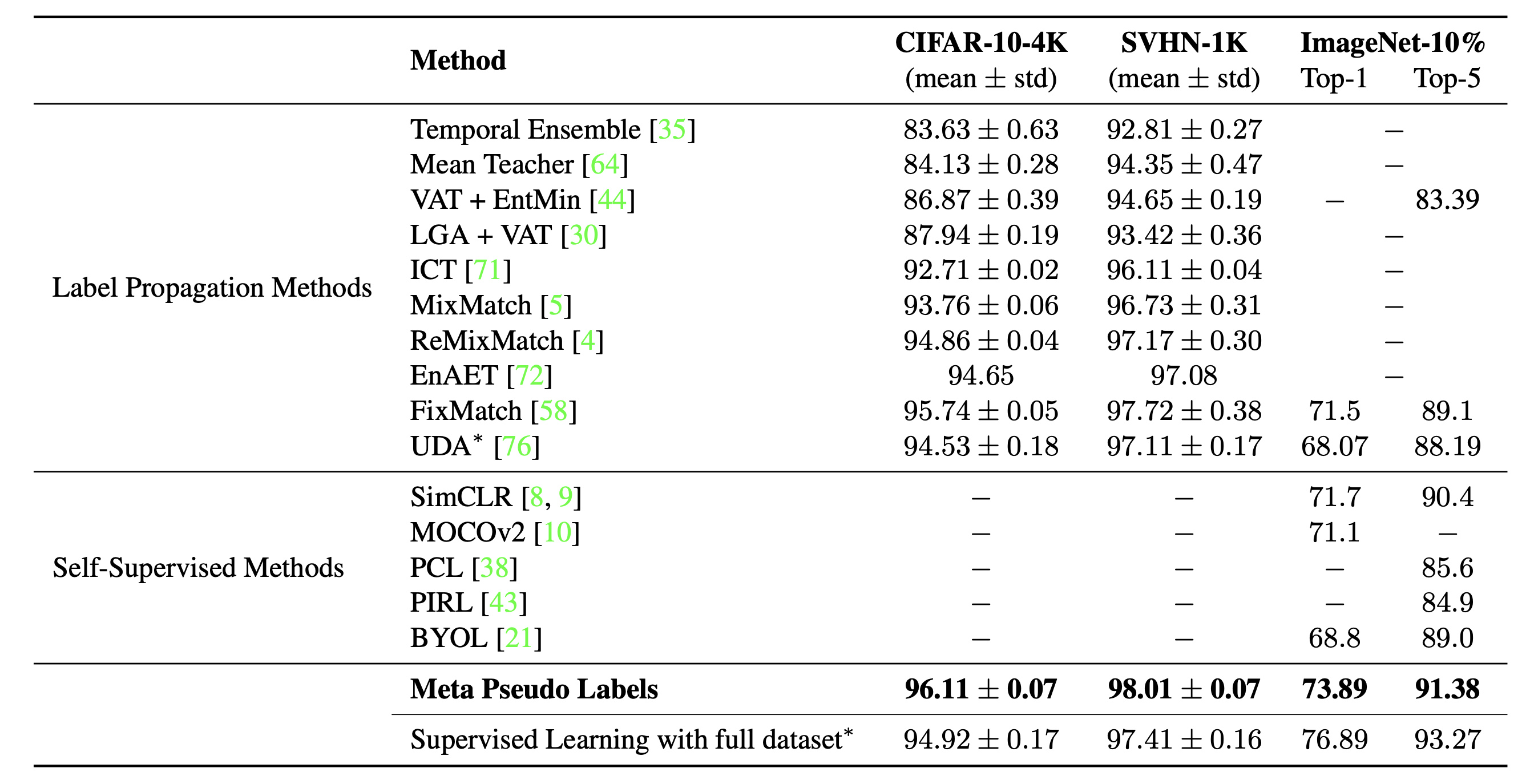
Pseudo Labeling with Consistency Regularization
It is possible to combine the above two approaches together, running semi-supervised learning with both pseudo labeling and consistency training.
MixMatch
MixMatch (Berthelot et al. 2019), as a holistic approach to semi-supervised learning, utilizes unlabeled data by merging the following techniques:
- Consistency regularization: Encourage the model to output the same predictions on perturbed unlabeled samples.
- Entropy minimization: Encourage the model to output confident predictions on unlabeled data.
- MixUp augmentation: Encourage the model to have linear behaviour between samples.
Given a batch of labeled data $\mathcal{X}$ and unlabeled data $\mathcal{U}$, we create augmented versions of them via $\text{MixMatch}(.)$, $\bar{\mathcal{X}}$ and $\bar{\mathcal{U}}$, containing augmented samples and guessed labels for unlabeled examples.
where $T$ is the sharpening temperature to reduce the guessed label overlap; $K$ is the number of augmentations generated per unlabeled example; $\alpha$ is the parameter in MixUp.
For each $\mathbf{u}$, MixMatch generates $K$ augmentations, $\bar{\mathbf{u}}^{(k)} = \text{Augment}(\mathbf{u})$ for $k=1, \dots, K$ and the pseudo label is guessed based on the average: $\hat{y} = \frac{1}{K} \sum_{k=1}^K p_\theta(y \mid \bar{\mathbf{u}}^{(k)})$.
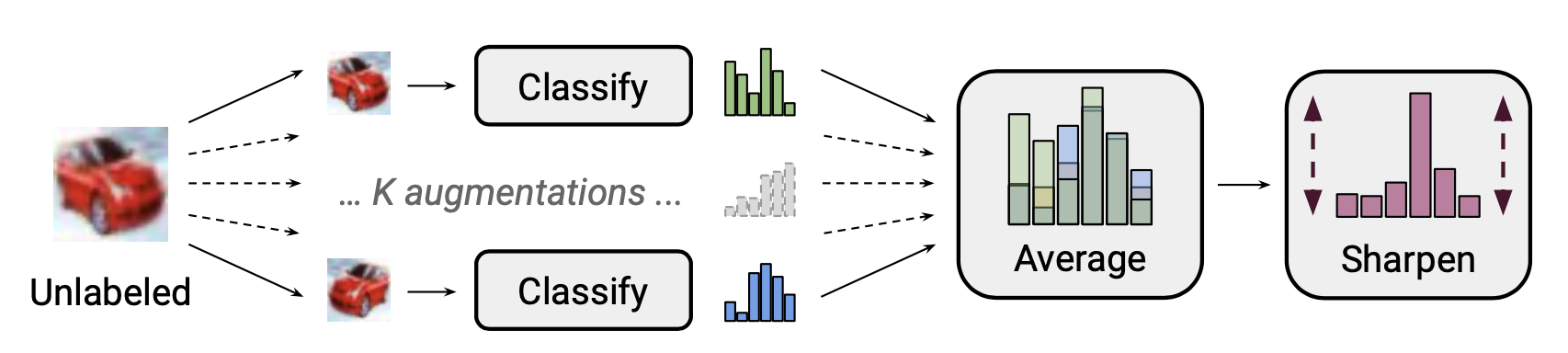
According to their ablation studies, it is critical to have MixUp especially on the unlabeled data. Removing temperature sharpening on the pseudo label distribution hurts the performance quite a lot. Average over multiple augmentations for label guessing is also necessary.
ReMixMatch (Berthelot et al. 2020) improves MixMatch by introducing two new mechanisms:
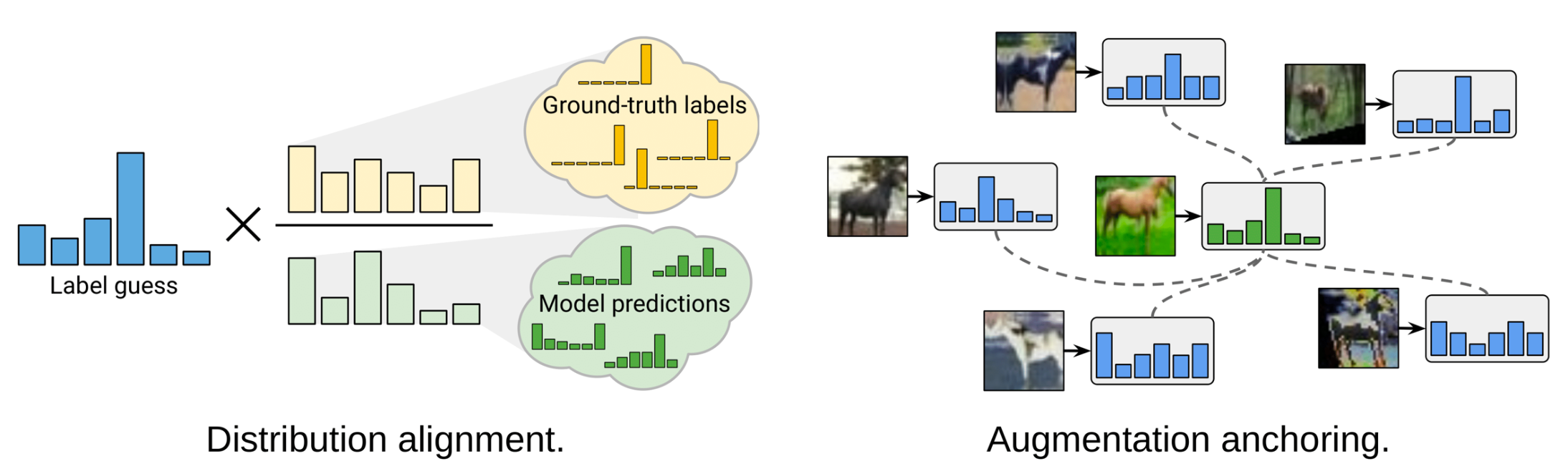
- Distribution alignment. It encourages the marginal distribution $p(y)$ to be close to the marginal distribution of the ground truth labels. Let $p(y)$ be the class distribution in the true labels and $\tilde{p}(\hat{y})$ be a running average of the predicted class distribution among the unlabeled data. The model prediction on an unlabeled sample $p_\theta(y \vert \mathbf{u})$ is normalized to be $\text{Normalize}\big( \frac{p_\theta(y \vert \mathbf{u}) p(y)}{\tilde{p}(\hat{y})} \big)$ to match the true marginal distribution.
- Note that entropy minimization is not a useful objective if the marginal distribution is not uniform.
- I do feel the assumption that the class distributions on the labeled and unlabeled data should match is too strong and not necessarily to be true in the real-world setting.
- Augmentation anchoring. Given an unlabeled sample, it first generates an “anchor” version with weak augmentation and then averages $K$ strongly augmented versions using CTAugment (Control Theory Augment). CTAugment only samples augmentations that keep the model predictions within the network tolerance.
The ReMixMatch loss is a combination of several terms,
- a supervised loss with data augmentation and MixUp applied;
- an unsupervised loss with data augmentation and MixUp applied, using pseudo labels as targets;
- a CE loss on a single heavily-augmented unlabeled image without MixUp;
- a rotation loss as in self-supervised learning.
DivideMix
DivideMix (Junnan Li et al. 2020) combines semi-supervised learning with Learning with noisy labels (LNL). It models the per-sample loss distribution via a GMM to dynamically divide the training data into a labeled set with clean examples and an unlabeled set with noisy ones. Following the idea in Arazo et al. 2019, they fit a two-component GMM on the per-sample cross entropy loss $\ell_i = y_i^\top \log f_\theta(\mathbf{x}_i)$. Clean samples are expected to get lower loss faster than noisy samples. The component with smaller mean is the cluster corresponding to clean labels and let’s denote it as $c$. If the GMM posterior probability $w_i = p_\text{GMM}(c \mid \ell_i)$ (i.e. the probability of the sampling belonging to the clean sample set) is larger than the threshold $\tau$, this sample is considered as a clean sample and otherwise a noisy one.
The data clustering step is named co-divide. To avoid confirmation bias, DivideMix simultaneously trains two diverged networks where each network uses the dataset division from the other network; e.g. thinking about how Double Q Learning works.
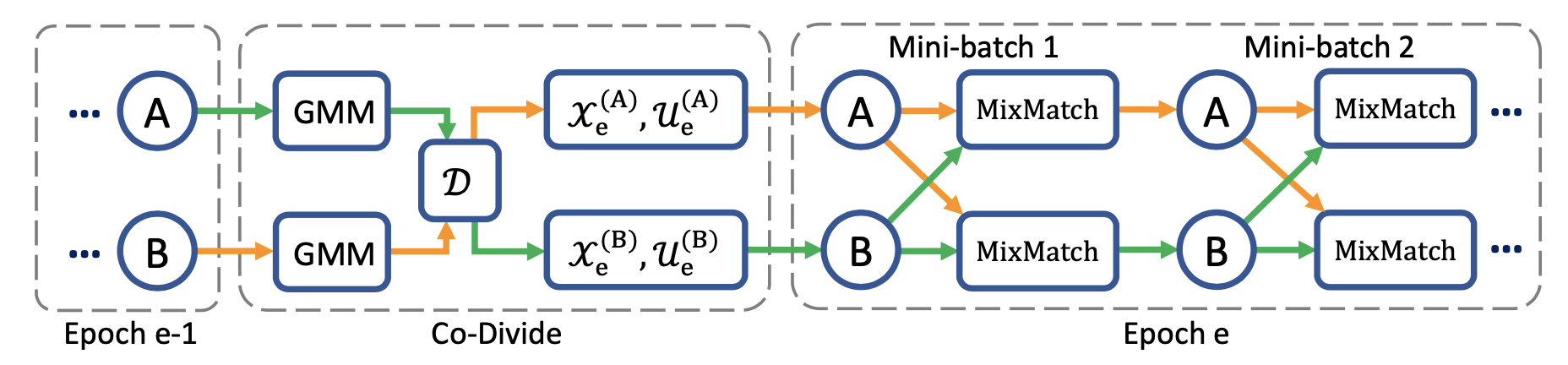
Compared to MixMatch, DivideMix has an additional co-divide stage for handling noisy samples, as well as the following improvements during training:
- Label co-refinement: It linearly combines the ground-truth label $y_i$ with the network’s prediction $\hat{y}_i$, which is averaged across multiple augmentations of $\mathbf{x}_i$, guided by the clean set probability $w_i$ produced by the other network.
- Label co-guessing: It averages the predictions from two models for unlabelled data samples.

FixMatch
FixMatch (Sohn et al. 2020) generates pseudo labels on unlabeled samples with weak augmentation and only keeps predictions with high confidence. Here both weak augmentation and high confidence filtering help produce high-quality trustworthy pseudo label targets. Then FixMatch learns to predict these pseudo labels given a heavily-augmented sample.
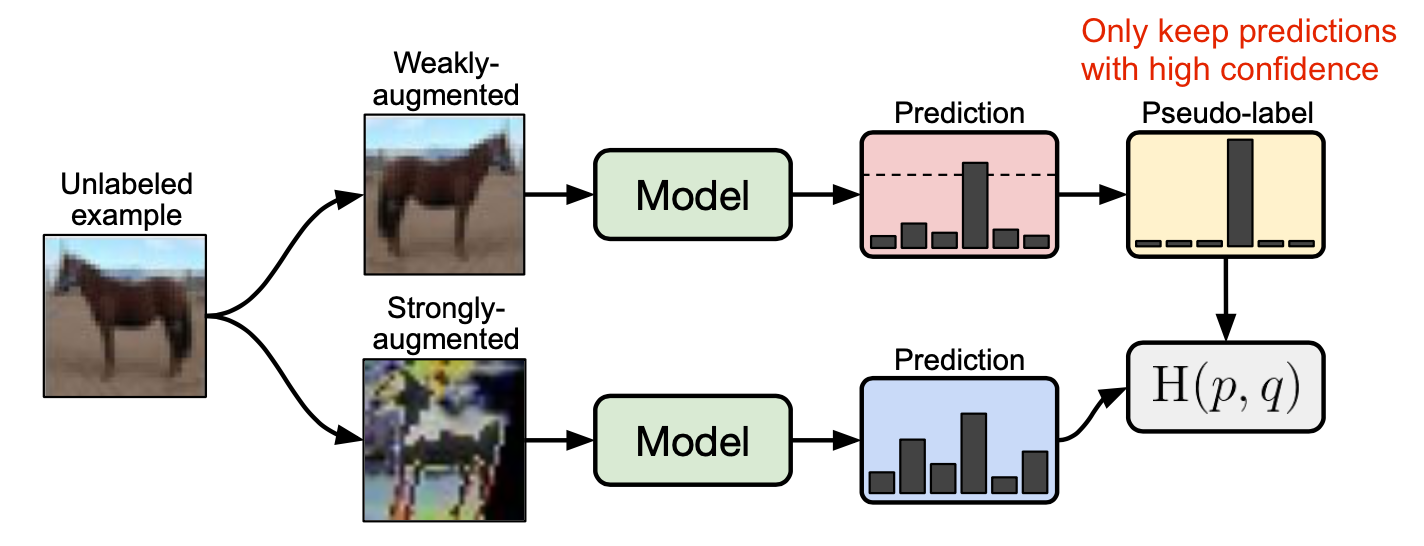
where $\hat{y}_b$ is the pseudo label for an unlabeled example; $\mu$ is a hyperparameter that determines the relative sizes of $\mathcal{X}$ and $\mathcal{U}$.
- Weak augmentation $\mathcal{A}_\text{weak}(.)$: A standard flip-and-shift augmentation
- Strong augmentation $\mathcal{A}_\text{strong}(.)$ : AutoAugment, Cutout, RandAugment, CTAugment
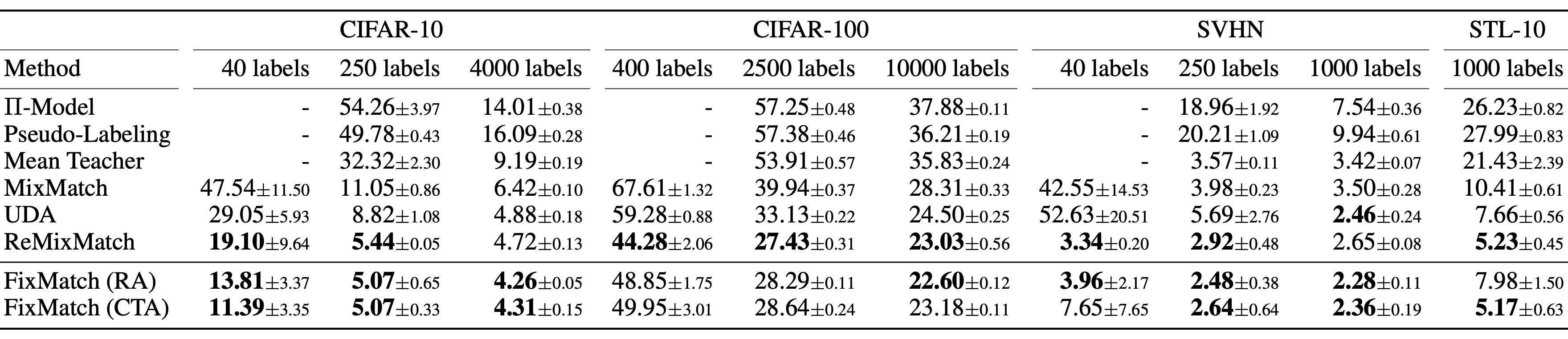
According to the ablation studies of FixMatch,
- Sharpening the predicted distribution with a temperature parameter $T$ does not have a significant impact when the threshold $\tau$ is used.
- Cutout and CTAugment as part of strong augmentations are necessary for good performance.
- When the weak augmentation for label guessing is replaced with strong augmentation, the model diverges early in training. If discarding weak augmentation completely, the model overfit the guessed labels.
- Using weak instead of strong augmentation for pseudo label prediction leads to unstable performance. Strong data augmentation is critical.
Combined with Powerful Pre-Training
It is a common paradigm, especially in language tasks, to first pre-train a task-agnostic model on a large unsupervised data corpus via self-supervised learning and then fine-tune it on the downstream task with a small labeled dataset. Research has shown that we can obtain extra gain if combining semi-supervised learning with pretraining.
Zoph et al. (2020) studied to what degree self-training can work better than pre-training. Their experiment setup was to use ImageNet for pre-training or self-training to improve COCO. Note that when using ImageNet for self-training, it discards labels and only uses ImageNet samples as unlabeled data points. He et al. (2018) has demonstrated that ImageNet classification pre-training does not work well if the downstream task is very different, such as object detection.
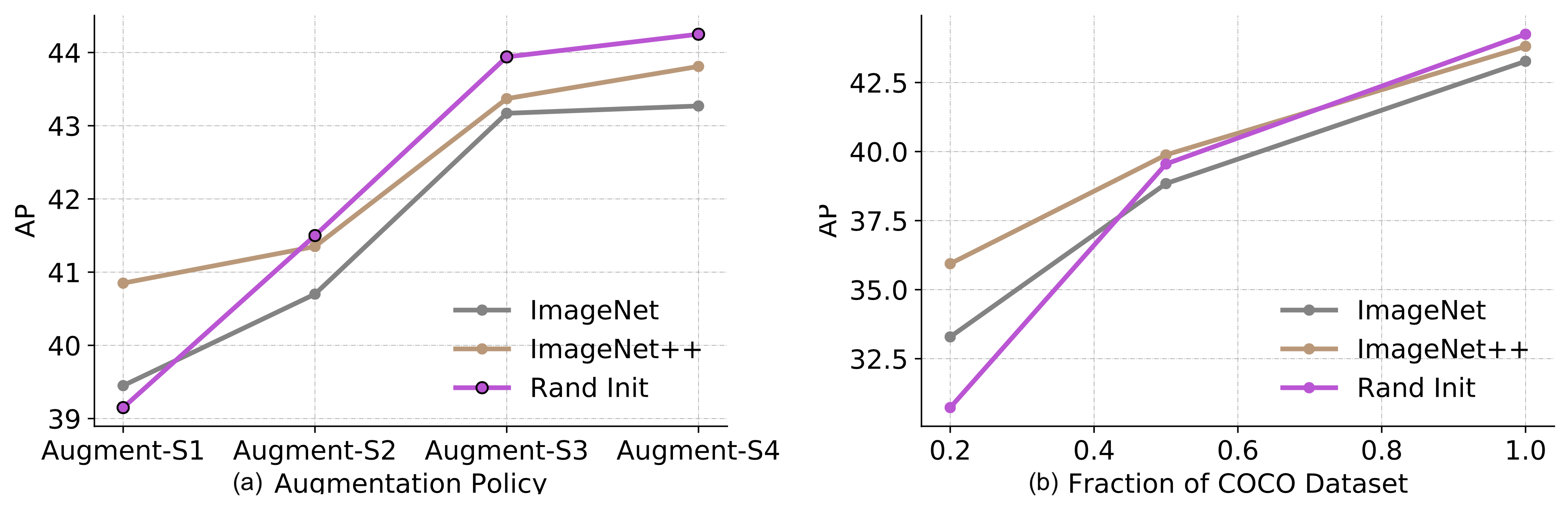
Their experiments demonstrated a series of interesting findings:
- The effectiveness of pre-training diminishes with more labeled samples available for the downstream task. Pre-training is helpful in the low-data regimes (20%) but neutral or harmful in the high-data regime.
- Self-training helps in high data/strong augmentation regimes, even when pre-training hurts.
- Self-training can bring in additive improvement on top of pre-training, even using the same data source.
- Self-supervised pre-training (e.g. via SimCLR) hurts the performance in a high data regime, similar to how supervised pre-training does.
- Joint-training supervised and self-supervised objectives help resolve the mismatch between the pre-training and downstream tasks. Pre-training, joint-training and self-training are all additive.
- Noisy labels or un-targeted labeling (i.e. pre-training labels are not aligned with downstream task labels) is worse than targeted pseudo labeling.
- Self-training is computationally more expensive than fine-tuning on a pre-trained model.
Chen et al. (2020) proposed a three-step procedure to merge the benefits of self-supervised pretraining, supervised fine-tuning and self-training together:
- Unsupervised or self-supervised pretrain a big model.
- Supervised fine-tune it on a few labeled examples. It is important to use a big (deep and wide) neural network. Bigger models yield better performance with fewer labeled samples.
- Distillation with unlabeled examples by adopting pseudo labels in self-training.
- It is possible to distill the knowledge from a large model into a small one because the task-specific use does not require extra capacity of the learned representation.
- The distillation loss is formatted as the following, where the teacher network is fixed with weights $\hat{\theta}_T$.
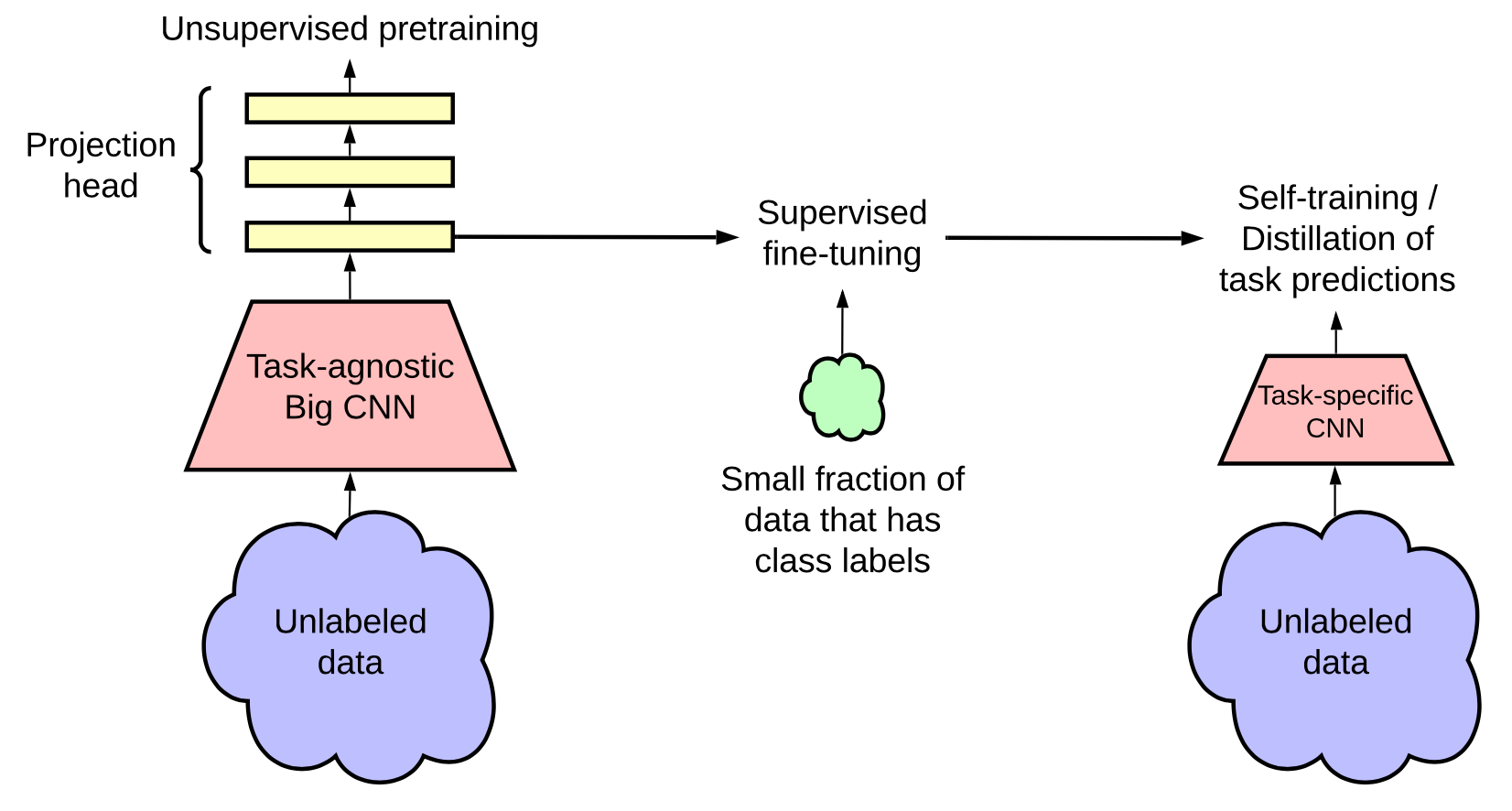
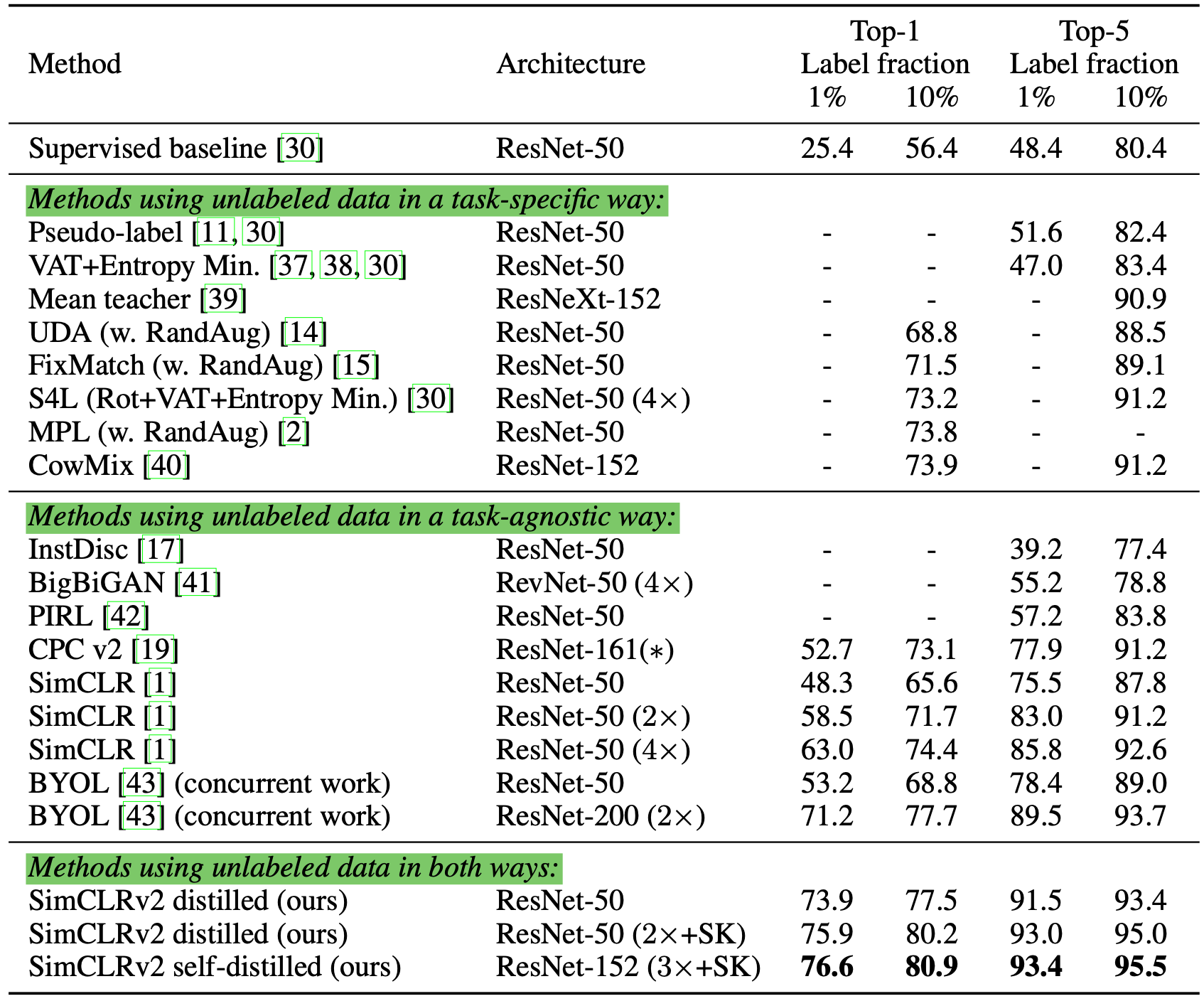
They experimented on the ImageNet classification task. The self-supervised pre-training uses SimCLRv2, a directly improved version of SimCLR. Observations in their empirical studies confirmed several learnings, aligned with Zoph et al. 2020:
- Bigger models are more label-efficient;
- Bigger/deeper project heads in SimCLR improve representation learning;
- Distillation using unlabeled data improves semi-supervised learning.
💡 Quick summary of common themes among recent semi-supervised learning methods, many aiming to reduce confirmation bias:
- Apply valid and diverse noise to samples by advanced data augmentation methods.
- When dealing with images, MixUp is an effective augmentation. Mixup could work on language too, resulting in a small incremental improvement (Guo et al. 2019).
- Set a threshold and discard pseudo labels with low confidence.
- Set a minimum number of labeled samples per mini-batch.
- Sharpen the pseudo label distribution to reduce the class overlap.
Citation
Cited as:
Weng, Lilian. (Dec 2021). Learning with not enough data part 1: semi-supervised learning. Lil’Log. https://lilianweng.github.io/posts/2021-12-05-semi-supervised/.
Or
@article{weng2021semi,
title = "Learning with not Enough Data Part 1: Semi-Supervised Learning",
author = "Weng, Lilian",
journal = "lilianweng.github.io",
year = "2021",
month = "Dec",
url = "https://lilianweng.github.io/posts/2021-12-05-semi-supervised/"
}
References
[1] Ouali, Hudelot & Tami. “An Overview of Deep Semi-Supervised Learning” arXiv preprint arXiv:2006.05278 (2020).
[2] Sajjadi, Javanmardi & Tasdizen “Regularization With Stochastic Transformations and Perturbations for Deep Semi-Supervised Learning.” arXiv preprint arXiv:1606.04586 (2016).
[3] Pham et al. “Meta Pseudo Labels.” CVPR 2021.
[4] Laine & Aila. “Temporal Ensembling for Semi-Supervised Learning” ICLR 2017.
[5] Tarvaninen & Valpola. “Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results.” NeuriPS 2017
[6] Xie et al. “Unsupervised Data Augmentation for Consistency Training.” NeuriPS 2020.
[7] Miyato et al. “Virtual Adversarial Training: A Regularization Method for Supervised and Semi-Supervised Learning.” IEEE transactions on pattern analysis and machine intelligence 41.8 (2018).
[8] Verma et al. “Interpolation consistency training for semi-supervised learning.” IJCAI 2019
[9] Lee. “Pseudo-label: The simple and efficient semi-supervised learning method for deep neural networks.” ICML 2013 Workshop: Challenges in Representation Learning.
[10] Iscen et al. “Label propagation for deep semi-supervised learning.” CVPR 2019.
[11] Xie et al. “Self-training with Noisy Student improves ImageNet classification” CVPR 2020.
[12] Jingfei Du et al. “Self-training Improves Pre-training for Natural Language Understanding.” 2020
[13] Iscen et al. “Label propagation for deep semi-supervised learning.” CVPR 2019
[14] Arazo et al. “Pseudo-labeling and confirmation bias in deep semi-supervised learning.” IJCNN 2020.
[15] Berthelot et al. “MixMatch: A holistic approach to semi-supervised learning.” NeuriPS 2019
[16] Berthelot et al. “ReMixMatch: Semi-supervised learning with distribution alignment and augmentation anchoring.” ICLR 2020
[17] Sohn et al. “FixMatch: Simplifying semi-supervised learning with consistency and confidence.” CVPR 2020
[18] Junnan Li et al. “DivideMix: Learning with Noisy Labels as Semi-supervised Learning.” 2020 [code]
[19] Zoph et al. “Rethinking pre-training and self-training.” 2020.
[20] Chen et al. “Big Self-Supervised Models are Strong Semi-Supervised Learners” 2020