This is part 2 of what to do when facing a limited amount of labeled data for supervised learning tasks. This time we will get some amount of human labeling work involved, but within a budget limit, and therefore we need to be smart when selecting which samples to label.
Notations
| Symbol | Meaning |
|---|---|
| $K$ | Number of unique class labels. |
| $(\mathbf{x}^l, y) \sim \mathcal{X}, y \in \{0, 1\}^K$ | Labeled dataset. $y$ is a one-hot representation of the true label. |
| $\mathbf{u} \sim \mathcal{U}$ | Unlabeled dataset. |
| $\mathcal{D} = \mathcal{X} \cup \mathcal{U}$ | The entire dataset, including both labeled and unlabeled examples. |
| $\mathbf{x}$ | Any sample which can be either labeled or unlabeled. |
| $\mathbf{x}_i$ | The $i$-th sample. |
| $U(\mathbf{x})$ | Scoring function for active learning selection. |
| $P_\theta(y \vert \mathbf{x})$ | A softmax classifier parameterized by $\theta$. |
| $\hat{y} = \arg\max_{y \in \mathcal{Y}} P_\theta(y \vert \mathbf{x})$ | The most confident prediction by the classifier. |
| $B$ | Labeling budget (the maximum number of samples to label). |
| $b$ | Batch size. |
What is Active Learning?
Given an unlabeled dataset $\mathcal{U}$ and a fixed amount of labeling cost $B$, active learning aims to select a subset of $B$ examples from $\mathcal{U}$ to be labeled such that they can result in maximized improvement in model performance. This is an effective way of learning especially when data labeling is difficult and costly, e.g. medical images. This classical survey paper in 2010 lists many key concepts. While some conventional approaches may not apply to deep learning, discussion in this post mainly focuses on deep neural models and training in batch mode.
To simplify the discussion, we assume that the task is a $K$-class classification problem in all the following sections. The model with parameters $\theta$ outputs a probability distribution over the label candidates, which may or may not be calibrated, $P_\theta(y \vert \mathbf{x})$ and the most likely prediction is $\hat{y} = \arg\max_{y \in \mathcal{Y}} P_\theta(y \vert \mathbf{x})$.
Acquisition Function
The process of identifying the most valuable examples to label next is referred to as “sampling strategy” or “query strategy”. The scoring function in the sampling process is named “acquisition function”, denoted as $U(\mathbf{x})$. Data points with higher scores are expected to produce higher value for model training if they get labeled.
Here is a list of basic sampling strategies.
Uncertainty Sampling
Uncertainty sampling selects examples for which the model produces most uncertain predictions. Given a single model, uncertainty can be estimated by the predicted probabilities, although one common complaint is that deep learning model predictions are often not calibrated and not correlated with true uncertainty well. In fact, deep learning models are often overconfident.
- Least confident score, also known as variation ratio: $U(\mathbf{x}) = 1 - P_\theta(\hat{y} \vert \mathbf{x})$.
- Margin score: $U(\mathbf{x}) = P_\theta(\hat{y}_1 \vert \mathbf{x}) - P_\theta(\hat{y}_2 \vert \mathbf{x})$, where $\hat{y}_1$ and $\hat{y}_2$ are the most likely and the second likely predicted labels.
- Entropy: $U(\mathbf{x}) = \mathcal{H}(P_\theta(y \vert \mathbf{x})) = - \sum_{y \in \mathcal{Y}} P_\theta(y \vert \mathbf{x}) \log P_\theta(y \vert \mathbf{x})$.
Another way to quantify uncertainty is to rely on a committee of expert models, known as Query-By-Committee (QBC). QBC measures uncertainty based on a pool of opinions and thus it is critical to keep a level of disagreement among committee members. Given $C$ models in the committee pool, each parameterized by $\theta_1, \dots, \theta_C$.
- Voter entropy: $U(\mathbf{x}) = \mathcal{H}(\frac{V(y)}{C})$, where $V(y)$ counts the number of votes from the committee on the label $y$.
- Consensus entropy: $U(\mathbf{x}) = \mathcal{H}(P_\mathcal{C})$, where $P_\mathcal{C}$ is the prediction averaging across the committee.
- KL divergence: $U(\mathbf{x}) = \frac{1}{C} \sum_{c=1}^C D_\text{KL} (P_{\theta_c} | P_\mathcal{C})$
Diversity Sampling
Diversity sampling intend to find a collection of samples that can well represent the entire data distribution. Diversity is important because the model is expected to work well on any data in the wild, just not on a narrow subset. Selected samples should be representative of the underlying distribution. Common approaches often rely on quantifying the similarity between samples.
Expected Model Change
Expected model change refers to the impact that a sample brings onto the model training. The impact can be the influence on the model weights or the improvement over the training loss. A later section reviews several works on how to measure model impact triggered by selected data samples.
Hybrid Strategy
Many methods above are not mutually exclusive. A hybrid sampling strategy values different attributes of data points, combining different sampling preferences into one. Often we want to select uncertain but also highly representative samples.
Deep Acquisition Function
Measuring Uncertainty
The model uncertainty is commonly categorized into two buckets (Der Kiureghian & Ditlevsen 2009, Kendall & Gal 2017):
- Aleatoric uncertainty is introduced by noise in the data (e.g. sensor data, noise in the measurement process) and it can be input-dependent or input-independent. It is generally considered as irreducible since there is missing information about the ground truth.
- Epistemic uncertainty refers to the uncertainty within the model parameters and therefore we do not know whether the model can best explain the data. This type of uncertainty is theoretically reducible given more data
Ensemble and Approximated Ensemble
There is a long tradition in machine learning of using ensembles to improve model performance. When there is a significant diversity among models, ensembles are expected to yield better results. This ensemble theory is proved to be correct by many ML algorithms; for example, AdaBoost aggregates many weak learners to perform similar or even better than a single strong learner. Bootstrapping ensembles multiple trials of resampling to achieve more accurate estimation of metrics. Random forests or GBM is also a good example for the effectiveness of ensembling.
To get better uncertainty estimation, it is intuitive to aggregate a collection of independently trained models. However, it is expensive to train a single deep neural network model, let alone many of them. In reinforcement learning, Bootstrapped DQN (Osband, et al. 2016) is equipped with multiple value heads and relies on the uncertainty among an ensemble of Q value approximation to guide exploration in RL.
In active learning, a commoner approach is to use dropout to “simulate” a probabilistic Gaussian process (Gal & Ghahramani 2016). We thus ensemble multiple samples collected from the same model but with different dropout masks applied during the forward pass to estimate the model uncertainty (epistemic uncertainty). The process is named MC dropout (Monte Carlo dropout), where dropout is applied before every weight layer, is approved to be mathematically equivalent to an approximation to the probabilistic deep Gaussian process (Gal & Ghahramani 2016). This simple idea has been shown to be effective for classification with small datasets and widely adopted in scenarios when efficient model uncertainty estimation is needed.
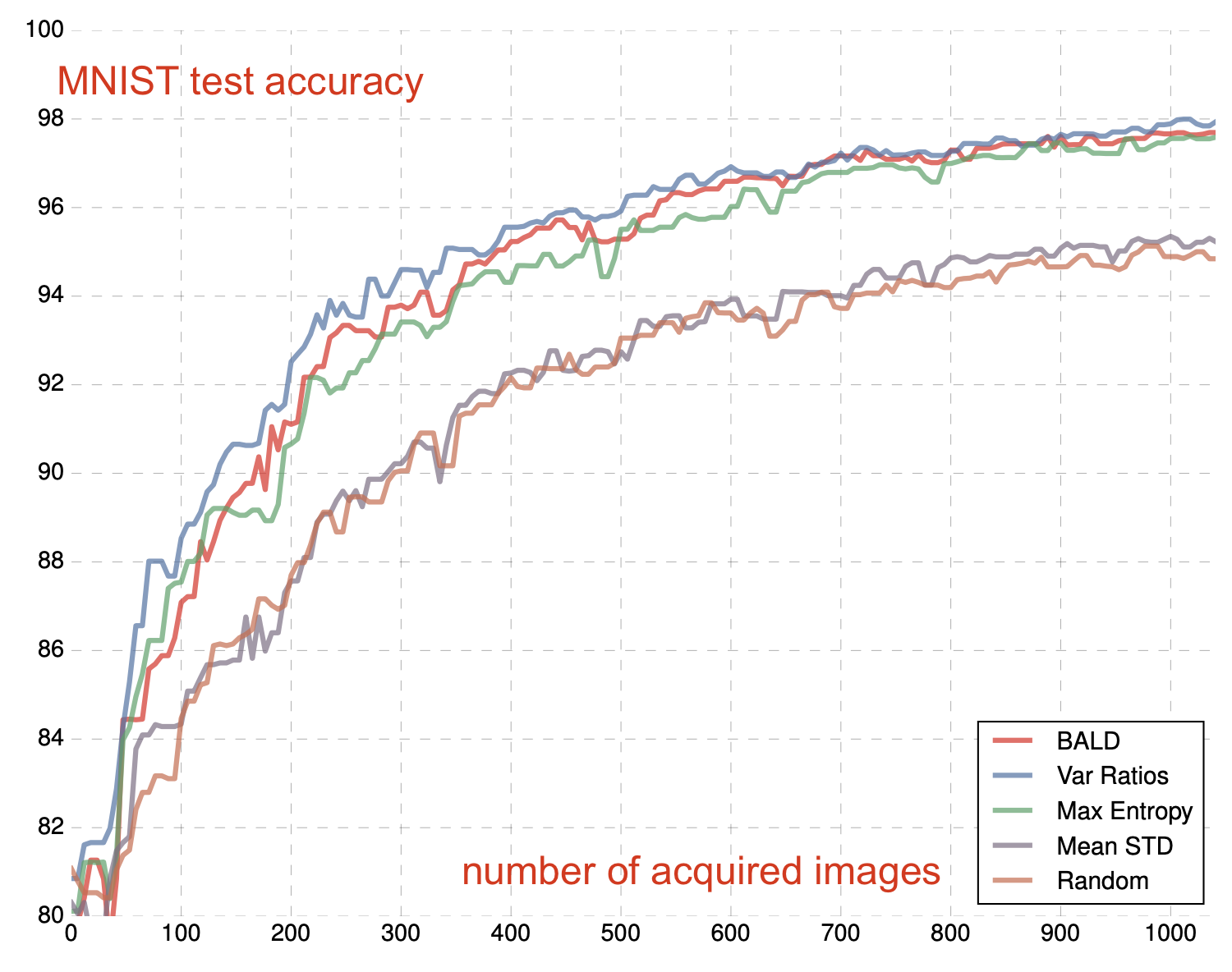
DBAL (Deep Bayesian active learning; Gal et al. 2017) approximates Bayesian neural networks with MC dropout such that it learns a distribution over model weights. In their experiment, MC dropout performed better than random baseline and mean standard deviation (Mean STD), similarly to variation ratios and entropy measurement.
Beluch et al. (2018) compared ensemble-based models with MC dropout and found that the combination of naive ensemble (i.e. train multiple models separately and independently) and variation ratio yields better calibrated predictions than others. However, naive ensembles are very expensive, so they explored a few alternative cheaper options:
- Snapshot ensemble: Use a cyclic learning rate schedule to train an implicit ensemble such that it converges to different local minima.
- Diversity encouraging ensemble (DEE): Use a base network trained for a small number of epochs as initialization for $n$ different networks, each trained with dropout to encourage diversity.
- Split head approach: One base model has multiple heads, each corresponding to one classifier.
Unfortunately all the cheap implicit ensemble options above perform worse than naive ensembles. Considering the limit on computational resources, MC dropout is still a pretty good and economical choice. Naturally, people also try to combine ensemble and MC dropout (Pop & Fulop 2018) to get a bit of additional performance gain by stochastic ensemble.
Uncertainty in Parameter Space
Bayes-by-backprop (Blundell et al. 2015) measures weight uncertainty in neural networks directly. The method maintains a probability distribution over the weights $\mathbf{w}$, which is modeled as a variational distribution $q(\mathbf{w} \vert \theta)$ since the true posterior $p(\mathbf{w} \vert \mathcal{D})$ is not tractable directly. The loss is to minimize the KL divergence between $q(\mathbf{w} \vert \theta)$ and $p(\mathbf{w} \vert \mathcal{D})$,
The variational distribution $q$ is typically a Gaussian with diagonal covariance and each weight is sampled from $\mathcal{N}(\mu_i, \sigma_i^2)$. To ensure non-negativity of $\sigma_i$, it is further parameterized via softplus, $\sigma_i = \log(1 + \exp(\rho_i))$ where the variational parameters are $\theta = \{\mu_i , \rho_i\}^d_{i=1}$.
The process of Bayes-by-backprop can be summarized as:
- Sample $\epsilon \sim \mathcal{N}(0, I)$
- Let $\mathbf{w} = \mu + \log(1+ \exp(\rho)) \circ \epsilon$
- Let $\theta = (\mu, \rho)$
- Let $f(\mathbf{w}, \theta) = \log q(\mathbf{w} \vert \theta) - \log p(\mathbf{w})p(\mathcal{D}\vert \mathbf{w})$
- Calculate the gradient of $f(\mathbf{w}, \theta)$ w.r.t. to $\mu$ and $\rho$ and then update $\theta$.
- Uncertainty is measured by sampling different model weights during inference.
Loss Prediction
The loss objective guides model training. A low loss value indicates that a model can make good and accurate predictions. Yoo & Kweon (2019) designed a loss prediction module to predict the loss value for unlabeled inputs, as an estimation of how good a model prediction is on the given data. Data samples are selected if the loss prediction module makes uncertain predictions (high loss value) for them. The loss prediction module is a simple MLP with dropout, that takes several intermediate layer features as inputs and concatenates them after a global average pooling.
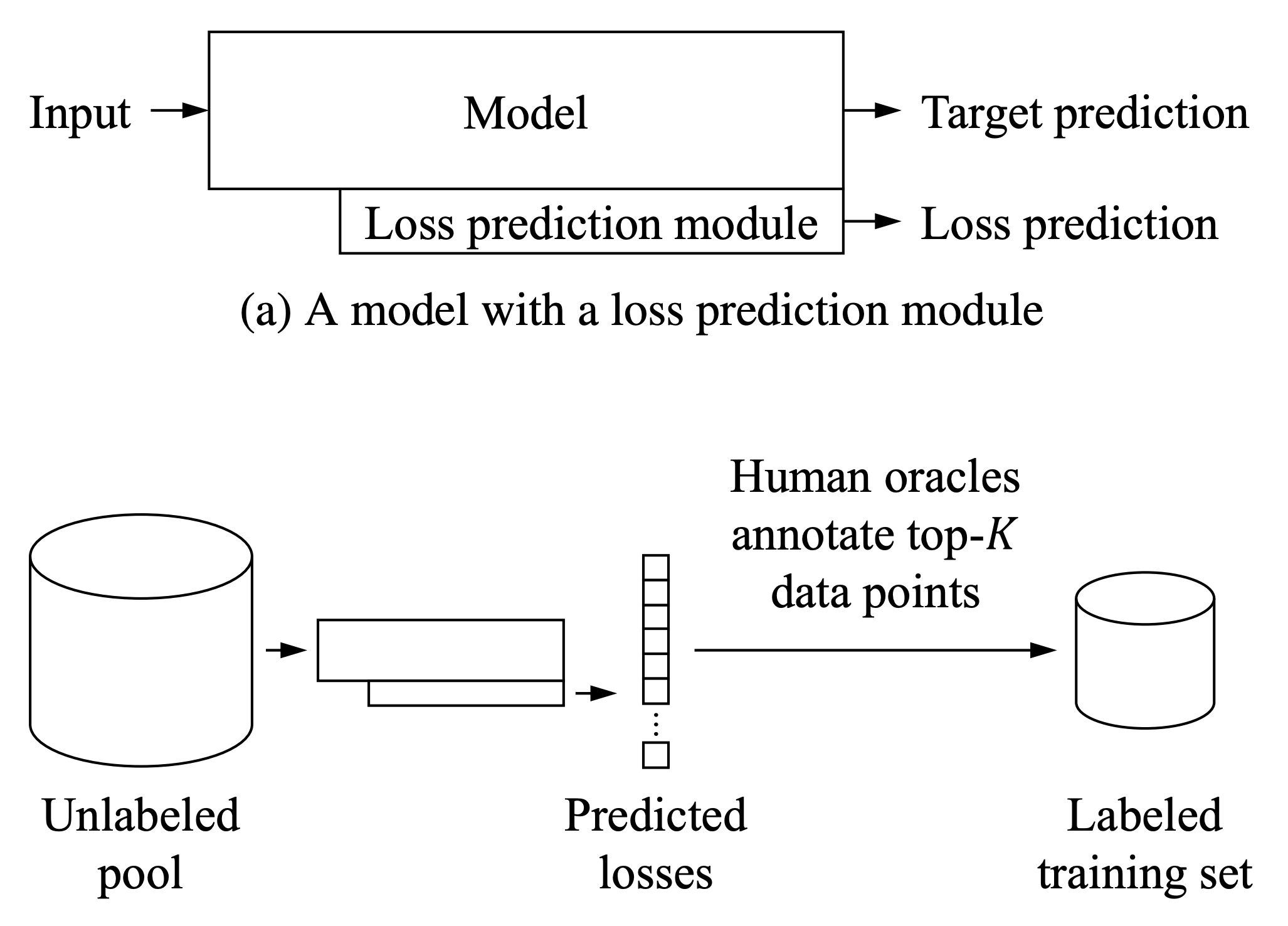
Let $\hat{l}$ be the output of the loss prediction module and $l$ be the true loss. When training the loss prediction module, a simple MSE loss $=(l - \hat{l})^2$ is not a good choice, because the loss decreases in time as the model learns to behave better. A good learning objective should be independent of the scale changes of the target loss. They instead rely on the comparison of sample pairs. Within each batch of size $b$, there are $b/2$ pairs of samples $(\mathbf{x}_i, \mathbf{x}_j)$ and the loss prediction model is expected to correctly predict which sample has a larger loss.
where $\epsilon$ is a predefined positive margin constant.
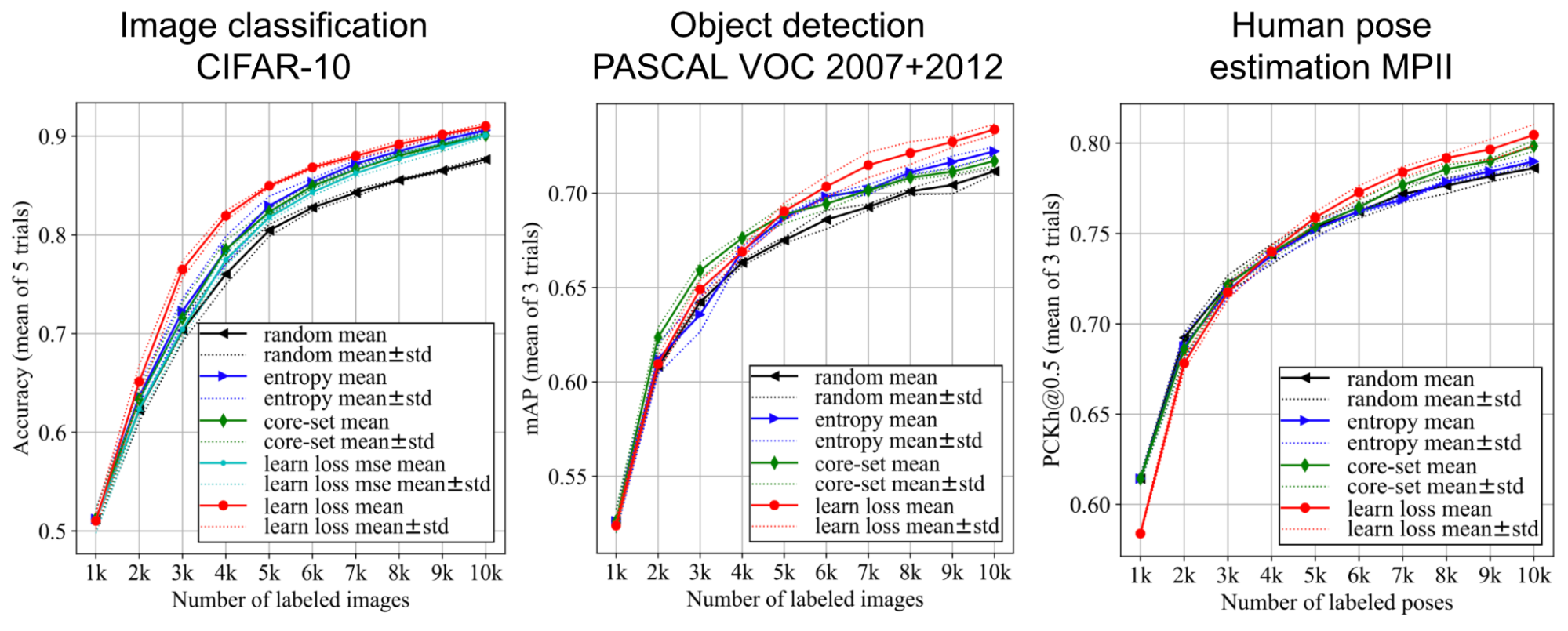
In experiments on three vision tasks, active learning selection based on the loss prediction performs better than random baseline, entropy based acquisition and core-set.
Adversarial Setup
Sinha et al. (2019) proposed a GAN-like setup, named VAAL (Variational Adversarial Active Learning), where a discriminator is trained to distinguish unlabeled data from labeled data. Interestingly, active learning acquisition criteria does not depend on the task performance in VAAL.
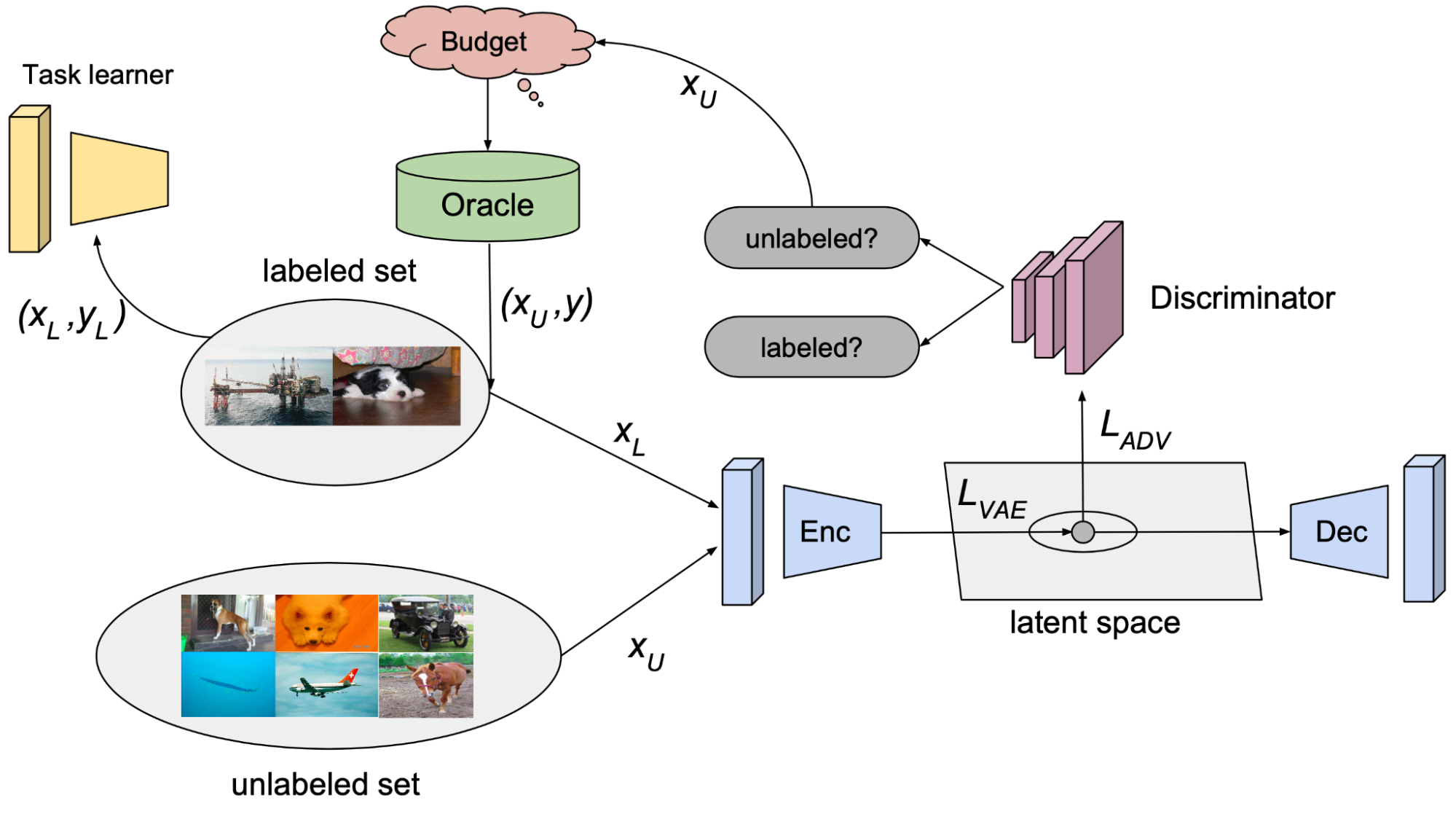
- The $\beta$-VAE learns a latent feature space $\mathbf{z}^l \cup \mathbf{z}^u$, for labeled and unlabeled data respectively, aiming to trick the discriminator $D(.)$ that all the data points are from the labeled pool;
- The discriminator $D(.)$ predicts whether a sample is labeled (1) or not (0) based on a latent representation $\mathbf{z}$. VAAL selects unlabeled samples with low discriminator scores, which indicates that those samples are sufficiently different from previously labeled ones.
The loss for VAE representation learning in VAAL contains both a reconstruction part (minimizing the ELBO of given samples) and an adversarial part (labeled and unlabeled data is drawn from the same probability distribution $q_\phi$):
where $p(\mathbf{\tilde{z}})$ is a unit Gaussian as a predefined prior and $\beta$ is the Lagrangian parameter.
The discriminator loss is:
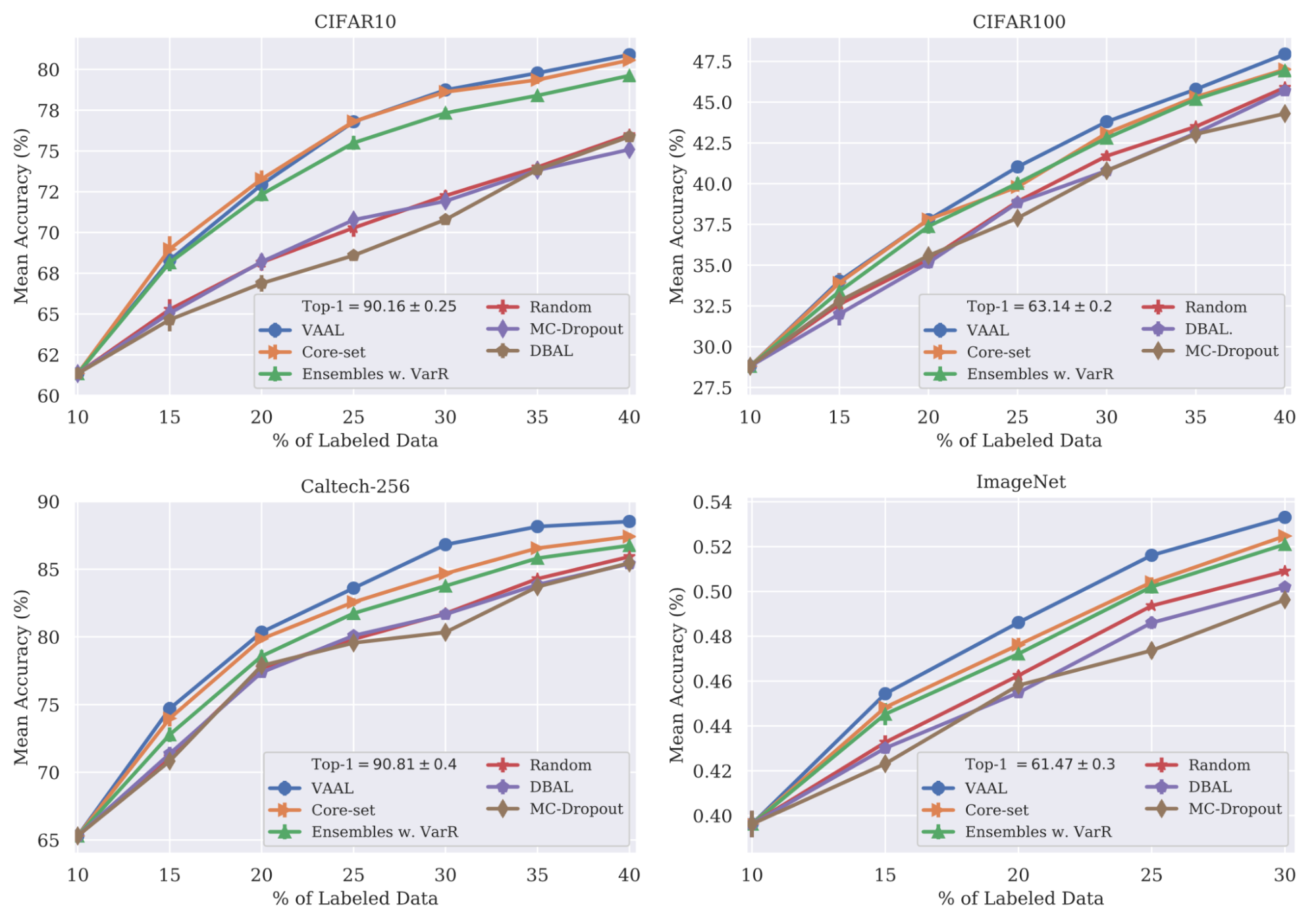
Ablation studies showed that jointly training VAE and discriminator is critical. Their results are robust to the biased initial labeled pool, different labeling budgets and noisy oracle.
MAL (Minimax Active Learning; Ebrahimiet al. 2021) is an extension of VAAL. The MAL framework consists of an entropy minimizing feature encoding network $F$ followed by an entropy maximizing classifier $C$. This minimax setup reduces the distribution gap between labeled and unlabeled data.
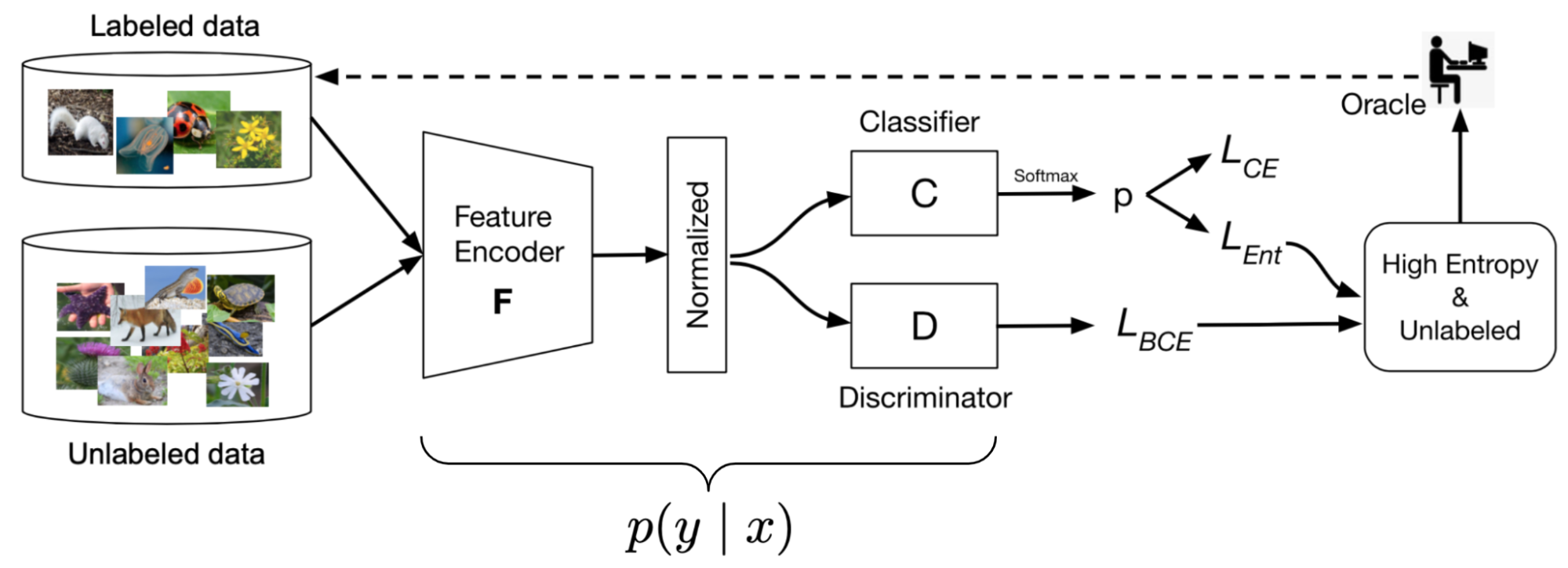
A feature encoder $F$ encodes a sample into a $\ell_2$-normalized $d$-dimensional latent vector. Assuming there are $K$ classes, a classifier $C$ is parameterized by $\mathbf{W} \in \mathbb{R}^{d \times K}$.
(1) First $F$ and $C$ are trained on labeled samples by a simple cross entropy loss to achieve good classification results,
(2) When training on the unlabeled examples, MAL relies on a minimax game setup
where,
- First, minimizing the entropy in $F$ encourages unlabeled samples associated with similar predicted labels to have similar features.
- Maximizing the entropy in $C$ adversarially makes the prediction to follow a more uniform class distribution. (My understanding here is that because the true label of an unlabeled sample is unknown, we should not optimize the classifier to maximize the predicted labels just yet.)
The discriminator is trained in the same way as in VAAL.
Sampling strategy in MAL considers both diversity and uncertainty:
- Diversity: the score of $D$ indicates how similar a sample is to previously seen examples. A score closer to 0 is better to select unfamiliar data points.
- Uncertainty: use the entropy obtained by $C$. A higher entropy score indicates that the model cannot make a confident prediction yet.
The experiments compared MAL to random, entropy, core-set, BALD and VAAL baselines, on image classification and segmentation tasks. The results look pretty strong.

CAL (Contrastive Active Learning; Margatina et al. 2021) intends to select contrastive examples. If two data points with different labels share similar network representations $\Phi(.)$, they are considered as contrastive examples in CAL. Given a pair of contrastive examples $(\mathbf{x}_i, \mathbf{x}_j)$, they should
Given an unlabeled sample $\mathbf{x}$, CAL runs the following process:
- Select the top $k$ nearest neighbors in the model feature space among the labeled samples, $\{(\mathbf{x}^l_i, y_i\}_{i=1}^M \subset \mathcal{X}$.
- Compute the KL divergence between the model output probabilities of $\mathbf{x}$ and each in $\{\mathbf{x}^l\}$. The contrastive score of $\mathbf{x}$ is the average of these KL divergence values: $s(\mathbf{x}) = \frac{1}{M} \sum_{i=1}^M \text{KL}(p(y \vert \mathbf{x}^l_i | p(y \vert \mathbf{x}))$.
- Samples with high contrastive scores are selected for active learning.
On a variety of classification tasks, the experiment results of CAL look similar to the entropy baseline.
Measuring Representativeness
Core-sets Approach
A core-set is a concept in computational geometry, referring to a small set of points that approximates the shape of a larger point set. Approximation can be captured by some geometric measure. In the active learning, we expect a model that is trained over the core-set to behave comparably with the model on the entire data points.
Sener & Savarese (2018) treats active learning as a core-set selection problem. Let’s say, there are $N$ samples in total accessible during training. During active learning, a small set of data points get labeled at every time step $t$, denoted as $\mathcal{S}^{(t)}$. The upper bound of the learning objective can be written as follows, where the core-set loss is defined as the difference between average empirical loss over the labeled samples and the loss over the entire dataset including unlabelled ones.
Then the active learning problem can be redefined as:
It is equivalent to the $k$-Center problem: choose $b$ center points such that the largest distance between a data point and its nearest center is minimized. This problem is NP-hard. An approximate solution depends on the greedy algorithm.
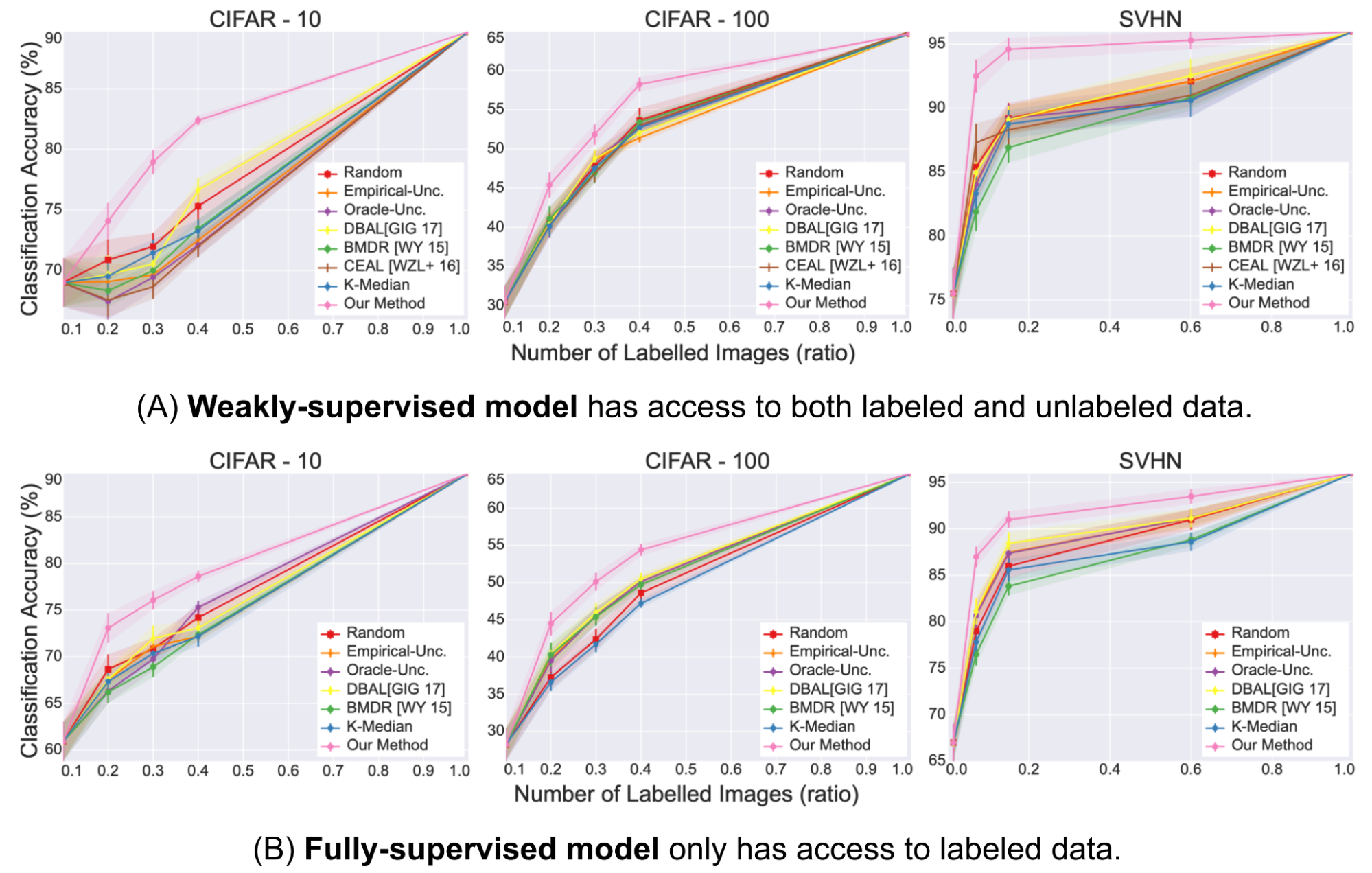
It works well on image classification tasks when there is a small number of classes. When the number of classes grows to be large or the data dimensionality increases (“curse of dimensionality”), the core-set method becomes less effective (Sinha et al. 2019).
Because the core-set selection is expensive, Coleman et al. (2020) experimented with a weaker model (e.g. smaller, weaker architecture, not fully trained) and found that empirically using a weaker model as a proxy can significantly shorten each repeated data selection cycle of training models and selecting samples, without hurting the final error much. Their method is referred to as SVP (Selection via Proxy).
Diverse Gradient Embedding
BADGE (Batch Active learning by Diverse Gradient Embeddings; Ash et al. 2020) tracks both model uncertainty and data diversity in the gradient space. Uncertainty is measured by the gradient magnitude w.r.t. the final layer of the network and diversity is captured by a diverse set of samples that span in the gradient space.
- Uncertainty. Given an unlabeled sample $\mathbf{x}$, BADGE first computes the prediction $\hat{y}$ and the gradient $g_\mathbf{x}$ of the loss on $(\mathbf{x}, \hat{y})$ w.r.t. the last layer’s parameters. They observed that the norm of $g_\mathbf{x}$ conservatively estimates the example’s influence on the model learning and high-confidence samples tend to have gradient embeddings of small magnitude.
- Diversity. Given many gradient embeddings of many samples, $g_\mathbf{x}$, BADGE runs $k$-means++ to sample data points accordingly.

Measuring Training Effects
Quantify Model Changes
Settles et al. (2008) introduced an active learning query strategy, named EGL (Expected Gradient Length). The motivation is to find samples that can trigger the greatest update on the model if their labels are known.
Let $\nabla \mathcal{L}(\theta)$ be the gradient of the loss function with respect to the model parameters. Specifically, given an unlabeled sample $\mathbf{x}_i$, we need to calculate the gradient assuming the label is $y \in \mathcal{Y}$, $\nabla \mathcal{L}^{(y)}(\theta)$. Because the true label $y_i$ is unknown, EGL relies on the current model belief to compute the expected gradient change:
BALD (Bayesian Active Learning by Disagreement; Houlsby et al. 2011) aims to identify samples to maximize the information gain about the model weights, that is equivalent to maximize the decrease in expected posterior entropy.
The underlying interpretation is to “seek $\mathbf{x}$ for which the model is marginally most uncertain about $y$ (high $H(y \vert \mathbf{x}, \mathcal{D})$), but for which individual settings of the parameters are confident (low $H(y \vert \mathbf{x}, \boldsymbol{\theta})$).” In other words, each individual posterior draw is confident but a collection of draws carry diverse opinions.
BALD was originally proposed for an individual sample and Kirsch et al. (2019) extended it to work in batch mode.
Forgetting Events
To investigate whether neural networks have a tendency to forget previously learned information, Mariya Toneva et al. (2019) designed an experiment: They track the model prediction for each sample during the training process and count the transitions for each sample from being classified correctly to incorrectly or vice-versa. Then samples can be categorized accordingly,
- Forgettable (redundant) samples: If the class label changes across training epochs.
- Unforgettable samples: If the class label assignment is consistent across training epochs. Those samples are never forgotten once learned.
They found that there are a large number of unforgettable examples that are never forgotten once learnt. Examples with noisy labels or images with “uncommon” features (visually complicated to classify) are among the most forgotten examples. The experiments empirically validated that unforgettable examples can be safely removed without compromising model performance.
In the implementation, the forgetting event is only counted when a sample is included in the current training batch; that is, they compute forgetting across presentations of the same example in subsequent mini-batches. The number of forgetting events per sample is quite stable across different seeds and forgettable examples have a small tendency to be first-time learned later in the training. The forgetting events are also found to be transferable throughout the training period and between architectures.
Forgetting events can be used as a signal for active learning acquisition if we hypothesize a model changing predictions during training is an indicator of model uncertainty. However, ground truth is unknown for unlabeled samples. Bengar et al. (2021) proposed a new metric called label dispersion for such a purpose. Let’s see across the training time, $c^*$ is the most commonly predicted label for the input $\mathbf{x}$ and the label dispersion measures the fraction of training steps when the model does not assign $c^**$ to this sample:
In their implementation, dispersion is computed at every epoch. Label dispersion is low if the model consistently assigns the same label to the same sample but high if the prediction changes often. Label dispersion is correlated with network uncertainty, as shown in 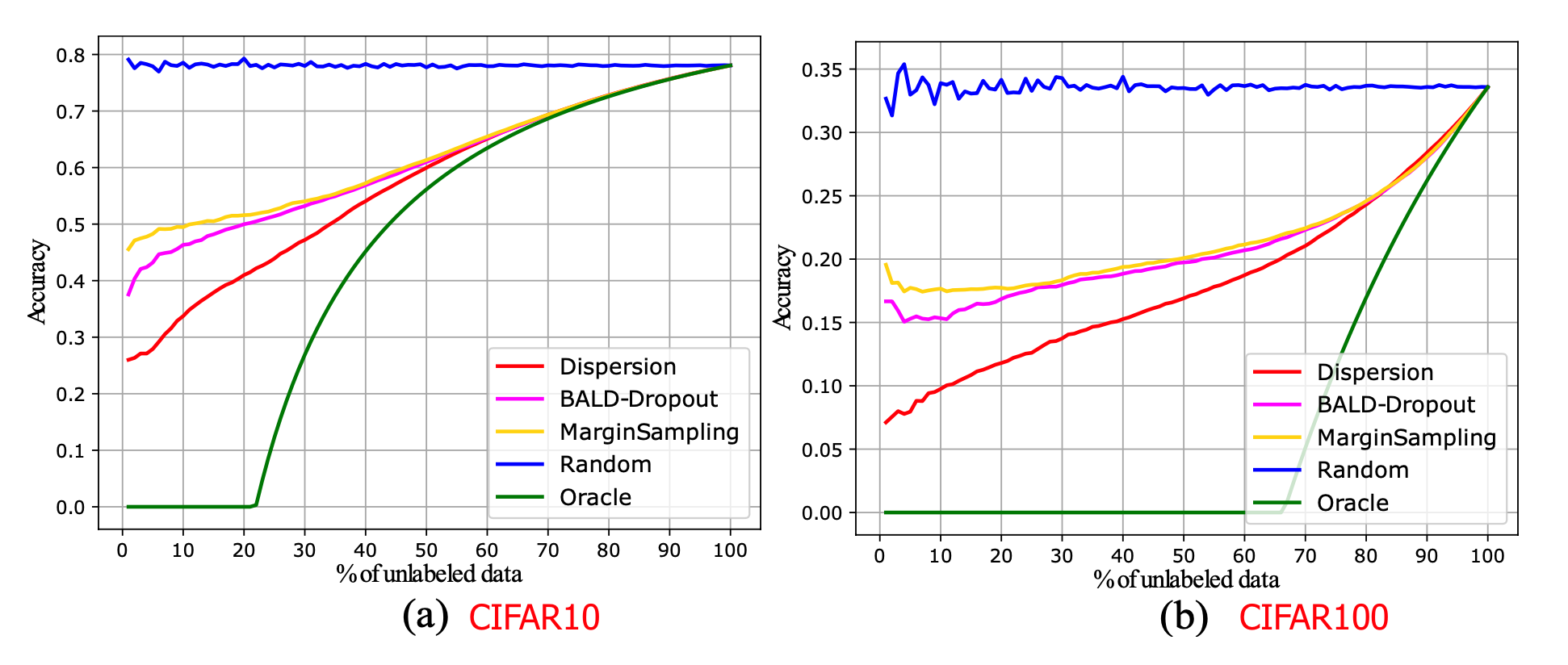
Hybrid
When running active learning in batch mode, it is important to control diversity within a batch. Suggestive Annotation (SA; Yang et al. 2017) is a two-step hybrid strategy, aiming to select both high uncertainty & highly representative labeled samples. It uses uncertainty obtained from an ensemble of models trained on the labeled data and core-sets for choosing representative data samples.
- First, SA selects top $K$ images with high uncertainty scores to form a candidate pool $\mathcal{S}_c \subseteq \mathcal{S}_U$. The uncertainty is measured as disagreement between multiple models training with bootstrapping.
- The next step is to find a subset $\mathcal{S}_a \subseteq \mathcal{S}_c$ with highest representativeness. The cosine similarity between feature vectors of two inputs approximates how similar they are. The representativeness of $\mathcal{S}_a$ for $\mathcal{S}_U$ reflects how well $\mathcal{S}_a$ can represent all the samples in $\mathcal{S}_u$, defined as:
Formulating $\mathcal{S}_a \subseteq \mathcal{S}_c$ with $k$ data points that maximizes $F(\mathcal{S}_a, \mathcal{S}_u)$ is a generalized version of the maximum set cover problem. It is NP-hard and its best possible polynomial time approximation algorithm is a simple greedy method.
- Initially, $\mathcal{S}_a = \emptyset$ and $F(\mathcal{S}_a, \mathcal{S}_u) = 0$.
- Then, iteratively add $\mathbf{x}_i \in \mathcal{S}_c$ that maximizes $F(\mathcal{S}_a \cup I_i, \mathcal{S}_u)$ over $\mathcal{S}_a$, until $\mathcal{S}_s$ contains $k$ images.
Zhdanov (2019) runs a similar process as SA, but at step 2, it relies on $k$-means instead of core-set, where the size of the candidate pool is configured relative to the batch size. Given batch size $b$ and a constant $beta$ (between 10 and 50), it follows these steps:
- Train a classifier on the labeled data;
- Measure informativeness of every unlabeled example (e.g. using uncertainty metrics);
- Prefilter top $\beta b \geq b$ most informative examples;
- Cluster $\beta b$ examples into $B$ clusters;
- Select $b$ different examples closest to the cluster centers for this round of active learning.
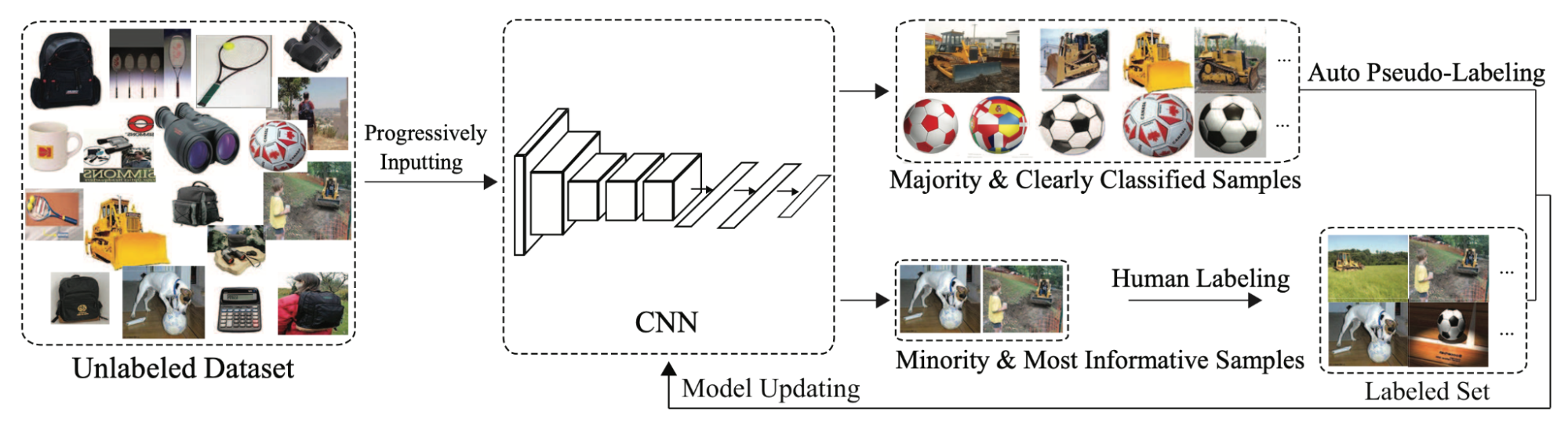
Active learning can be further combined with semi-supervised learning to save the budget. CEAL (Cost-Effective Active Learning; Yang et al. 2017) runs two things in parallel:
- Select uncertain samples via active learning and get them labeled;
- Select samples with the most confident prediction and assign them pseudo labels. The confidence prediction is judged by whether the prediction entropy is below a threshold $\delta$. As the model is getting better in time, the threshold $\delta$ decays in time as well.
Citation
Cited as:
Weng, Lilian. (Feb 2022). Learning with not enough data part 2: active learning. Lil’Log. https://lilianweng.github.io/posts/2022-02-20-active-learning/.
Or
@article{weng2022active,
title = "Learning with not Enough Data Part 2: Active Learning",
author = "Weng, Lilian",
journal = "lilianweng.github.io",
year = "2022",
month = "Feb",
url = "https://lilianweng.github.io/posts/2022-02-20-active-learning/"
}
References
[1] Burr Settles. Active learning literature survey. University of Wisconsin, Madison, 52(55-66):11, 2010.
[2] https://jacobgil.github.io/deeplearning/activelearning
[3] Yang et al. “Cost-effective active learning for deep image classification” TCSVT 2016.
[4] Yarin Gal et al. “Dropout as a Bayesian Approximation: representing model uncertainty in deep learning.” ICML 2016.
[5] Blundell et al. “Weight uncertainty in neural networks (Bayes-by-Backprop)” ICML 2015.
[6] Settles et al. “Multiple-Instance Active Learning.” NIPS 2007.
[7] Houlsby et al. Bayesian Active Learning for Classification and Preference Learning." arXiv preprint arXiv:1112.5745 (2020).
[8] Kirsch et al. “BatchBALD: Efficient and Diverse Batch Acquisition for Deep Bayesian Active Learning.” NeurIPS 2019.
[9] Beluch et al. “The power of ensembles for active learning in image classification.” CVPR 2018.
[10] Sener & Savarese. “Active learning for convolutional neural networks: A core-set approach.” ICLR 2018.
[11] Donggeun Yoo & In So Kweon. “Learning Loss for Active Learning.” CVPR 2019.
[12] Margatina et al. “Active Learning by Acquiring Contrastive Examples.” EMNLP 2021.
[13] Sinha et al. “Variational Adversarial Active Learning” ICCV 2019
[14] Ebrahimiet al. “Minmax Active Learning” arXiv preprint arXiv:2012.10467 (2021).
[15] Mariya Toneva et al. “An empirical study of example forgetting during deep neural network learning.” ICLR 2019.
[16] Javad Zolfaghari Bengar et al. “When Deep Learners Change Their Mind: Learning Dynamics for Active Learning.” CAIP 2021.
[17] Yang et al. “Suggestive annotation: A deep active learning framework for biomedical image segmentation.” MICCAI 2017.
[18] Fedor Zhdanov. “Diverse mini-batch Active Learning” arXiv preprint arXiv:1901.05954 (2019).