[Updated on 2018-12-20: Remove YOLO here. Part 4 will cover multiple fast object detection algorithms, including YOLO.]
[Updated on 2018-12-27: Add bbox regression and tricks sections for R-CNN.]

In the series of “Object Detection for Dummies”, we started with basic concepts in image processing, such as gradient vectors and HOG, in Part 1. Then we introduced classic convolutional neural network architecture designs for classification and pioneer models for object recognition, Overfeat and DPM, in Part 2. In the third post of this series, we are about to review a set of models in the R-CNN (“Region-based CNN”) family.

Links to all the posts in the series: [Part 1] [Part 2] [Part 3] [Part 4].

Here is a list of papers covered in this post ;)

Model Goal Resources
R-CNN Object recognition [paper][code]
Fast R-CNN Object recognition [paper][code]
Faster R-CNN Object recognition [paper][code]
Mask R-CNN Image segmentation [paper][code]

R-CNN

R-CNN (Girshick et al., 2014) is short for “Region-based Convolutional Neural Networks”. The main idea is composed of two steps. First, using selective search, it identifies a manageable number of bounding-box object region candidates (“region of interest” or “RoI”). And then it extracts CNN features from each region independently for classification.

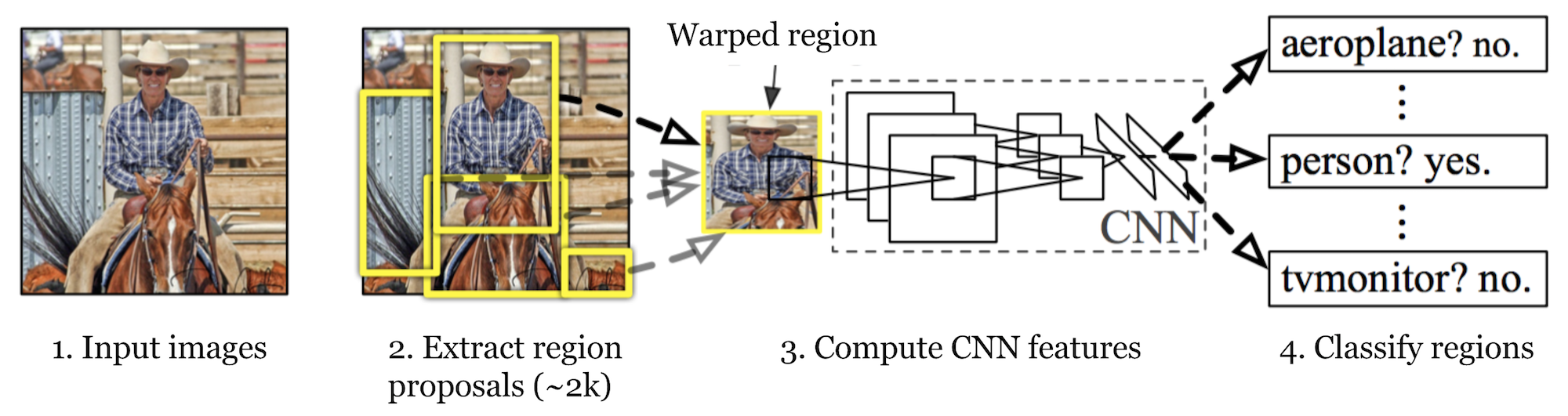
Fig. 1. The architecture of R-CNN. (Image source: Girshick et al., 2014)

Model Workflow

How R-CNN works can be summarized as follows:

  1. Pre-train a CNN network on image classification tasks; for example, VGG or ResNet trained on ImageNet dataset. The classification task involves N classes.

NOTE: You can find a pre-trained AlexNet in Caffe Model Zoo. I don’t think you can find it in Tensorflow, but Tensorflow-slim model library provides pre-trained ResNet, VGG, and others.

  1. Propose category-independent regions of interest by selective search (~2k candidates per image). Those regions may contain target objects and they are of different sizes.
  2. Region candidates are warped to have a fixed size as required by CNN.
  3. Continue fine-tuning the CNN on warped proposal regions for K + 1 classes; The additional one class refers to the background (no object of interest). In the fine-tuning stage, we should use a much smaller learning rate and the mini-batch oversamples the positive cases because most proposed regions are just background.
  4. Given every image region, one forward propagation through the CNN generates a feature vector. This feature vector is then consumed by a binary SVM trained for each class independently.
    The positive samples are proposed regions with IoU (intersection over union) overlap threshold >= 0.3, and negative samples are irrelevant others.
  5. To reduce the localization errors, a regression model is trained to correct the predicted detection window on bounding box correction offset using CNN features.

Bounding Box Regression

Given a predicted bounding box coordinate $\mathbf{p} = (p_x, p_y, p_w, p_h)$ (center coordinate, width, height) and its corresponding ground truth box coordinates $\mathbf{g} = (g_x, g_y, g_w, g_h)$ , the regressor is configured to learn scale-invariant transformation between two centers and log-scale transformation between widths and heights. All the transformation functions take $\mathbf{p}$ as input.

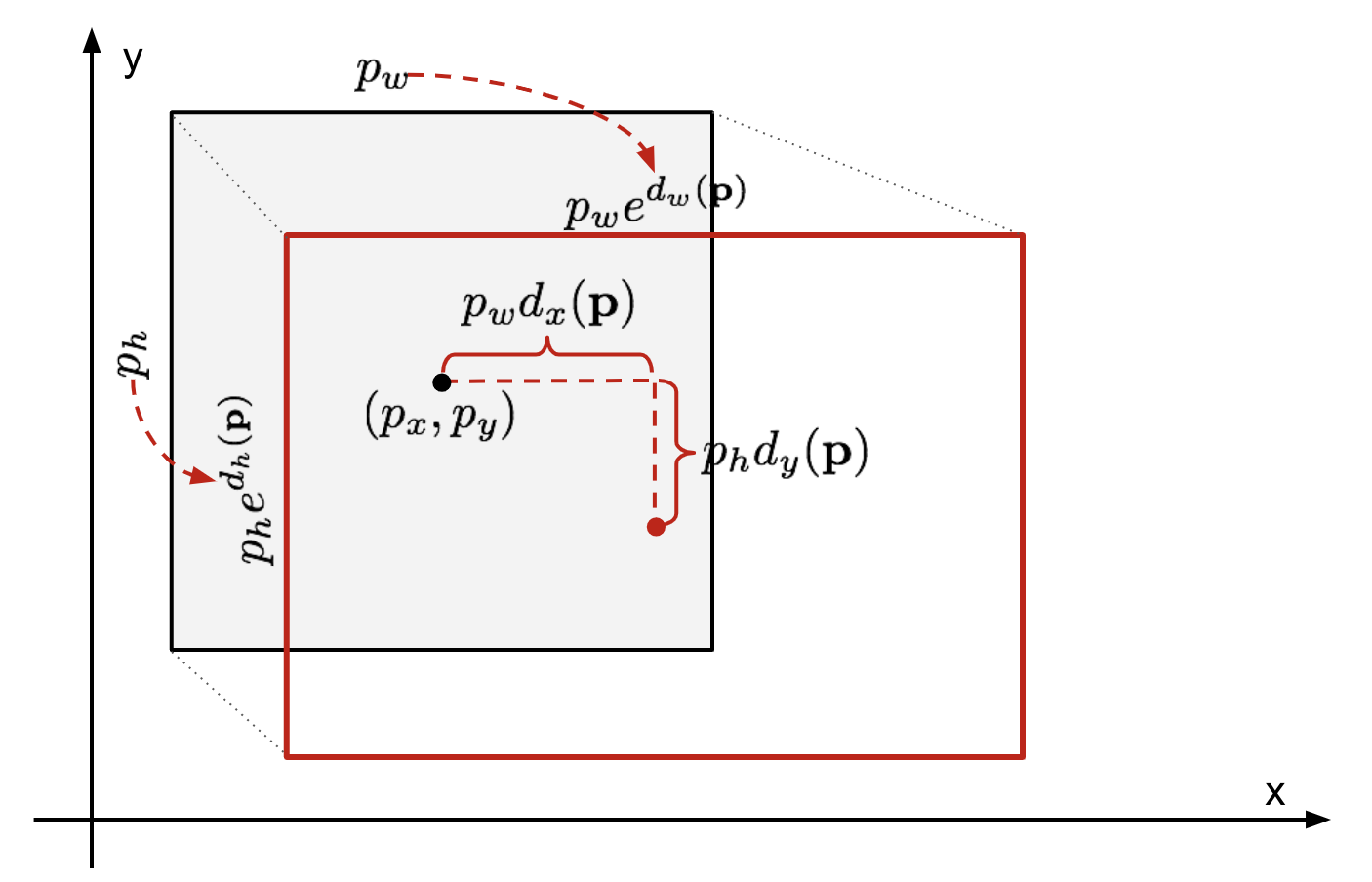
$$ \begin{aligned} \hat{g}_x &= p_w d_x(\mathbf{p}) + p_x \\ \hat{g}_y &= p_h d_y(\mathbf{p}) + p_y \\ \hat{g}_w &= p_w \exp({d_w(\mathbf{p})}) \\ \hat{g}_h &= p_h \exp({d_h(\mathbf{p})}) \end{aligned} $$
Fig. 2. Illustration of transformation between predicted and ground truth bounding boxes.

An obvious benefit of applying such transformation is that all the bounding box correction functions, $d_i(\mathbf{p})$ where $i \in \{ x, y, w, h \}$, can take any value between [-∞, +∞]. The targets for them to learn are:

$$ \begin{aligned} t_x &= (g_x - p_x) / p_w \\ t_y &= (g_y - p_y) / p_h \\ t_w &= \log(g_w/p_w) \\ t_h &= \log(g_h/p_h) \end{aligned} $$

A standard regression model can solve the problem by minimizing the SSE loss with regularization:

$$ \mathcal{L}_\text{reg} = \sum_{i \in \{x, y, w, h\}} (t_i - d_i(\mathbf{p}))^2 + \lambda \|\mathbf{w}\|^2 $$

The regularization term is critical here and RCNN paper picked the best λ by cross validation. It is also noteworthy that not all the predicted bounding boxes have corresponding ground truth boxes. For example, if there is no overlap, it does not make sense to run bbox regression. Here, only a predicted box with a nearby ground truth box with at least 0.6 IoU is kept for training the bbox regression model.

Common Tricks

Several tricks are commonly used in RCNN and other detection models.

Non-Maximum Suppression

Likely the model is able to find multiple bounding boxes for the same object. Non-max suppression helps avoid repeated detection of the same instance. After we get a set of matched bounding boxes for the same object category: Sort all the bounding boxes by confidence score. Discard boxes with low confidence scores. While there is any remaining bounding box, repeat the following: Greedily select the one with the highest score. Skip the remaining boxes with high IoU (i.e. > 0.5) with previously selected one.

Fig. 3. Multiple bounding boxes detect the car in the image. After non-maximum suppression, only the best remains and the rest are ignored as they have large overlaps with the selected one. (Image source: DPM paper)

Hard Negative Mining

We consider bounding boxes without objects as negative examples. Not all the negative examples are equally hard to be identified. For example, if it holds pure empty background, it is likely an “easy negative”; but if the box contains weird noisy texture or partial object, it could be hard to be recognized and these are “hard negative”.

The hard negative examples are easily misclassified. We can explicitly find those false positive samples during the training loops and include them in the training data so as to improve the classifier.

Speed Bottleneck

Looking through the R-CNN learning steps, you could easily find out that training an R-CNN model is expensive and slow, as the following steps involve a lot of work:

  • Running selective search to propose 2000 region candidates for every image;
  • Generating the CNN feature vector for every image region (N images * 2000).
  • The whole process involves three models separately without much shared computation: the convolutional neural network for image classification and feature extraction; the top SVM classifier for identifying target objects; and the regression model for tightening region bounding boxes.

Fast R-CNN

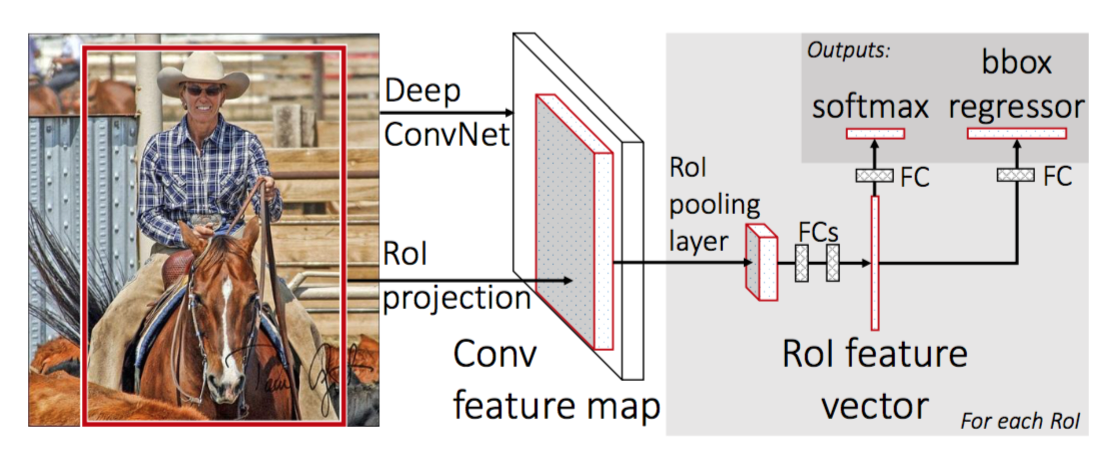
To make R-CNN faster, Girshick (2015) improved the training procedure by unifying three independent models into one jointly trained framework and increasing shared computation results, named Fast R-CNN. Instead of extracting CNN feature vectors independently for each region proposal, this model aggregates them into one CNN forward pass over the entire image and the region proposals share this feature matrix. Then the same feature matrix is branched out to be used for learning the object classifier and the bounding-box regressor. In conclusion, computation sharing speeds up R-CNN.

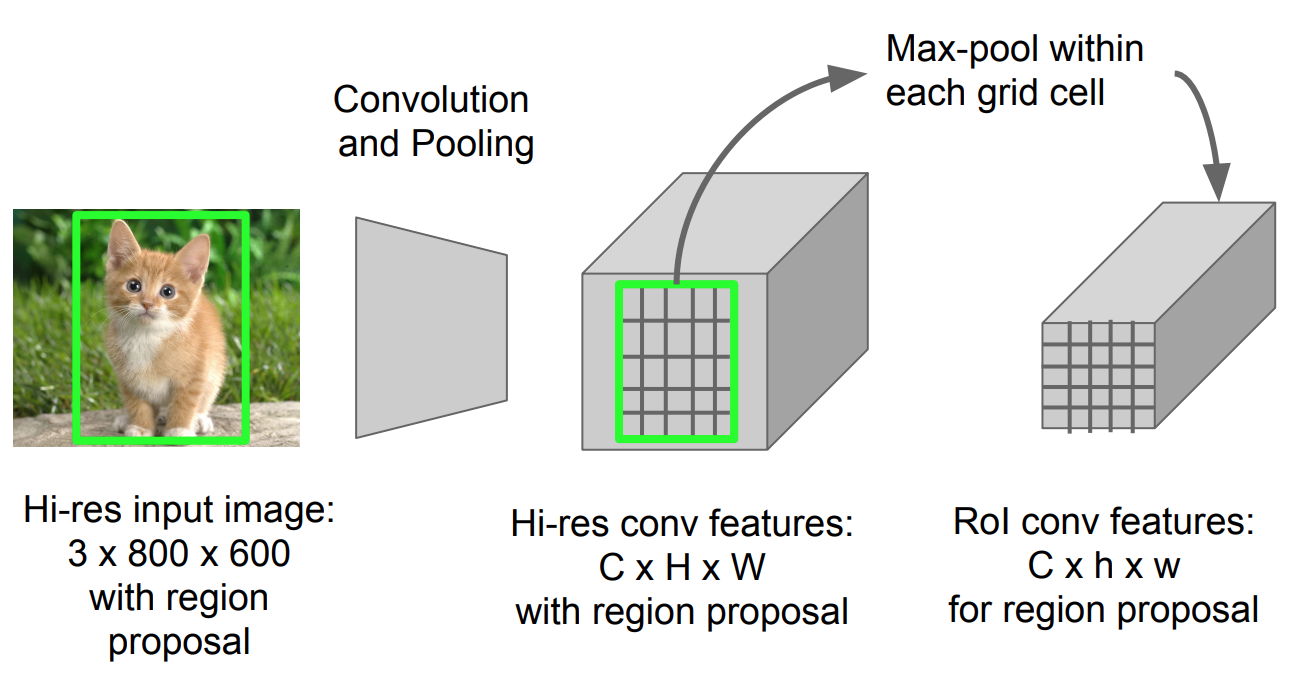
Fig. 4. The architecture of Fast R-CNN. (Image source: Girshick, 2015)

RoI Pooling

It is a type of max pooling to convert features in the projected region of the image of any size, h x w, into a small fixed window, H x W. The input region is divided into H x W grids, approximately every subwindow of size h/H x w/W. Then apply max-pooling in each grid.

Fig. 5. RoI pooling (Image source: Stanford CS231n slides.)

Model Workflow

How Fast R-CNN works is summarized as follows; many steps are same as in R-CNN:

  1. First, pre-train a convolutional neural network on image classification tasks.
  2. Propose regions by selective search (~2k candidates per image).
  3. Alter the pre-trained CNN:
    • Replace the last max pooling layer of the pre-trained CNN with a RoI pooling layer. The RoI pooling layer outputs fixed-length feature vectors of region proposals. Sharing the CNN computation makes a lot of sense, as many region proposals of the same images are highly overlapped.
    • Replace the last fully connected layer and the last softmax layer (K classes) with a fully connected layer and softmax over K + 1 classes.
  4. Finally the model branches into two output layers:
    • A softmax estimator of K + 1 classes (same as in R-CNN, +1 is the “background” class), outputting a discrete probability distribution per RoI.
    • A bounding-box regression model which predicts offsets relative to the original RoI for each of K classes.

Loss Function

The model is optimized for a loss combining two tasks (classification + localization):

| Symbol | Explanation | | $u$ | True class label, $ u \in 0, 1, \dots, K$; by convention, the catch-all background class has $u = 0$. | | $p$ | Discrete probability distribution (per RoI) over K + 1 classes: $p = (p_0, \dots, p_K)$, computed by a softmax over the K + 1 outputs of a fully connected layer. | | $v$ | True bounding box $ v = (v_x, v_y, v_w, v_h) $. | | $t^u$ | Predicted bounding box correction, $t^u = (t^u_x, t^u_y, t^u_w, t^u_h)$. See above. | {:.info}

The loss function sums up the cost of classification and bounding box prediction: $\mathcal{L} = \mathcal{L}_\text{cls} + \mathcal{L}_\text{box}$. For “background” RoI, $\mathcal{L}_\text{box}$ is ignored by the indicator function $\mathbb{1} [u \geq 1]$, defined as:

$$ \mathbb{1} [u >= 1] = \begin{cases} 1 & \text{if } u \geq 1\\ 0 & \text{otherwise} \end{cases} $$

The overall loss function is:

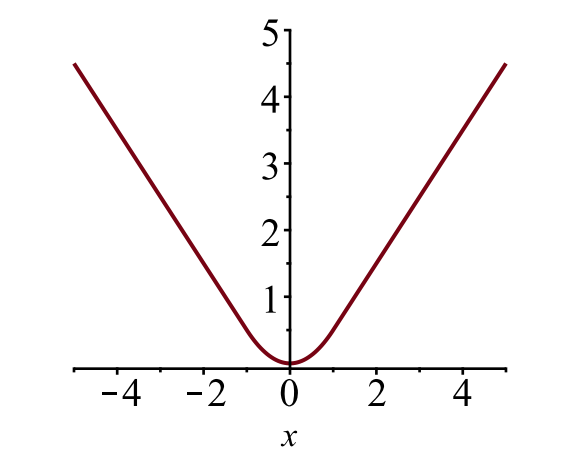
$$ \begin{align*} \mathcal{L}(p, u, t^u, v) &= \mathcal{L}_\text{cls} (p, u) + \mathbb{1} [u \geq 1] \mathcal{L}_\text{box}(t^u, v) \\ \mathcal{L}_\text{cls}(p, u) &= -\log p_u \\ \mathcal{L}_\text{box}(t^u, v) &= \sum_{i \in \{x, y, w, h\}} L_1^\text{smooth} (t^u_i - v_i) \end{align*} $$

The bounding box loss $\mathcal{L}_{box}$ should measure the difference between $t^u_i$ and $v_i$ using a robust loss function. The smooth L1 loss is adopted here and it is claimed to be less sensitive to outliers.

$$ L_1^\text{smooth}(x) = \begin{cases} 0.5 x^2 & \text{if } \vert x \vert < 1\\ \vert x \vert - 0.5 & \text{otherwise} \end{cases} $$
Fig. 6. The plot of smooth L1 loss, $y = L\_1^\text{smooth}(x)$. (Image source: link)

Speed Bottleneck

Fast R-CNN is much faster in both training and testing time. However, the improvement is not dramatic because the region proposals are generated separately by another model and that is very expensive.

Faster R-CNN

An intuitive speedup solution is to integrate the region proposal algorithm into the CNN model. Faster R-CNN (Ren et al., 2016) is doing exactly this: construct a single, unified model composed of RPN (region proposal network) and fast R-CNN with shared convolutional feature layers.

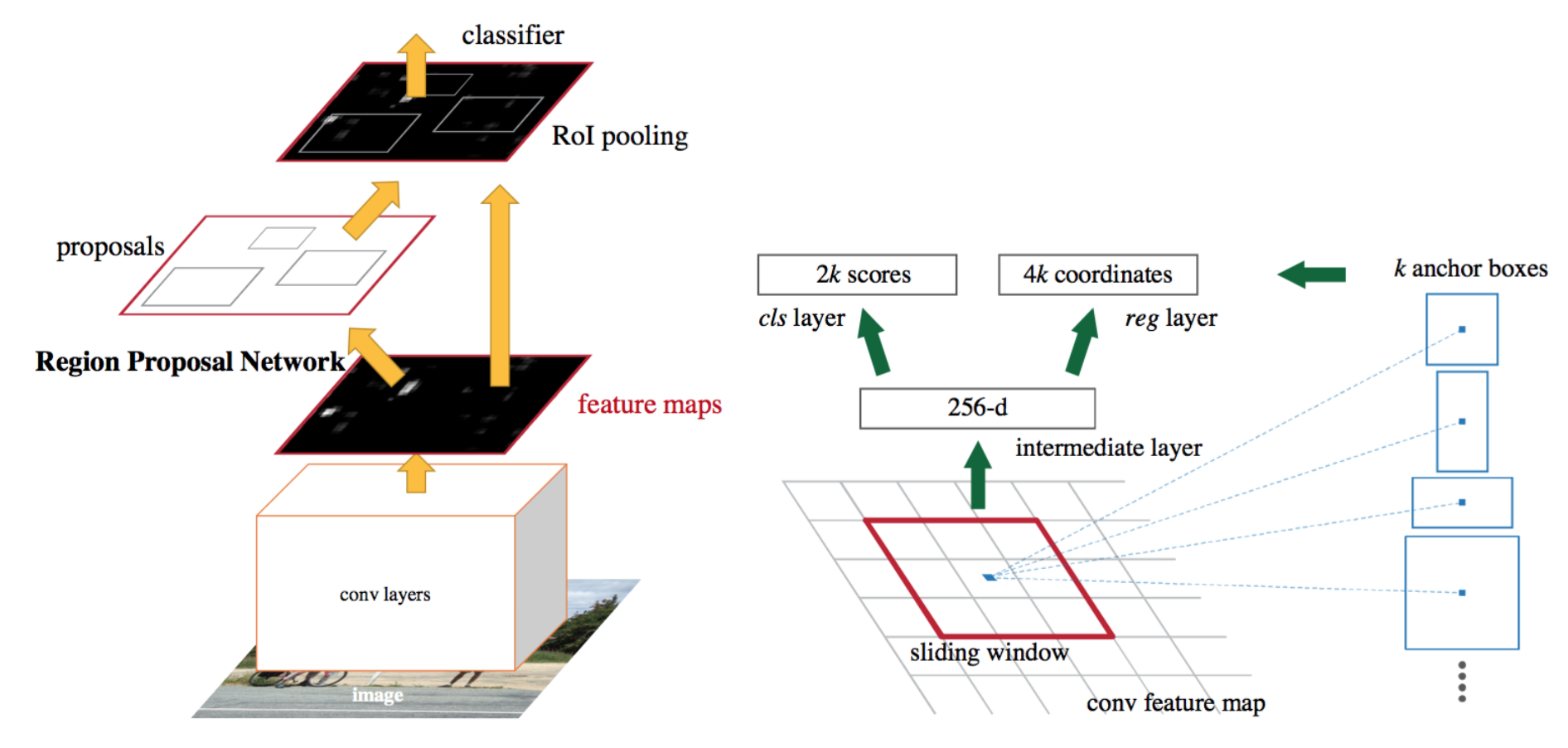
Fig. 7. An illustration of Faster R-CNN model. (Image source: Ren et al., 2016)

Model Workflow

  1. Pre-train a CNN network on image classification tasks.
  2. Fine-tune the RPN (region proposal network) end-to-end for the region proposal task, which is initialized by the pre-train image classifier. Positive samples have IoU (intersection-over-union) > 0.7, while negative samples have IoU < 0.3.
    • Slide a small n x n spatial window over the conv feature map of the entire image.
    • At the center of each sliding window, we predict multiple regions of various scales and ratios simultaneously. An anchor is a combination of (sliding window center, scale, ratio). For example, 3 scales + 3 ratios => k=9 anchors at each sliding position.
  3. Train a Fast R-CNN object detection model using the proposals generated by the current RPN
  4. Then use the Fast R-CNN network to initialize RPN training. While keeping the shared convolutional layers, only fine-tune the RPN-specific layers. At this stage, RPN and the detection network have shared convolutional layers!
  5. Finally fine-tune the unique layers of Fast R-CNN
  6. Step 4-5 can be repeated to train RPN and Fast R-CNN alternatively if needed.

Loss Function

Faster R-CNN is optimized for a multi-task loss function, similar to fast R-CNN.

| Symbol | Explanation | | $p_i$ | Predicted probability of anchor i being an object. | | $p^*_i$ | Ground truth label (binary) of whether anchor i is an object. | | $t_i$ | Predicted four parameterized coordinates. | | $t^*_i$ | Ground truth coordinates. | | $N_\text{cls}$ | Normalization term, set to be mini-batch size (~256) in the paper. | | $N_\text{box}$ | Normalization term, set to the number of anchor locations (~2400) in the paper. | | $\lambda$ | A balancing parameter, set to be ~10 in the paper (so that both $\mathcal{L}_\text{cls}$ and $\mathcal{L}_\text{box}$ terms are roughly equally weighted). | {:.info}

The multi-task loss function combines the losses of classification and bounding box regression:

$$ \begin{align*} \mathcal{L} &= \mathcal{L}_\text{cls} + \mathcal{L}_\text{box} \\ \mathcal{L}(\{p_i\}, \{t_i\}) &= \frac{1}{N_\text{cls}} \sum_i \mathcal{L}_\text{cls} (p_i, p^*_i) + \frac{\lambda}{N_\text{box}} \sum_i p^*_i \cdot L_1^\text{smooth}(t_i - t^*_i) \\ \end{align*} $$

where $\mathcal{L}_\text{cls}$ is the log loss function over two classes, as we can easily translate a multi-class classification into a binary classification by predicting a sample being a target object versus not. $L_1^\text{smooth}$ is the smooth L1 loss.

$$ \mathcal{L}_\text{cls} (p_i, p^*_i) = - p^*_i \log p_i - (1 - p^*_i) \log (1 - p_i) $$

Mask R-CNN

Mask R-CNN (He et al., 2017) extends Faster R-CNN to pixel-level image segmentation. The key point is to decouple the classification and the pixel-level mask prediction tasks. Based on the framework of Faster R-CNN, it added a third branch for predicting an object mask in parallel with the existing branches for classification and localization. The mask branch is a small fully-connected network applied to each RoI, predicting a segmentation mask in a pixel-to-pixel manner.

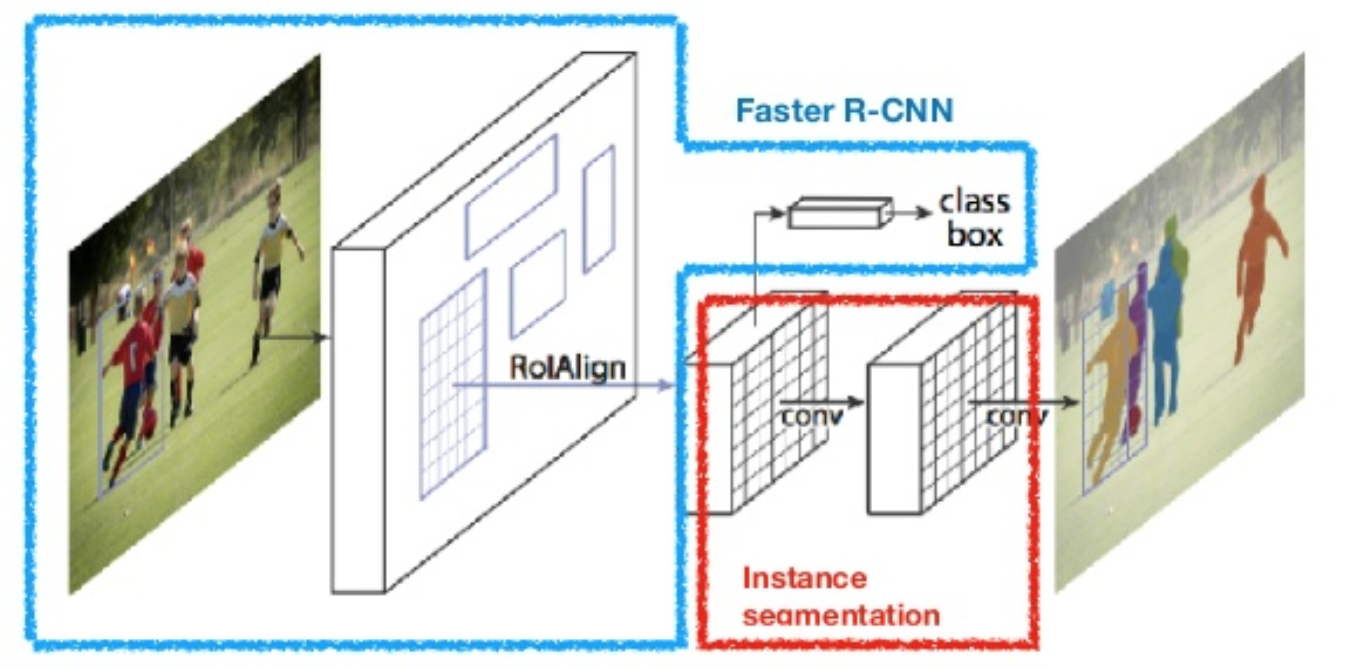
Fig. 8. Mask R-CNN is Faster R-CNN model with image segmentation. (Image source: He et al., 2017)

Because pixel-level segmentation requires much more fine-grained alignment than bounding boxes, mask R-CNN improves the RoI pooling layer (named “RoIAlign layer”) so that RoI can be better and more precisely mapped to the regions of the original image.

Fig. 9. Predictions by Mask R-CNN on COCO test set. (Image source: He et al., 2017)

RoIAlign

The RoIAlign layer is designed to fix the location misalignment caused by quantization in the RoI pooling. RoIAlign removes the hash quantization, for example, by using x/16 instead of [x/16], so that the extracted features can be properly aligned with the input pixels. Bilinear interpolation is used for computing the floating-point location values in the input.

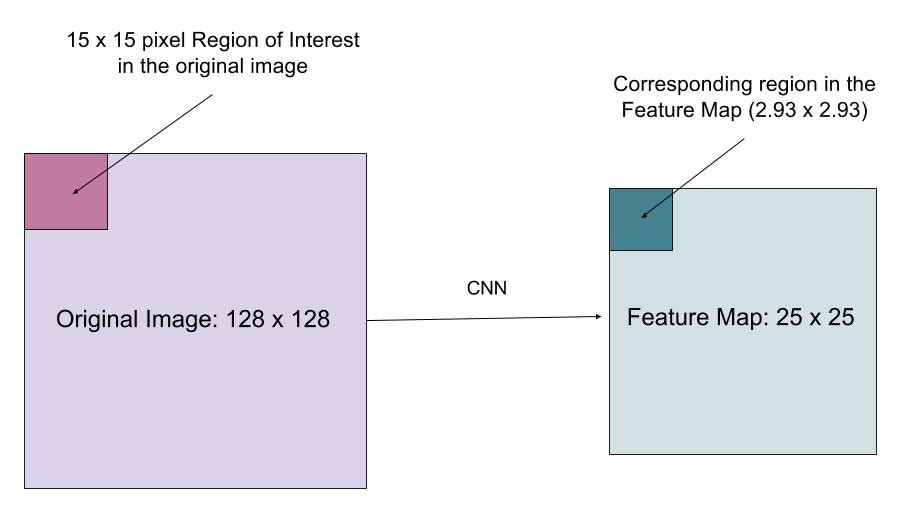
Fig. 10. A region of interest is mapped **accurately** from the original image onto the feature map without rounding up to integers. (Image source: link)

Loss Function

The multi-task loss function of Mask R-CNN combines the loss of classification, localization and segmentation mask: $ \mathcal{L} = \mathcal{L}_\text{cls} + \mathcal{L}_\text{box} + \mathcal{L}_\text{mask}$, where $\mathcal{L}_\text{cls}$ and $\mathcal{L}_\text{box}$ are same as in Faster R-CNN.

The mask branch generates a mask of dimension m x m for each RoI and each class; K classes in total. Thus, the total output is of size $K \cdot m^2$. Because the model is trying to learn a mask for each class, there is no competition among classes for generating masks.

$\mathcal{L}_\text{mask}$ is defined as the average binary cross-entropy loss, only including k-th mask if the region is associated with the ground truth class k.

$$ \mathcal{L}_\text{mask} = - \frac{1}{m^2} \sum_{1 \leq i, j \leq m} \big[ y_{ij} \log \hat{y}^k_{ij} + (1-y_{ij}) \log (1- \hat{y}^k_{ij}) \big] $$

where $y_{ij}$ is the label of a cell (i, j) in the true mask for the region of size m x m; $\hat{y}_{ij}^k$ is the predicted value of the same cell in the mask learned for the ground-truth class k.

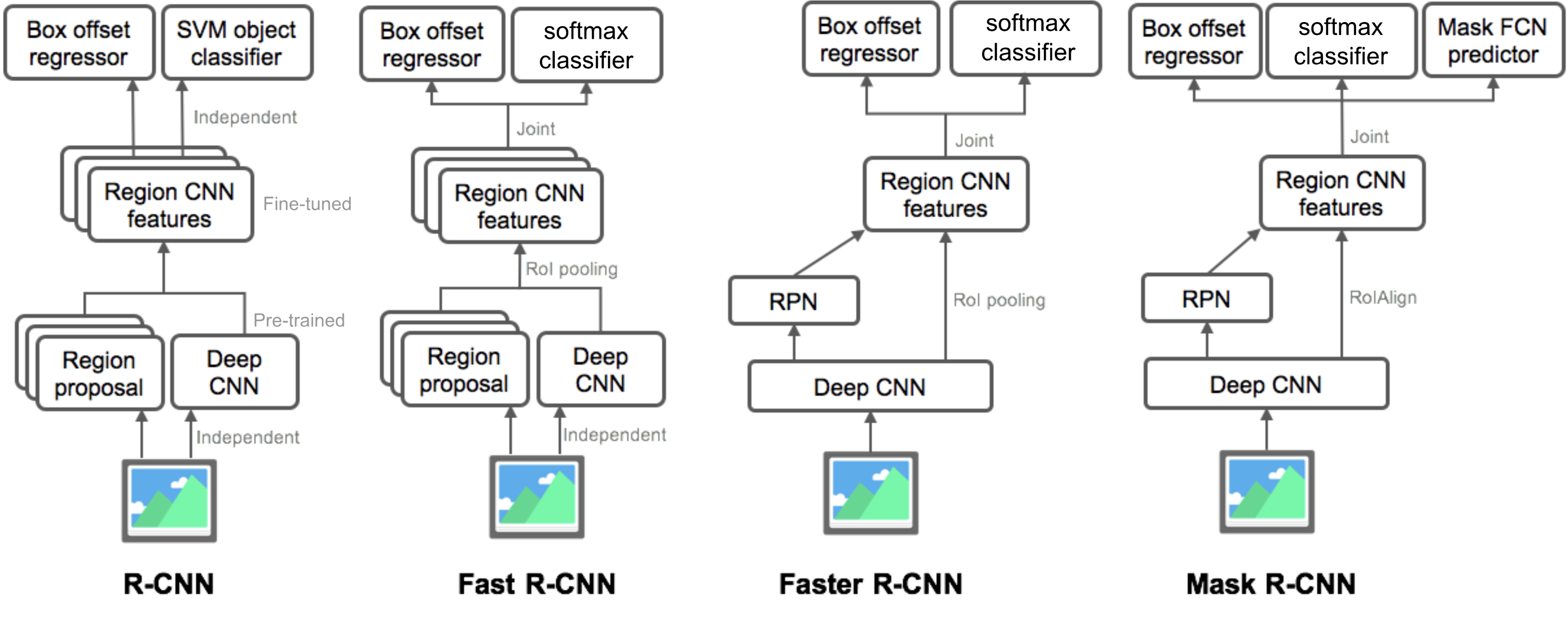
Summary of Models in the R-CNN family

Here I illustrate model designs of R-CNN, Fast R-CNN, Faster R-CNN and Mask R-CNN. You can track how one model evolves to the next version by comparing the small differences.

Cited as:

@article{weng2017detection3,
  title   = "Object Detection for Dummies Part 3: R-CNN Family",
  author  = "Weng, Lilian",
  journal = "lilianweng.github.io",
  year    = "2017",
  url     = "https://lilianweng.github.io/posts/2017-12-31-object-recognition-part-3/"
}

Reference

[1] Ross Girshick, Jeff Donahue, Trevor Darrell, and Jitendra Malik. “Rich feature hierarchies for accurate object detection and semantic segmentation.” In Proc. IEEE Conf. on computer vision and pattern recognition (CVPR), pp. 580-587. 2014.

[2] Ross Girshick. “Fast R-CNN.” In Proc. IEEE Intl. Conf. on computer vision, pp. 1440-1448. 2015.

[3] Shaoqing Ren, Kaiming He, Ross Girshick, and Jian Sun. “Faster R-CNN: Towards real-time object detection with region proposal networks.” In Advances in neural information processing systems (NIPS), pp. 91-99. 2015.

[4] Kaiming He, Georgia Gkioxari, Piotr Dollár, and Ross Girshick. “Mask R-CNN.” arXiv preprint arXiv:1703.06870, 2017.

[5] Joseph Redmon, Santosh Divvala, Ross Girshick, and Ali Farhadi. “You only look once: Unified, real-time object detection.” In Proc. IEEE Conf. on computer vision and pattern recognition (CVPR), pp. 779-788. 2016.

[6] “A Brief History of CNNs in Image Segmentation: From R-CNN to Mask R-CNN” by Athelas.

[7] Smooth L1 Loss: https://github.com/rbgirshick/py-faster-rcnn/files/764206/SmoothL1Loss.1.pdf